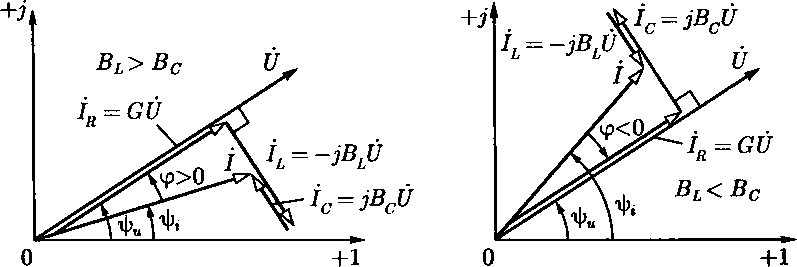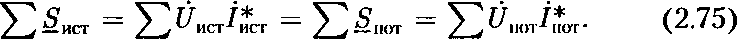КАТУШКА С МАГНИТОПРОВОДОМ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 9 страница

Величина, обратная комплексной проводимости 1/Y=Z = Ze™ — это комплексное сопротивление. Поэтому в показательной форме комплексная проводимость

=Ye'™

~ Z Ze"

и в тригонометрической форме

Y = Усовф —jY втф,

где У =|У|=yjG²+ (B_L- В_СУ

сти цепи или полная проводимость цепи; ф = arctg ¹ —-

G

мент комплексной проводимости цепи.

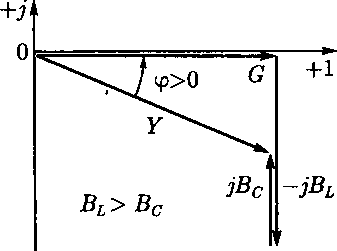
На комплексной плоскости (рис. 2.33) слагаемые комплексной проводимости цепи изображены в виде векторов для двух случаев: B_L> В_с(рис. 2.33, а) и В_ь< В_с(рис. 2.33, б). В первом случае ком­плексная проводимость цепи имеет индуктивный характер, во вто­ром — емкостный.

(2.64)

Подставив значение комплексной проводимости цепи в показа­тельной форме (2.63) в (2.61), получим комплексное значение тока в виде

I = iefti = YE = YU = Ft/e^"^.

Из (2.64) следует, что действующее значение тока в неразветв­ленной части цепи

/ = yjG²+ {B_L- S_c)²t/.

(2.63а)

(2.636)

модуль комплексной проводимо- аргу-

На рис. 2.34 приведены векторные диаграммы напряжения и то­ков рассматриваемой цепи для двух случаев:B_L> В_с (рис. 2.34, а) и < В^(рис. 2.34, б) при одинаковом напряжении С/ = J7Zo|v Если комплексная проводимость цепи имеет индуктивный характер, то

BL<BC		чвс
У >
	G
б		+ , 1—''

+j

 

общий ток (в неразветвленной части цепи) отстает по фазе от на­пряжения, так как ф > О, т.е. я|;_м>i|vЕсли комплексная проводи­мость цепи имеет емкостный характер, то общий ток опережает по фазе напряжение, гак как ф < 0, т.е. я|;_и< Заметим (см. рис. 2.25), что положительные значения угла ф отсчитываются против направ­ления движения стрелки часов от вектора комплексного значения тока /.

Комплексная мощность параллельного соединения пассивных элементов равна комплексной мощности источника ЭДС:

s = ui* = [/(/* + /* + /*) - GU² + jB_LU²- jB_cU² = = Y*U²= P + j(Q_L+ Q_c) =P + jQ.

Если включены параллельно несколько резистивных, индуктив­ных и емкостных элементов, то комплексная проводимость

¥.= =£<?"JE^ + =

= Х> ~ З{Е^вь ~Y,^BC)=^g~ JB.                (2-65)

гдеG = У^д— активная проводимость цепи\ В = ^B_L— У~]В_С — реактивная проводимость цепи. Такие названия проводимостей даны по аналогии с названиями сопротивлений для неразветвленной цепи [см. (2.48)].

Введенные здесь понятия об активной и реактивной проводимо- стях цепи применяются и для характеристики пассивных двухпо­люсников.

Рис. 2.34

а                                               б

Выражению (2.65) соответствуют треугольники проводимостей на комплексной плоскости (рис. 2.35, а, б). Из треугольников про­водимостей и из (2.65) следуют тригонометрическая и показатель­ная формы комплексной проводимости цепи при произвольном чис­ле параллельных ветвей с резистивными, индуктивными и емкост-

	в> 0			+г		В< 0
	/ф> 0	G	+1			W		-зВ
Г			-зВ		<3-
Gu		У				'СсрСО	G
				0	+1

 

Рис. 2.35

(2.66а)

(2.666)

ными элементами, совпадающие с (2.63), причем полная проводи­мость

у = yjG²+ В²

и аргумент

, в

Ч> =arctg-.

В общем случае параллельные ветви могут содержать последова­тельные соединения резистивных, индуктивных и емкостных элемен­тов. Комплексная проводимость цепи с параллельным соединением п таких ветвей равна сумме комплексных проводимостей всех ветвей:

Z = = = + + - + r⁺ "⁺

к=1    к=1 —к йл —2            Ак       ±Ln

где У_к иZ_k— комплексные проводимость и сопротивление к-й ветви.

2.16. Активная, реактивная, комплексная и полная проводимости пассивного двухполюсника

+3 о

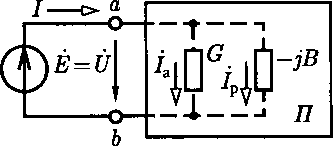
Выше (см. 2.12) пассивный двухполюсник был представлен эк­вивалентной схемой замещения, состоящей из последовательного со­единения элементов с активным и реактивным сопротивлениями (см. рис. 2.27). Однако решение многих задач будет проще, если пас­сивный двухполюсник представить дру­гой эквивалентной схемой, состоящей из параллельного соединения элементов с активной и реактивной проводимостями (рис. 2.36). Параметром такого пассив­ного двухполюсника является его вход­ная комплексная проводимость между Рис. 2.36 выводами а и Ь:

Y = i = -i = Ye~* = Г совф - jTsimp =G - jB,(2.67)

U E

гдеU = U Z'ф_и = £'и/ = //'ф. — комплексные значения напряже­ния и тока на входе двухполюсника; — ц> = - — аргумент ком­плексной проводимости. Из (2.67) следует, что любой пассивный двухполюсник можно представить схемой замещения, состоящей из параллельного соединения элементов с активной проводимостьюG и реактивной проводимостью В. Элемент с активной проводимос­тью — это всегда резистивный элемент с проводимостью G, а эле­мент с реактивной проводимостью — это индуктивный элемент с ин­дуктивной проводимостьюB_L=1 /ыЬ = Д если В > 0, или емкост­ный элемент с емкостной проводимостью В_с = из С = \ В |, если В < 0.

В зависимости от знака реактивной проводимости В комплексная проводимость пассивного двухполюсника имеет индуктивный (В > 0 для рис. 2.35, а) или емкостный (В< 0 для рис. 2.35, б) характер.

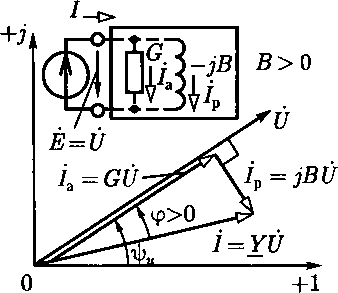
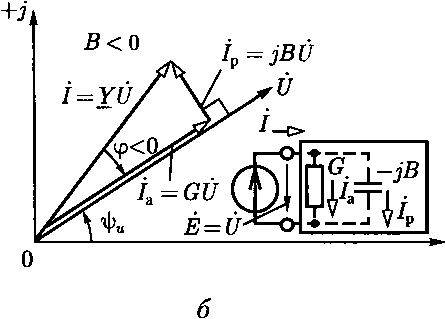
Умножив проводимости всех сторон треугольника проводимос- тей (рис. 2.35) на комплексное значение напряжения U = UZi\>_и, по­строим векторную диаграмму токов (рис. 2.37) для эквивалентной схемы замещения пассивного двухполюсника, где /_а =GUи /_р = —jBU — активная и реактивная составляющие тока /. Векто­ры комплексных значений /_а, /_р и / образуют на комплексной плос­кости треугольник токов:

/ = /. + /р. (2.68)

Модуль вектора активной составляющей тока /_а = /coscp, при­чем активная составляющая тока совпадает по фазе с напряжением. Модуль вектора реактивной составляющей тока /_р=/|sin<p|; вектор /_р образует с вектором напряженияUугол |тг/2|. Индуктивный реак­тивный ток отстает по фазе от напряжения на угол тт/2 (рис. 2.37, а). Емкостный реактивный ток опережает по фазе напряжение на угол тт/2 (рис. 2.37, б).

 

Из треугольников токов следует, что

Учитывая соотношения (2.67) и (2.68), получим различные ма­тематические выражения комплексной мощности пассивного двух­полюсника (2.60):

S = P + jQ =С/7* =U(i*+ /*) =Y*U²=GU²+ jBU².(2.69)

2.17. Эквивалентное преобразование схем последовательного соединения элементов в параллельное

В схемах замещения цепей синусоидального тока иногда необхо­димо преобразовать последовательное соединение элементов в эк­вивалентное параллельное, чтобы упростить анализ некоторых элек­тротехнических устройств, например катушки индуктивности с маг- нитопроводом (см. гл. 8).

Предположим, что задано последовательное соединение резис­тивного элемента с сопротивлениемRи элемента с реактивным со­противлением X (рис. 2.38, а). Комплексное сопротивление и про­водимость соединения соответственно равны

Z= R + jX;

^х=1⁼ пТ]х ⁼я²+х^{2 =} R² + x²~^jR² + x^2=a~^{jR (2J0)}

Параллельное соединение элементов (рис. 2.38, б) будет эквива­лентно последовательному (рис. 2.38, а), если комплексные прово­димости или сопротивления обоих соединений одинаковые, т.е.

⁼ -^jBss-^jwfx*'^(271б)

^эк

I—JX_ F

Ш

и

а                    б Рис. 2.38

Из (2.71) следует, что сопротивле­ния элементов, соединенных парал­лельно, выражаются следующим об­разом через сопротивления элемен­тов, соединенных последовательно:

Дзк =             *эк =                              (2.72)

Выразив из (2.72) сопротивления элементов, соединенных пос­ледовательно, получим условия обратного эквивалентного преоб­разования.

2.18. Электрическая цепь со смешанным соединением элементов

Последовательность расчета общего сопротивления смешанного соединения в цепях синусоидального тока такая же, как и в цепях по­стоянного тока (см. 1.9): сначала рассчитывается эквивалентное со­противление ветвей, соединенных параллельно, а затем после замены параллельных ветвей элементов с эквивалентным сопротивлением — сопротивление полученного последовательного соединения.

—1—2

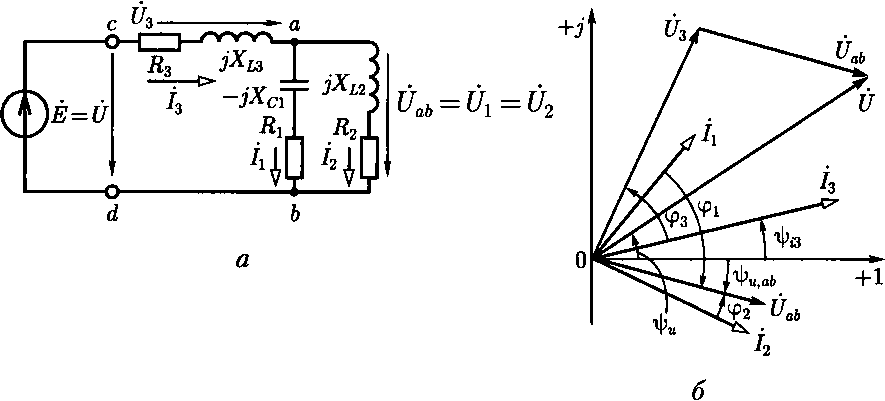
В качестве примера рассмотрим цепь на рис. 2.39, а. Определим сначала эквивалентное комплексное сопротивление двух параллель­ных ветвей, включенных между узлами а и Ь:

Z — Я A- iX — Zр^эк₌

— ¹¹ЭК I Jf-Л. _эк — п_ж с —

где

z, = r_x-jx_cl=v*^[4]; = Щ + jX_L2= Z₂e*>

— комплексные сопротивления параллельных ветвей. Общее сопро­тивление цепи между выводами с иd

z=z<₆+ z_3k,

где

= R₃+ jX_L3=Z₃e* з. Комплексные значения тока / и напряжений на участках i-V =________________________ ^U-_________ =Le^-

³ZДз + Л_эк + Х^₃+Х_эк) ³ и_з = Z₃i₃= Z₃e**I₃e*>« = u₃e^;

U,=U₂ = U_ab= Zj₃= г_же^1₃е*'« = U_abe^.

Применив закон Ома, найдем комплексные значения в каждой параллельной ветви:

U и U _Le^j^^ab., • U . U

Г -     ₌    ___ ₌ Г _еЛ 1. Т               ₌^UabC____ _ т

Рис. 2.39

 

На рис. 2.39, б приведена векторная диаграмма токов и напряже­ний анализируемой цепи.

Комплексная мощность источника ЭДС равна сумме комплекс­ных мощностей всех пассивных ветвей:

S= uiз*= s_x + s₂ + s₂ = irj* + u₂i* + uJi =

= Р_г + P₂+ P₃+ j(Q_cl+ Q_L2+ Q_L3) = = RJl + ЪЦ + R₃Ii + j(~X_clIf + + X_L3I₃).

2.19. Баланс мощности в цепи синусоидального тока

В любой момент времени алгебраическая сумма мгновенных мощностей всех источников энергии равна алгебраической сумме мгновенных мощностей всех приемников энергии. То же самое можно сказать и относительно средних значений мощностей за период.

Рассмотрим сначала приемники энергии, схемы замещения ко­торых содержат резистивные, индуктивные и емкостные элементы. Энергетические процессы в резистивных, индуктивных и емкостных элементах различны по физической природе. В резистивных элемен­тах происходит необратимое преобразование электрической энер­гии в другие виды энергии. Средняя скорость необратимого процес­са преобразования энергии в резистивном элементе определяется активной мощностью P_R[см. (2.50)]. В индуктивных и емкостных элементах происходит периодическое аккумулирование энергии в магнитных и электрических полях, а затем энергия возвращается во внешнюю относительно этих элементов часть цепи. В таких элемен­
тах нет необратимого преобразования электрической энергии в дру­гие виды, т.е. активная мощность Рравна нулю. Электрические про­цессы в индуктивном и емкостном элементах определяются реак­тивной индуктивной мощностьюQ_l[см. (2.52)] и реактивной емко­стной мощностьюQ_c[см. (2.54)].

Баланс мощности в электрической цепи синусоидального тока, содержащей произвольное число источников энергии, т. е. источни­ков тока и источников ЭДС (напряжения), и приемников энергии, т. е. резистивных, индуктивных и емкостных элементов, означает, что, во-первых, алгебраическая сумма активных мощностей всех источ­ников энергии равна арифметической сумме мощностей всех резис­тивных элементов:

Е ^hct^HCTCOS^ - =Yj^RIR

Или

1>ист=£^ря-                                     (2.73)

во-вторых, алгебраическая сумма реактивных мощностей всех ис­точников энергии равна алгебраической сумме реактивных мощно­стей всех индуктивных и всех емкостных элементов:

Е и_ист1_исгм^и - гм = Еад² -

или

£«о                        (2.74)

Слагаемое алгебраической суммы активных или реактивных мощ­ностей источника ЭДС (рис. 2.40, а) записывается со знаком плюс, если положительное направление тока / совпадает с направлением действия ЭДС Ё = U_ab.В противном случае (рис. 2.40, б) слагаемое записывается со знаком минус (например, генератор синусоидаль­ной ЭДС, работающий в режиме двигателя). Аналогично для источ­ника токаJ = i(рис. 2.40, в) слагаемое записывается со знаком плюс и в противном случае (рис. 2.40, г) — со знаком минус.

Баланс мощности в электрических цепях синусоидального тока можно выразить в комплексной форме: алгебраическая сумма ком-

-Оа

-Оа

-О а Uab о ь

-О а Uab

E=Uab

E=Uab

©

©

-Об

-об

-ob

jxA . -jxc

о—nzt

E2=U2 о

ь

Ri

О

Рис. 2.41

плексных мощностей всех источников энергии равна алгебраичес­кой сумме комплексных мощностей всех приемников энергии:

Знаки слагаемых алгебраической суммы комплексных мощнос­тей источников энергии выбираются по тому же правилу, что и для их активных и реактивных мощностей.

Для приемников энергии слагаемые записываются со знаком плюс (минус), если положительные направления напряженияU_UOT и тока /_пот совпадают (противоположны).

В общем случае в качестве приемников энергии можно рассмат­ривать не отдельные элементы, а ветви цепей или двухполюсники.

В качестве примера составим баланс мощности цепи на рис. 2.41:

=Ej* - Ej* - Uj* = £Р_ИСТ +

---

Дата добавления: 2018-02-28; просмотров: 485; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!