КАТУШКА С МАГНИТОПРОВОДОМ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 7 страница

2.9. Первый и второй законы Кирхгофа в комплексной форме

Математическая формулировка законов Кирхгофа для цепей си­нусоидального тока зависит от выбранного способа представления синусоидальных величин.

Первый закон Кирхгофа. По первому закону Кирхгофа алгеб­раическая сумма токов в любом узле электрической цепи в каждый момент времени равна нулю:

= 0,                                (2.37)

k=1

т. е.

п

8т(ш« + г|)_Л) = 0,

к=1

где п — число ветвей, сходящихся в узле. В дальнейшем все синусо­идальные токи, положительные направления которых выбраны к узлу (от узла), будем записывать со знаком минус (плюс).

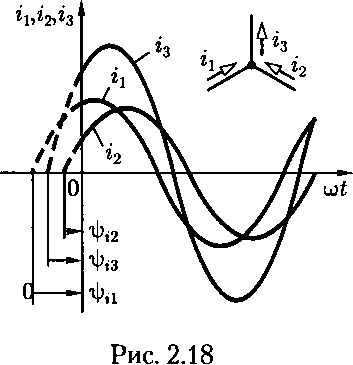
На рис. 2.18 в качестве примера для одного из узлов построены мгновенные значения трех синусоидальных токов

h = Imi^sinM+ "Фill h=^Jm2 sin(wt + иi₃= /_ш3sin(utf + г|)_<3) при выбранных положительных направлениях. По первому закону Кирхгофа

з

ХЛ=-h-h+h=О к=1

для любого момента времени.

Чтобы получить математическую формулировку первого закона Кирхгофа в комплексной форме, представим все синусоидальные токи в (2.37) соответствующими им комплексными значениями (2.21):

h = h^ik-

Первый закон Кирхгофа в комплексной форме записывается сле­дующим образом:

ЕЛ=0,                                  (2-38)

к=1

т. е. алгебраическая сумма комплексных значений токов всех ветвей, сходящихся в каком-либо узле цепи синусоидального тока, равна нулю. Здесь комплексные значения токов, для которых положитель­ные направления выбраны к узлу (от узла), записываются со зна­ком минус (плюс).

На рис. 2.19 построена векторная диаграмма трех токов:

ii = Ii^n, h= /2^2»h = h^iz- На векторной диаграмме должно выполняться равенство

£Д = -/₁-Д + /₃ = о.

к=1

 

Второй закон Кирхгофа. По второму закону Кирхгофа алгебра­ическая сумма напряжений всех участков любого контура в каждый момент времени равна нулю:

т

£«* = 0,                                  (2.39)

к=1

т.е.

т

YjUmk sin(urt Н-г^) = О,

А:=1

где напряжения, положительные направления которых совпадают (противоположны) с выбранным направлением обхода контура, за­писываются со знаком плюс (минус); т — число участков. В частно­сти, для контура схемы замещения, содержащего только пассивные элементы (резистивные, индуктивные, емкостные) и источники ЭДС, в каждый момент времени алгебраическая сумма напряжений на пассивных элементах контура равна алгебраической сумме ЭДС:

п      тп

ХЧ=£^е*                                  (2.40)

к=1 к=1

или

п                              т

Y^^Umk sin(wt + ita ) = 5~2^ЕшкSin М + *Ф ек )>

к=1 к=1

где пит — соответственно числа пассивных элементов и ЭДС в контуре. В выражении (2.40) напряжения и_к и ЭДС е_к9 для которых положительные направления совпадают (противоположны) с про­извольно выбранным направлением обхода контура, записываются

Например, для выбранного на схе­ме замещения (рис. 2.20) контура 1 по

(2.39)

щ — щ — щ + щ = о>

для контура 2 по (2.40)

u_L= е_х -

Второй закон Кирхгофа в комплек­сной форме получим, представив все синусоидальные величины в (2.39) и

со знаком плюс (минус). щ

и2 Рис. 2.20

(2.40) соответствующими комплекс­ными значениями по (2.21):

 

Рис. 2.21

U_k = U_kZ^_uknE_k =E_kZ^_ek,

т.е.

m

£4 = 0                                    (2.41a)

k=1

и

n      m

J2U_k = E^_k-                               (2-416)

k=1 fc=l

В уравнениях (2.41) со знаком плюс (минус) записываются ком­плексные значения напряжений и ЭДС, положительные направле­ния которых совпадают (противоположны) с произвольно выбран­ным направлением обхода контура.

Например, для выбранного на схеме цепи (рис. 2.21, а) контура 1 по (2.41а)

и_г - и₂ - и₃ + и_А = о,

для контура 2 по (2.416)

и_к-и_ь = Ё₁-Ё₂.

Те же контуры 1и2 показаны на схеме замещения с синусоидаль­ными величинами (рис. 2.20).

На рис. 2.21, б построена векторная диаграмма ЭДС и напряже­ний контура 2, которая наглядно иллюстрирует второй закон Кирх­гофа в комплексной форме.

2.10. Комплексный метод расчета цепей синусоидального тока

Между мгновенными значениями синусоидальных величин (2.20) и их комплексными значениями (2.21) существует взаимно одно­значное соответствие. Поэтому для описания режима работы цепи синусоидального тока можно применять любой из этих способов представления синусоидальных величин. Однако в случае представ­ления синусоидальных величин комплексными значениями запись законов Ома и Кирхгофа упрощается ввиду отсутствия тригономет­рических функций.

Совместное решение алгебраических уравнений, составленных на основе законов Ома и Кирхгофа, для определения комплексных зна­чений токов и напряжений всех элементов цепи, т. е. применение ком­плексного метода расчета, — достаточно простая задача. По найден-

Таблица 2.3 Представление синусоидальных ЭДС и токов источников комплексными значениями Источник Мгновенное значение Комплексное значение Условное изображение ЭДС Тока е = £msin(urt + г[>е) J{t) = /msinM + Ь) Е V2 j = I™ езЬ V2 «ф *ф Л» ф .'ф

 

 

Таблица 2.4 Комплексные сопротивления и проводимости пассивных элементов Элемент Параметр Комплексное сопротивление Комплексная проводимость Резистивный R R 5-" Индуктивный L juL = jXL зз—л Емкостный С   juC = jBc

ным комплексным значениям можно записать при необходимости и соответствующие им мгновенные значения синусоидальных ве­личин.

При расчете режима работы цепи синусоидального тока комплек­сным методом полезно выделить несколько логически самостоятель­ных этапов:

1) представить исходные данные о параметрах всех элементов цепи в комплексной форме. Это означает, что, во-первых, синусои­дальные ЭДС источников напряжения или токи источников тока, заданные мгновенными значениями (в тригонометрической форме), следует представить комплексными значениями (табл. 2.3) и, во- вторых, для индуктивных и емкостных элементов цепи нужно опре­делить соответствующие комплексные сопротивления или комплек­сные проводимости (табл. 2.4);

2) выбрать положительные направления для токов во всех вет­вях, указав их стрелками на схеме замещения;

3) пользуясь законами Ома и Кирхгофа в комплексной форме и учитывая выбранные положительные направления токов в вет­вях, составить систему уравнений, определяющую режим работы цепи;

4) решить полученную систему уравнений, т.е. определить комп­лексные значения токов в ветвях цепи и комплексные значения на­пряжений на ее элементах.

Найденные комплексные значения токов и напряжений однознач­но определяют соответствующие им мгновенные значения синусо­идальных токов и напряжений.

В качестве примера рассмотрим расчет комплексным методом цепи синусоидального тока со схемой замещения на рис. 2.22, содер­жащей В 5 ветвей, из которыхBj = 1 ветвь имеет источник тока J(t)= J_wsin(u)£ + г|;./), и У = 3 узла, а также источник ЭДС е = E_msin(ut + 'Фе).

б

Для этого выполним последовательно все этапы расчета.

1. Представим синусоидальные ЭДСe(t)и токJ(t)источников со­ответствующими комплексными значениями [см. (2.21) и табл. 2.3]:

Определим комплексные сопротивления индуктивногоjwL=jX_L и емкостного1/juC=—jX_cэлементов (см. табл. 2.4).

На рис. 2.22, б изображена схема, для которой исходные данные о параметрах всех элементов представлены в комплексной форме.

2. Выберем положительные направления неизвестных токов в вет­вях (рис. 2.22, а) и совпадающие с ними положительные направления напряжений на пассивных элементах. Положительные направления соответствующих им комплексных значений такие же (рис. 2.22, б).

3. При выбранных положительных направлениях токов и напря­жений составим У—1 = 3 — 1 = 2 независимых уравнения по перво­му закону Кирхгофа для узлов а и к

-J - i_e+ i_L= 0; - i_L- i_c+ i_R= 0                          (2.42a)

иК = В — Bj—У + 1 = 5 — 1 — 3 + 1 = 2 независимых уравнения по второму закону Кирхгофа для контуров 1 и 2 (без источников тока!):

U_L-U_C=E; U_R-U_C= 0,

или

jX_Li_L+jx_ci_c= Ё\                              (2.426)

Ri_R- jx_ci_c= О,                               (2.42b)

где учтены соотношения (2.29), (2.32), (2.36) законов Ома в комп­лексной форме:

U_R=Ri_R;U_L = jXj_L\ Uс = jx_ci_c.

4. Решив совместно систему четырех алгебраических уравнений (2.42), определим комплексные значения токов:

I_R= /_де*Чi_L=                   i_c= /_се^Лс;I= J_ee*4

Для найденных значений токов запишем соответствующие им мгновенные значения:

i_R=yf2I_R sin (иЛ + г|>ю);i_L=V2I_L sin (иЛ + г^);

г_с — V2 I_c sin+ г|)_<С7);i_e= \Г21_еsin(ut+ a|;_ie).

Комплексные значения напряжения определяются по закону Ома, а мгновенные значения записываются аналогично мгновенным зна­чениям токов.

Для расчета системы уравнений (2.42) с помощью ЭВМ ее следу­ет представить аналогично (1.13) в матричной форме подобно (1.10):

1	0	0	0	0	ij		l	0	0	0	0	j
0	1	-1	0	0	ie		-l	0	0	0	0	Ё
0	0	1	1	-1	h	—	0	0	0	0	0	0
0	0		jXc	0	ic		0	1	0	0	0	0
0	0	0	-jXc	R	iR		0	0	0	0	0	0

 

где ток в ветви с источником токаIj — J.

Для линейных цепей синусоидального тока, так же как и для ли­нейных цепей постоянного тока, справедлив принцип наложения (см. 1.12). Поэтому для упрощения анализа линейных цепей синусои­дального тока можно применять различные методы расчета, кото­рые были рассмотрены при анализе линейных цепей постоянного тока: метод преобразования схем (см. 1.9), метод узловых потенциа­лов (см. 1.10), метод контурных токов (см. 1.11), метод эквивалент­ного источника (см. 1.14) и др. При этом математические формули­ровки различных методов расчета цепей постоянного тока остаются справедливыми и для расчета цепей синусоидального тока. Нужно только все ЭДС, напряжения и токи заменить комплексными зна­чениями соответствующих синусоидальных величин, а сопротивле­ния элементов — комплексными сопротивлениями.

В дальнейшем для понятий комплексные значения ЭДС, напря­жения, токи и т. д, а также соответствующих им векторов комплек­сных значений будем пользоваться и сокращенными терминами, например комплексный ток или просто ток.

2.11. Неразветвленная цепь синусоидального тока

В неразветвленной цепи (рис. 2.23) при действии источника си­нусоидальной ЭДС е =E_msin(wt+ я|;_е) ток также синусоидален: г = I_msm(ut+ г^) и напряжения на резистивном, индуктивном и ем­костном элементах

% = U_Rmsm(ut + -фид);u_L= U_Lmsm(ut+ и_с = {7_Cwsin(utf +

Для расчета режима работы неразветвленной цепи комплексным методом представим все синусоидальные величины соответствую­щими комплексными по (2.21):

E = EZ^_e] i = /Zi|v>

На рис. 2.23 стрелками изображе­ны положительные направления тока, ЭДС и напряжений.

Uc

Выберем направление обхода кон­тура и запишем уравнение по второ­му закону Кирхгофа (2.41):

U_L + U_R + U_C =

= jwLi + Ri- j/uCi = Ё; (2.43)

здесь учтен закон Ома для резистивного (2.29), индуктивного (2.32) и емкостного (2.36) элементов.

Из (2.43) найдем комплексный ток в цепи:

I =

; Ё

R + XqjL-I/QJC)'

или

U

(2.44)

R + j(uL-l/uCy

гдеU — Ue^j^^u= Ё = Ee^j^^e— напряжение между выводами источ­ника и пассивного участка.

Величина, стоящая в знаменателе выражения для комплексного тока (2.44), называется комплексным сопротивлением (неразветвлен- ного участка цепи):

Z—R + j[uL -l/(uC)]= R + j(X_L- X_c). (2.45a)

Величина, обратная комплексному сопротивлению, называется комплексной проводимостью:

Рис. 2.23

У= 1 /Z.

xL>x0	' jx i
-jXc
Я

+з

+1

+з

JXL

+1 -jXc

ф<0Rб

Каждому значению комплексного сопротивления Z, т. е. комплек­сному числу, соответствует точка на комплексной плоскости. Ее по­ложение однозначно определяется вектором на комплексной плос­кости (рис. 2.24). Этот вектор является геометрической интерпрета­цией комплексного сопротивления и имеет такое же обозначение Z Слагаемые комплексного сопротивления изображены на рис. 2.24 также в виде векторов для двух случаев:X_L> Х_с (рис. 2.24, а) и X_L< Х_с (рис. 2.24, б). Геометрическая интерпретация комплексно­го сопротивления позволяет легко перейти от алгебраической фор­мы записи комплексного сопротивления (2.45а) к тригонометричес­кой и показательной формам:

Z = Zcosip + jZ sincp;                      (2.456)

Z= Ze* = Z Z ф,                            (2.45b)

гдеZ — \Z\ = yjR^[3]+ (X_L— X_c)²— модуль комплексного сопротив-

_x (X_L- Х_с)

ления или полное сопротивление; Ф = arctg---------------- — аргумент

К

комплексного сопротивления. В зависимости от знака величины (X_L— Х_с) аргумент комплексного сопротивления может быть либо положительным (ф > 0 — индуктивный характер комплексного со­противления, как на рис. 2.24, а), либо отрицательным (ф < 0 — ем­костный характер комплексного сопротивления, как на рис. 2.24, б), но всегда |ф| < -к/2.

Подставим значение комплексного сопротивления в показатель­ной форме (2.45в) в (2.44). При этом ток в цепи будет определен по закону Ома для неразветвленной цепи:

• Е _ Е Z~ Z

или

+1

+1

Рис. 2.25

о

о

б

а

Если комплексное сопротивление цепи имеет индуктивный ха­рактер, то токiотстает по фазе от напряженияU,так как ф > О (рис. 2.24, а) и по (2.47) < Если комплексное сопротивление цепи имеет емкостный характер, то ток в цепи опережает по фазе напря­жение, так как ф < О (рис. 2.24, б) и по (2.47) г^ >a|j_tt.На векторной диаграмме положительное значение угла ф отсчитывается против направления движения часовой стрелки от вектора комплексного значения тока /, а отрицательное значение — по направлению дви­жения часовой стрелки.

---

Дата добавления: 2018-02-28; просмотров: 446; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!