КАТУШКА С МАГНИТОПРОВОДОМ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 3 страница

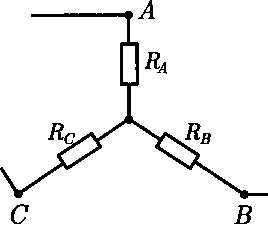
Проводимость между узлами А и В для схемы треугольника на рис. 1.15, а

Rab+Rbc+Rca

Rab Rbc+ Rca RabRbc+ RcaRab

Сопротивление между узлами А и В — величина, обратная про­водимости между этими узлами, т. е.

Кав^ВС +RCARAB Rab +Rbc +Rca

Для схемы звезды на рис. 1.15, б сопротивление между теми же узлами А и В равно сумме сопротивлений двух ветвей:R_A+ Rb-

Согласно условию эквивалентности должно выполняться равен­ство

bca

о , о _RabRBC+RCARAB_ RABRBC+RCARAB. /л 17ч

Rab +Rbc +R(

здесь ^2Ra~ сумма сопротивлений всех ветвей для треугольника.

1

Структуры треугольника и звезды по отношению к узлам сим­метричны. Поэтому уравнения равенства сопротивлений между уз­лами В и Си между узлами Си А можно получить из (1.17) простой циклической перестановкой индексов:

RbcRca +RabRbc.

IX

RcaRAB+RBCRCA

(1.18)

Rb+Rc —

(1.19)

Rc +ra ~

Чтобы определить сопротивлениеRAзвезды, сложим (1.17) и (1.19) и вычтем из этой суммы (1.18); разделив полученное на 2, най­дем

XX

(1.21) (1.22)

(1.20)

и _RabRCA Сопротивления других ветвей звезды получим путем цикличес­кой перестановки индексов:

р _ RbcRab. и _ RqaRbC

В случае равенства сопротивлений ветвей треугольника (R_AB= = R_BC= R_ca= R_a)сопротивления ветвей эквивалентной звезды тоже одинаковы:

R_r=Дд/3.                                  (1.23)

Возможно обратное преобразование звезды из резистивных эле­ментов в эквивалентный треугольник.

Для этого перемножим попарно выражения (1.20) — (1.22) и сло­жим полученные произведения:

R_aR_b+R_BR_C+ R_cRA = и u^D°^R1^AU •

^пав "г ^пвс "г п_са

Последнее уравнение разделим на (1.22) и определим сопротив­ление ветви треугольника:

RaRB Rc

(1.24)

^rab - ^ra+ ^rb +

Путем циклической перестановки индексов в (1.24) найдем вы­ражения для сопротивлений двух других ветвей:

RbRC. RA

(1.25)

Rbc —Rb +Rc+

RriR

^rca - ^rc + ^ra + г>

Примером упрощения расчетов может служить преобразование мостовой схемы соединения резистивных элементов (рис. 1.16, а). После замены одного из треугольников эквивалентной звездой всю цепь (рис. 1.16, б) можно рассматривать как смешанное соединение резистивных элементов.

1.10. Метод узловых потенциалов

Метод узловых потенциалов позволяет уменьшить число совме­стно решаемых уравнений до У — 1, где У— число узлов схемы заме­щения цепи. Метод основан на применении первого закона Кирхго­фа и заключается в следующем:

1) один узел схемы цепи принимаем базисным с нулевым потен­циалом. Такое допущение не изменяет значения токов в ветвях, так как ток в каждой ветви зависит только от разностей потенциалов узлов, а не от действительных значений потенциалов;

2) для остальных У — 1 узлов составляем уравнения по первому закону Кирхгофа, выражая токи ветвей через потенциалы узлов;

(1.26)

3) решением составленной системы уравнений определяем по­тенциалы У — 1 узлов относительно базисного, а затем токи ветвей по обобщенному закону Ома (1.8).

Рассмотрим применение метода на примере расчета цепи по рис. 1.17, содержащей У = 3 узла. Узел 3 принимаем базисным, т. е. = 0. Для узлов 1 и 2 уравнения по первому закону Кирхгофа:

узел 1

h + h + Ji = о;

узел 2

h-h- h=0,

где

Л = (ч>1 - Фз)/#1 = 4>i/Ri>

Д3'

k = (ф2 ~ Фз)/#2 = Ф2/Й2; h= (ф 1 - Ф2 +E)/R₃,

т.е. после подстановки

(1.27а)

Рис. 1.18

Рис. 1.17

или в матричной форме

J_ ₊ J_ _J_

R\#2 Дз

1 0 0 1

Ф1 Ф2

-Jl

R:3 E_ R3

(1.276)

Jo

R, R>2 RS

Решение системы уравнений (1.27a) методом подстановок или (1.276) численным методом на ЭВМ определяет потенциалы узлов Ф! и ф₂>^а следовательно, и токи ветвей по (1.8).

Из (1.27) очевиден принцип составлений уравнений по методу уз­ловых потенциалов. В левой части уравнений коэффициент при по­тенциале рассматриваемого узла положителен и равен сумме прово- димостей сходящихся к нему ветвей. Коэффициенты при потенциа­лах узлов, соединенных ветвями с рассматриваемым узлом, отрица­тельны и равны проводимостям соответствующих ветвей.

Правая часть уравнений содержит алгебраическую сумму токов ветвей с источниками токов и токов короткого замыкания ветвей с источниками ЭДС, сходящихся к рассматриваемому узлу, причем слагаемые берутся со знаком плюс (минус), если ток источника тока и ЭДС направлены к рассматриваемому узлу (от узла).

EE/R

(1.28)

и12 =Ч>1~Ч>2 =

U

Выражение (1.28) называется формулой межузлового напряже­ния. Например, для цепи на схеме рис. 1.18 напряжение между узла­ми по (1.28) ^ EJR, +EJR, + E3/R3 1/^ + 1/^+1/^ '

В частном случае схемы замещения без источников тока с двумя узлами потенциал узла 1 при базисном узле 2, т. е. при ф₂ = 0> равен напряжению между узлами:

1.11. Метод контурных токов

Метод контурных токов позволяет уменьшить число совместно решаемых уравнений до К = В — Bj —У+1и основан на примене­нии второго закона Кирхгофа.

Рассмотрим сущность метода сначала для расчета схемы цепи без источников тока, т.е. при В₃ = 0:

1) выбираем К = В - У+ 1 независимых контуров и положитель­ных направлений так называемых контурных токов, каждый из ко­торых протекает по всем элементам соответствующего контура.

Для планарных схем, т. е. допускающих изображение на плоско­сти без пересечения ветвей, достаточным условием выделения К не­зависимых контуров является наличие в каждом из них хотя бы од­ной ветви, принадлежащей только этому контуру;

2) для К независимых контуров составляем уравнения по второ­му закону Кирхгофа, совместное решение которых определяет все контурные токи;

3) ток каждой ветви определяем по первому закону Кирхгофа как алгебраическую сумму контурных токов в соответствующей ветви.

В качестве примера рассмотрим расчет цепи на рис. 1.19, а с чис­лом ветвей В = 6, узлов У = 4, независимых контуров К = В — У +1 = = 6 — 4 + 1 = 3. Выберем независимые контуры 1-3 и положитель­ные направления контурных токов в них /_и, /₂₂ и /₃₃ (рис. 1.19, б). В отличие от токов ветвей каждый контурный ток обозначим двойным индексом номера контура. Уравнения по второму закону Кирхгофа:

контур 1

(+ #4 +)hi ~ ^6^22 +R4I33 — - Е_а; контур 2

+ ( ^2 + + #6 )^22 + Я5/33 = \ контур 3

iJ₄J_n+ ii₅/₂₂+ ( Д₃ + J?4 + #5 )/₃3= E₃—J?4,

(1.29а)

или в матричной форме

*4 R3+ i?4+ i?5

11 22

+ #4 +Rq

А

1зз

-R₆Щ + Щ + R₆

R_л

1	0	0
0	1	0
0	0	1	E3

(1.296)

 

б

Решение системы уравнений (1.29а) методом подстановок или (1.196) численными методами на ЭВМ определяет контурные токи 1_п, /₂₂, /₃₃. Токи ветвей (рис. 1.19) находим по первому закону Кирх­гофа: = /_и, /₂ = /₂₂, /₃ = /₃₃, /₄ = — 1ц — /₃₃, /₅ = /₂₂ + /₃₃, Iq = 1\1 — /₂₂.

Из (1.29) очевиден принцип составления уравнений по методу контурных токов. В левой части уравнений коэффициент при кон­турном токе рассматриваемого контура положителен и равен сумме сопротивлений его ветвей. Коэффициенты при контурных токах в контурах, имеющих общие ветви с рассматриваемым контуром, рав­ны сумме сопротивлений общих ветвей со знаком плюс (минус), если направления контурных токов в общих ветвях совпадают (противо­положны).

Правая часть уравнений содержит алгебраическую сумму ЭДС ветвей рассматриваемого контура, причем слагаемое записывается со знаком плюс (минус), если направления ЭДС и положительное направление контурного тока совпадают (противоположны).

При расчете схемы замещения с ис­точниками тока возможны упрощения. Контурный ток, выбранный так, что дру­гих контурных токов в ветви с источни­ком тока нет, известен. Поэтому в схеме с В ветвями, В jиз которых содержат ис­точники тока, число независимых конту­ров без источников тока и соответству­ющих им неизвестных контурных токов равноK = B-Bj-У-f1.

Рис. 1.19

Например, в цепи на схеме рис. 1.20 число ветвей В = 5, ветвей с источниками токаBj—2, узлов У = 3, независимых кон­туров без источников тока К = В — В₃ — -У + 1=5 — 2 — 3 + 1 = 1 (контур 3).

Уравнение по второму закону Кирхгофа для контура 3 при выбран­ных положительных направлениях контурных токов:

R\h\ —R2I22 + (#1 + + Я₃)/₃₃ = Е,

т.е.

j₌Е - flj/n + Д₂/₂₂

где I_n= J_b/₂₂ = J₂— известные токи контуров У и 2. Токи ветвей: Л = /_и + /₃₃; /₂ = /₃₃ - /₂₂; /₃ = /₃₃.

1.12. Принцип и метод наложения (суперпозиции)

Для линейных электрических цепей справедлив принцип нало­жения: ток в любой ветви равен алгебраической сумме токов в этой ветви (частичных токов) при действии каждого источника в отдель­ности, если остальные источники заменяются резисторами с сопро­тивлениями, равными внутренним сопротивлениям соответствую­щих источников[2].

На основе принципа наложения для расчетов линейных цепей применяется метод наложения (суперпозиции).

В схеме замещения с В ветвями ток каждой к-й ветви равен ал­гебраической сумме частичных токов от действия каждой из ЭДС ветви г и каждого источника тока Jj ветвиj.

Для схемы без источников тока метод наложения определяется системой (1.12):

h ⁼G_kiE_x+ ад + ... + G_kkE_k+ ... + G_klE_i -f... + G_kBE_B, (1.30)

гдеG_kk= l[^Ek)/E_k— собственная проводимость ветви к, равная от­ношению частичного тока ветви к ЭДС источника этой ветви при ус­ловии, что ЭДС остальных источников равны нулю;G_H= I_k^Ei>/ Е_г — взаимная проводимость ветвей А; и г, равная отношению частичного тока ветви к к ЭДС источника ветви г при условии, что ЭДС осталь­ных источников равны нулю.

Собственная проводимость ветви имеет положительное значение, так как по договоренности (см. 1.8) положительное направление ее тока и ЭДС источника выбираются одинаковыми. Взаимная прово­димость двух ветвей может иметь положительное и отрицательное значения (1.13), причем

G_kt=G^                                 (1.31)

что означает выполнение принципа взаимности.

М)

(ег)

Рис. 1.21

М)

ЛЬ)

И

Взаимная проводимость отрицательная, если при выбранном по­ложительном направлении частичного тока в ветви к его численное значение получается отрицательным (действительное направление частичного тока противоположно положительному).

Принцип взаимности выполняется для всех линейных цепей с независимыми источниками. Но он в общем случае не справедлив для линейной цепи с зависимыми источниками, например для схе­мы замещения усилителя в режиме малого сигнала.

В качестве примера рассмотрим расчет методом наложения цепи на рис. 1.21, я. Токи ветвей равны сумме частичных токов в схемах на рис. 1.21, бив:

Л = ГГ + 'Г²⁾ = ад + G₁₂E₂=                               - ||Е₂;

1₂ = + /<*> = + G₂₂E₂= + h = I^{₃^Ei)+ /f²⁾=G₃₁E, + G₃₂E₂ =§E₁₊ ||-E₂,

где собственные проводимости ветвейG_nи G₂₂имеют положитель­ные значения, взаимные проводимости ветвейG_u= G₂1 — отрица­тельные значения, a G_S1и 6?₃₂ — положительные значения (1.14) и обозначеноR = *JR_XR₂+RyR^ + #2^3-

В схемах замещения с источниками тока частичные токи ветвей определяются от каждого из них при исключении остальных источ­ников тока в результате разрыва содержащих их ветвей.

1.13. Принцип компенсации

Различают принципы компенсации напряжения и компенсации тока. Принцип компенсации напряжения заключается в том, что уча­сток а-Ь схемы с напряжениемU_abможно заменить эквивалентным

-0-V

E= U_ab,

u₂

. U2

 

Рис. 1.22

источником ЭДСE=U_ab,направление действия которого противо­положно положительному направлению напряженияU_ab.Доказа­тельство принципа следует из второго закона Кирхгофа (1.6), в ко­тором любое слагаемое суммы напряжений участков можно перене­сти с противоположным знаком в правую часть уравнения, что эк­вивалентно замене соответствующего участка источником ЭДС. Например, уравнения контуров цепи на рис. 1.22, а

---

Дата добавления: 2018-02-28; просмотров: 350; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!