Оптимизация модулей и фаз узловых напряжений при наличии ИРМ в нагрузочных узлах.
В данном случае оптимизация режима сети проводится по критерию минимизации потерь активной мощности при передаче энергии, в качестве оптимизируемых параметров при этом рассматриваются модули и фазы узловых напряжений, мощности ИРМ и коэффициенты трансформации.
Оптимизация узловых напряжений, соответствующих минимуму потерь активной мощности возможна благодаря включению в нагрузочных узлах компенсирующих устройств – источники реактивной мощности, обеспечивающих баланс при заданном напряжении. При этом целевая функция – суммарная потеря активной мощности в энергосистеме.
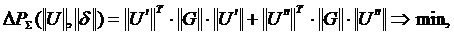
где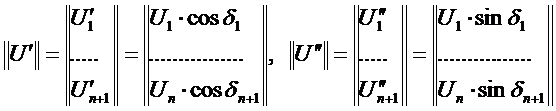 
-вектора-столбцы мнимых и действительных узловых напряжений.
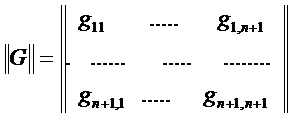-матрица собственных и взаимных узловых проводимостей, n-число независимых узлов.
Под номером n+1 в уравнения входит узел, являющийся балансирующим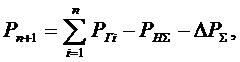 
и базисным 
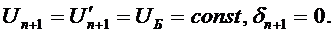Таким узлом может быть узел, через который происходит экспорт/импорт энергии из другой энергосистемы того же либо более высокого иерархического уровня, или шины низшего напряжения подстанции, являющиеся центром питания распределительной сети. В данном примере в качестве независимых переменных Х могут быть выбраны модули напряжений независимых узлов, а в качестве зависимых Y-фазные углы. При применении метода приведенного градиента первый итерационный шаг включает в себя следующие пункты:
1. Задаются начальные приближения независимых параметров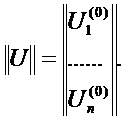 
|
|
|
2. Определяются значения зависимых переменных, удовлетворяющих совместно с U(0) уравнениям установившего режима (условию баланса активной мощности в узлах)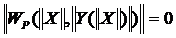 
, например, в итерационном цикле по методу Ньютона, в котором повторяется операция 
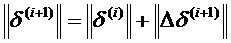пока 
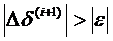, где 
-вектор столбец величин, характеризующих точность расчёта, 
, 
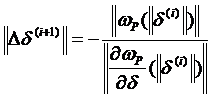- вектор-столбец небалансов активной мощности, состоящий из n элементов, i-й элемент которого 
, Рi = РГi – РНi – разность генераторной и нагрузочной мощностей в i-м узле.
3. В точке 
определяется приведенный градиент целевой функции по независимым переменным 
, где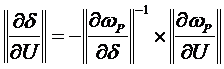 
.
4. Итерационные шаги 
повторяются, пока 
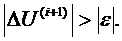На каждом i-м шаге повторяется пункт 2 – определение 
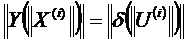- исходя из условия 
. Мощность источников реактивной мощности определяется из условия баланса реактивной мощности в узлах при подстановке найденных оптимальных значений 
зависимых и независимых параметров. Условие баланса для i-го узла
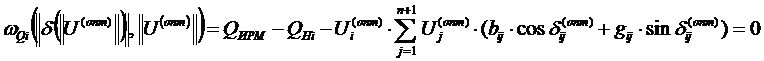откуда мощность ИРМ в данном узле
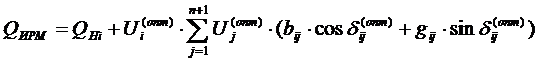
Оптимизация коэффициента трансформации в ЦП РС
В качестве независимого параметра Х принимаются U в ЦП Un+1 зависящий от КТ в качестве зависимых параметров: модули и фазы U остальных узлов РС.
|
|
|
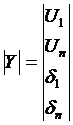Задаётся начальное приближение U в ЦП U0 n+1 и определяется значение зависимых параметров Y из условия баланса 
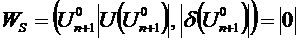* т.к. в узле нет ИРМ, а число независимых переменных 2n то в системе * входят балансы P Q для каждого узла. Далее находим распределение по методу Ньютона:
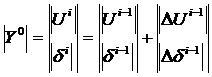и повторяется пока не будет выполняться условие сходимости.
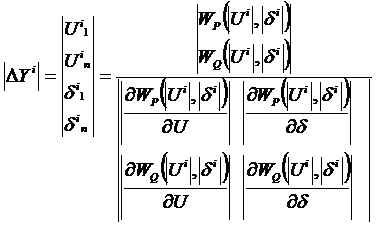
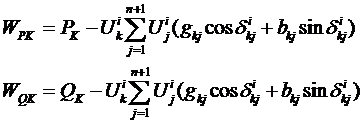
В точке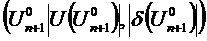 
определяется приведённый градиент целевой функции по независимому параметру Un+1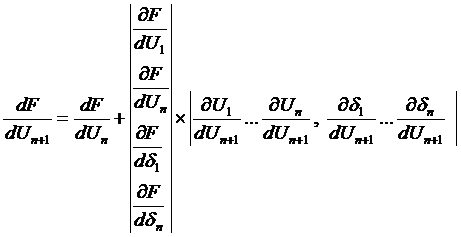 
Итерации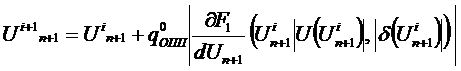 
выполняются до тех пор, пока не будет выполняться условие сходимости.
Дата добавления: 2018-02-15; просмотров: 987; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!