Методы возможных направлений.

Методы относятся к классу итеративных методов, в которых строится последовательность точек 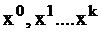, стремящихся к абсолютному экстремуму целевой функции  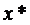на основании критерия оптимизации, т.е. 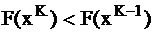, 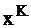лучше, чем .

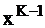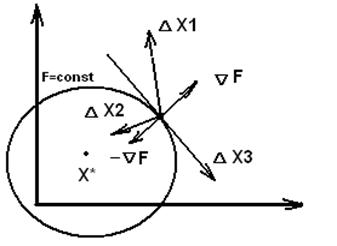Суть методов возможных направлений заключается в том, что спуск от начального приближения  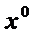до абсолютного экстремума  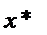может осуществляться различными направлениями, называемыми возможными.

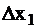- рост целевой функции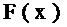

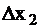- уменьшение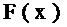

-

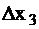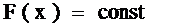
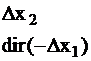 - возможные направления

Вектор, ортогональный к касательной функции, указывающий направление роста целевой функции называется градиентом целевой функции.

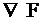-градиент целевой функции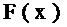

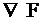- - антиградиент является наилучшим из возможных направлений, указывающий путь наискорейшего убывания целевой функции.

Способы задания длины шага

,

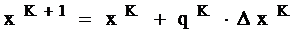где 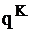- длина шага вдоль вектора ;

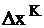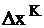- направление спуска на К-ом шаге.

  Все методы нелинейного программирования, основанные на данном соотношении можно разделить на 2 класса по способу задания длины шага:

1) Класс основан на постоянной длине шага

       Исходная длина шага задается примерно. Но при неудачно заданной длине шага может не выполняться критерий оптимизации, т.е.

 

 

нарушение критерия оптимизации, отсюда следует

,

,

.

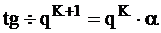Достоинством этих методов является малый объем вычислений на каждом шаге.

Недостатки – при неудачно заданных значениях длины шага q и 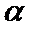, возможно большое количество шагов оптимизации, и следовательно, большой объем вычислений.

2) Класс - метод наискорейшего спуска

длина шага зависит от направления спуска 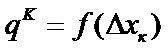 и вычисляется из условия наискорейшего убывания целевой функции

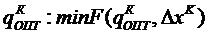
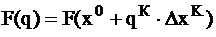
Для того, чтобы найти оптимальное значение длины шага 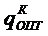необходимо продифференцировать по длине шага и приравнять к нулю:

:

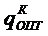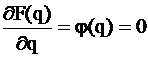
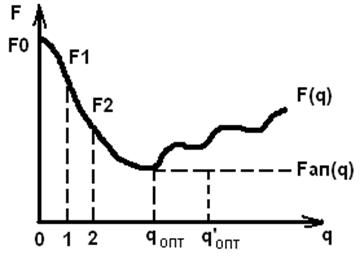
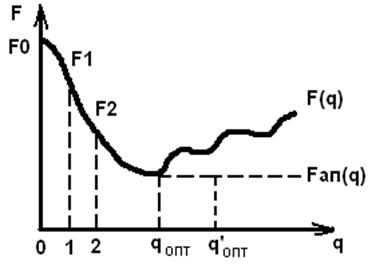
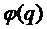 - данная функция может быть нелинейной относительно q, и поэтому  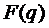аппроксимируют полиномом 2-ой степени

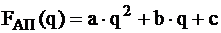
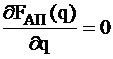псевдооптимальная длина шага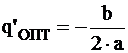

 

Найти

?         

 

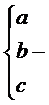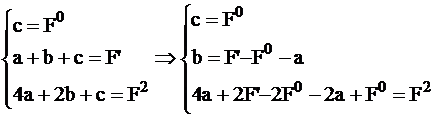
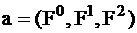
26. Применение метода наискорейшего спуска при решении задач оптимизации в электроэнергетике.

 

Метод наискорейшего спуска

Длина шага зависит от направления спуска  и вычисляется из условия наискорейшего убывания целевой функции

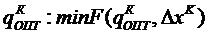
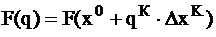
Для того, чтобы найти оптимальное значение длины шага 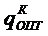необходимо продифференцировать по длине шага и приравнять к нулю:

:

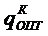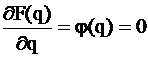
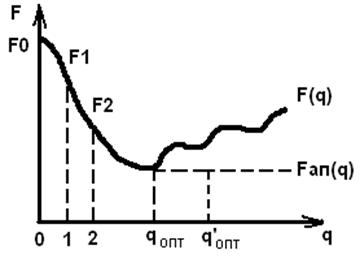
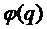 - данная функция может быть нелинейной относительно q, и поэтому  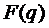аппроксимируют полиномом 2-ой степени

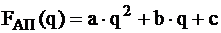
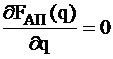псевдооптимальная длина шага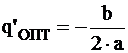

 

Найти

?   

 

 

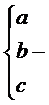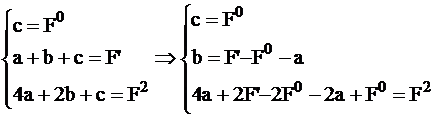
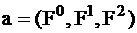
27.Способ вычисления оптимальной длины шага вдоль заданного направления спуска при решении задач оптимизации в электроэнергетике.

,

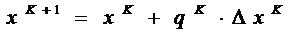где 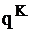- длина шага вдоль вектора ;

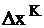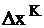- направление спуска на К-ом шаге.

  Все методы нелинейного программирования, основанные на данном соотношении можно разделить на 2 класса по способу задания длины шага:

3) Класс основан на постоянной длине шага

       Исходная длина шага задается примерно. Но при неудачно заданной длине шага может не выполняться критерий оптимизации, т.е.

нарушение критерия оптимизации, отсюда следует

,

,

.

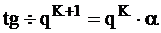Достоинством этих методов является малый объем вычислений на каждом шаге.

Недостатки – при неудачно заданных значениях длины шага q и 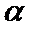, возможно большое количество шагов оптимизации, и следовательно, большой объем вычислений.

4) Класс - метод наискорейшего спуска

Длина шага зависит от направления спуска 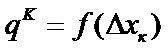 и вычисляется из условия наискорейшего убывания целевой функции

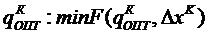
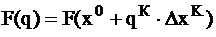
Для того, чтобы найти оптимальное значение длины шага 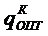необходимо продифференцировать по длине шага и приравнять к нулю:

:

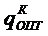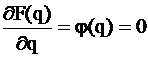
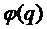 - данная функция может быть нелинейной относительно q, и поэтому  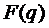аппроксимируют полиномом 2-ой степени

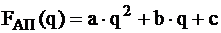
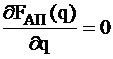псевдооптимальная длина шага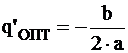

 

 

Найти

?     

 

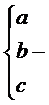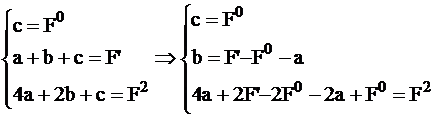
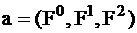
28-29Применение метода покоординатной оптимизации в электроэнергетике. Внешний и внутренний циклы метода.

 

Метод покоординатной оптимизации относится к регулярным методам выбора направления. Суть алгоритма в том, что в кач-ве возможных направлений исп-ся орты исходной схемы координат.

                               

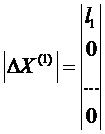
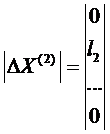
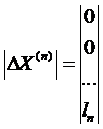
        Внутренний цикл

1ый шаг: изменение Х₁

                            Х₂ =соnst 

                               . . .

                            Х_n =соnst 

Х₁⁽¹⁾= Х₁⁽⁰⁾+q₁оптl₁      

Х₂⁽¹⁾= Х₂⁽⁰⁾+q₂оптl₂          

 . . .

Х_n⁽¹⁾= Х_n⁽⁰⁾+q_nоптl_n             

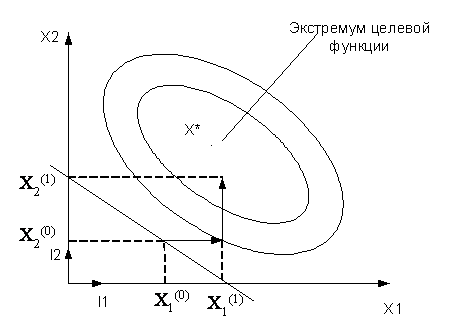Частичная минимизация по всем N независимым переменным образуют полный внешний цикл. Кол-во повторений внутреннего цикла заранее не известно и определяется св-вами целевой функции и начальным приближением.

 

определение q¹опт

ΔХ₁⁽¹⁾= Х₁⁽¹⁾-Х₁⁽⁰⁾= q₁опт*l₁      

ΔХ₂⁽¹⁾= Х₂⁽¹⁾-Х₂⁽⁰⁾= q₂опт*l₂

Достоинства:простота реализации и малый объем вычислений на каждом шаге.

Недостатки:возможная неудовлетворительная сходимостьинеприемлемое число шагов.

 

---

Дата добавления: 2018-02-15; просмотров: 1451; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!