Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике.
Понятие оптимизации. Основные задачи оптимизации в электроэнергетике. Степени свободы электроэнергетической системы. Допустимый и оптимальный режимы.
птимальным режимом работы - режим в соответствии с некоторым критерием оптимальности.
Оптимизация – задача решение которой выявляется оптимальный режим.
Критерий оптимальности:
- количественный (снижение расхода условного топлива на ТЭС);
- качественный (улучшение влияния электроэнергетического объекта на экологию).
Задачи оптимизации в электроэнергетике:
1. Стратегия развития энергосистемы;
2. Выбор оптимальной конфигурации эл.сетей, соединяющих подсистемы или распределяющих передающих энергию внутри сети;
3. Оптимальное распределение нагрузки между электростанциями;
4. Оптимальная стратегия использования материальных ресурсов;
5. Выбор оптимальных маршрутов грузоперевозки, в т.ч. перевозки топлива;
6.Выбор точек размыкания линии с двухсторонним питанием;
7. Выбор маршрута осмотра электротехнических объектов.
Взаимосвязь расчета установившегося режима и его оптимизации.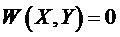 
Параметры уравнения установившегося режима 
:
- 
- независимые, заданные параметры;
- 
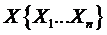- зависимые параметры.
Уравнения установившегося режима связывают между собой его параметры.
Пусть k – число уравнений, n – число неизвестных. Если k=n, то система полностью определена. При k<n система недоопределена. Избыток числа неизвестных над числом уравнений физически означает что система имеет (n-k) степеней свободы.
|
|
|
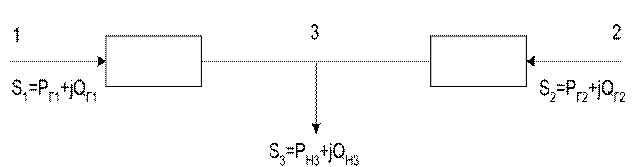
УУР БМ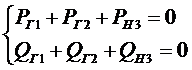 
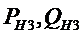- заданы
Система имеет 2 степени свободы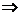 
2 любых параметра могут быть заданы в пределах минимальных и максимальных допустимых значений.
Регулируются P и Q:
- с помощью регулирующих трансформаторов;
- при включении/отключении оборудования.
Из всех возможных состояний системы наибольший интерес представляют допустимые режимы, в которых значения параметров установившегося режима находятся в заданных пределах.
Задача оптимизации: найти наиболее экономичный режим.
Рост числа степеней свободы – рост возможности оптимизации и усложнение задач.
| генератор | нагрузка | ||
| Z | X | Q, 
| U,
|
| Y | P,U | P,Q |
В задаче оптимизации используются добавочные степени свободы для изменения переменных параметров режима, чтобы из множества состояний системы выбрать такое, которое обеспечит минимальный суммарный расход условного топлива, что снижает экономические затраты.
При оптимизации режима за счет наличия степеней свободы выбираются параметры режима, обеспечивающие минимальные суммарные потери активной мощности.
Применение метода множителей Лагранжа при решении задач оптимизации в электроэнергетике.
|
|
|
Дата добавления: 2018-02-15; просмотров: 1385; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!