Применение градиентных методов оптимизации в электроэнергетике. Критерии сходимости. Градиентный метод в сочетании с методом наискорейшего спуска.

В отличие от методов покоординатной оптимизации градиентные методы не связаны с набором фиксированных направлений, а движение всегда осуществляется в направлении наискорейшего убывания целевой функции.

Выбор градиента определяется через производные по всем независимым переменным

▼

Рекуррентное выражение градиентного метода

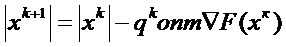
Для организации скорейшего спуска определяем удовлетворяющую условию q_опт

q^к_опт: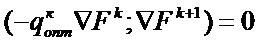

вектор спуска  таков, что новый градиент ортогонален предыдущему Х⁽⁰⁾.

Плюсы и минусы:         

Программное обеспечение градиентных методов значительно сложнее, а объем вычислений значительно больше, чем при использовании метода покоординатной оптимизации. Однако, в сочетании методом наискорейшего спуска сходимость градиентных методов значительно лучше.

 

 

Критерии сходимости

1) сопоставление целевой функции на каждом шаге

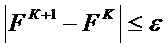
ε – малая величина

если это условие выполняется то экстремум достигнет максимума.

Достоинствапростота реализации.

Недостатки: малость модуля разности целевой функции на соседних шагах может не соответствовать близости к экстремуму.

2) Проверка длины градиента

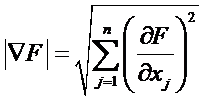
в точке экстремума все

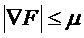, µ - малая величина.

Тогда процесс точно сойдется.

Спуск выполняется до .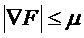

Метод проецирования градиента.

Пусть необходимо найти минимум выпуклой функции, при условии что независимые переменные удовлетворяют системе линейных ограничений в форме неравенств.

F(x)àmin

В начале точки х⁰ фазовые координаты удовлетворяют условиям |А||х|<|B| определяется вектор градиент dF/dx и в обратном ему направлении производится движение за границу допустимой области х¹.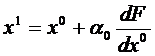

 - некий множитель определяющий величину шага за границу допустимой области.

       Получается точка х¹, которая проецируется на поверхность |А||х|<|B| в результате чего определяется точка 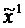. Из этой точки, так же как и из х⁰ в направлении антиградиента совершается направление за границу допустимой области в точку х².  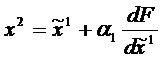. х² проецируется на поверхность ограничений и тем самым определяется  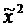и так далее.

 

35-36Учет ограничений в форме равенств при решении задач оптимизации в электроэнергетике. Приведенный градиент

При решении задач оптимизации должны учитываться уравнения связи, задающие зависимость между переменными Х и У. Число зависимых переменных – М ограничено числом уравнений связи. Ограничения в форме равенств:

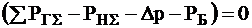 (БАМ) или

M: Y₁…Y_m через N X₁…X_n;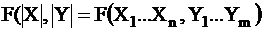

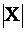 и 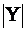 векторы зависимых и независимых переменных.

; Рассмотрим т-у ;

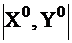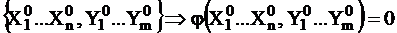
Разложив в ряд Тейлора: 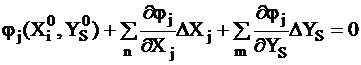; в матричной: |∆X||∂φ/∂X|+ |∆Y||∂φ/∂Y| = 0     переходя к бесконечномалым приращениям:

 - матрицы частных производных уравнения связи зависимых и независимых переменных. С учетом зависимости: |Y(|X|)| ц.ф. можно представить в виде F=(|X|, |Y|X||) только с независимыми переменными.

Выражение градиента приобретает вид:

(*)

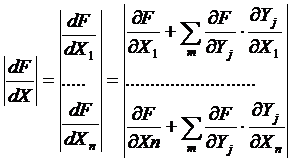
,где 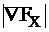 и 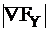 вектор-столбцы частных производных ц.ф. по Х и Y

 подставим в (*)

Вектор полных производных целевой функции по независимым переменным называется приведенный градиент→метод приведенного градиента

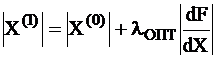 - I шаг. Другой метод, учитывающий ограничения в форме равенств, это метод Лагранжа:  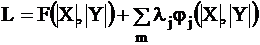- функция Лагранжа. , В(Р)-расход топлива на ТЭС

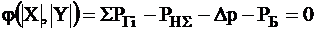 - Функция ограничения в виде равенств.

 

---

Дата добавления: 2018-02-15; просмотров: 1481; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!