Определение оптимального распределения нагрузки между ТЭС методом множителей Лагранжа. Относительный прирост топлива.
Метод позволяет отыскать условные или относительные экстремумы функции, которые являются ее минимумом или максимумом при выполнении дополнительных условий в форме равенств, т.е. уравнений связи.
Данный метод дает возможность найти систему уравнений, которой удовлетворял экстремум функции 
на множестве N. Для того чтобы найти экстремум, характеризующийся на множестве N вектором 
необходимо найти m чисел 
, которые совместно с вектором 
удовлетворяют 
уравнениям с 
неизвестными.
Эти уравнения получены как условный экстремум функции Лагранжа.
Например, найти Р.
Заданы расходные характеристики
- целевая функция
Уравнения ограничения 
Уравнения связи – расходные характеристики
Функция Лагранжа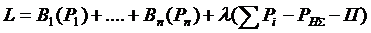 
Условие оптимальности распределения нагрузки: 
Наивыгоднейшее распределение нагрузки между ТЭС без учета потерь активной мощности. Физический смысл равенства относительных приростов.
Это случай задачи наивыгоднейшего распределения нагрузки между агрегатами электростанций или в ЭС с высокой концентрацией мощности.
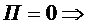
-усл-ие оптимальности, т.е. оно соотв-ет рав-ву отн-ых приростов
Рассмотрим на примере из 2-х агрегатов Эл/ст
Условие оптимальности – затраты топлива на единицу мощности в месте её потребление равны на Эл. Станциях. На практике bi не удовлетворяют этому условию и подлежат корректировке по методике.
Определение оптимального распределение нагрузки в энергосистеме с ГЭС и ТЭС методом множителей Лагранжа. Относительные приросты ТЭС и ГЭС.
З-ча наив-шего распределения нагр-и в гидротепл. Системе делится на:
1 З-ча оптим-ции длит-ных реж-ов; 2 З-ча оптим-ции краткосрочн. режим (сутки и менее).
Для всего цикла регул- ия ГЭС находит наив-шее распр-е нагрузки м/у всеми станциями сист-ы, и опр-ет оптим режим исп-ния гидроресурсов, т.е. график сработки и заполнения водохранилищадля всей ГЭС с-мы. На основании этих расчётов регламентируются гидроресурсы на более короткий период оптим-ции.
Метод множителей Лагранжа
1 Ур-ние цели 
- расход топлива эквив-ой ТЭС за период времени Т 
2 Ур-ние связи
2.1 
- расх-ая хар-ка ТЭС
2.2 
- расх хар-ка ГЭС
3 Ур-ние огр-ний
-ур-ний: 
- сумма нагр-ки, 
- сумма потерь.
ур-ние: 
- заданные огр-ния по стоку для j-ой ГЭС, 
- расход, с которым работала ГЭС в период Т
- мощн-ти 
-ой ГЭС на инт t
4 Ф-ция Лагранжа
Кол-во неиз-ых 
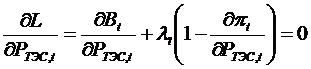
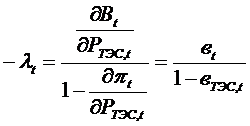
ур-ний: 
; …. 
, где 
, 
ур-ний: 
(*)
Все величины, вход-щие в сист-у ур-ний (*) опр-ся энерг-ми хар-ми оборуд-ния, т.е. отн-ный прирост расх топлива (В) и расх топлива на ТЭС (q), или же парам-ми сети.
Индексы при этих велич-ах можно опус-ть
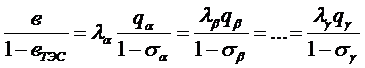
- усл оптим-ции режима гидро-теплов с-мы.
Смысл усл-ия оптим-ции
В том, что для наив-шего распр-ия нагрузки необх-мо в теч всего периода оптим-ции собл-ть пост-ное соотн-ние 
м/у ТЭС и каж-ой из ГЭС, т.е. м/у ТЭС и 
-ГЭС нагрузка должна рапр-ся по соотн-ию
и это постоянное соотн-ие должно собл-ся в теч. всех периодов оптим-ции
Соотн-ие м/у ТЭС и 
-ГЭС
При усл-вии соблюдения баланса величины 
, 
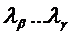связывают м/у собой режимы ТЭС и соотв-щей ГЭС.
Дата добавления: 2018-02-15; просмотров: 1924; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!