Оптимизация режима энергосистемы с учетом потери активной мощности при передаче.
Один из методов, применяемы для определения потерь активной мощности при передаче электроэнергии, является линейный метод коэффициентов токораспределения.
Суть заключается в следующем: ток каждой ветви в рассматриваемом режиме может быть получен как сумма токов частных режимов.
Присутствуют только в 1 из независимых узлов. Таким образом число таких частных режимов равно n – числу независимых узлов.
Например схема замещения на рис. 3.9 а содержит 6 узлов 6 ветвей. Необходимо пронумеровать ветви и узлы, 1 из них выбрать в качестве балансирующего. Далее следует произвольно задать условно положительные направления ветвей.
Частный режим токораспре-деления представлен на рис 3.9.в.
В данном случае схему замещения можно представить так
Далее расчет ведем методом линейных коэффициентов токораспределения.
Для данной схемы справедливы ур-я:
для тока 5-ой ветви 
Если предположить что сопротиления всех линий равны то для тока 3 –ей ветви
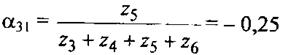
Знак ”-” возникает поскольку направление тока противоположно условно-положительным направлениям. Аналогичным образом вычисляются а41 а61.
Как следует из рисунка ток в ветви 2 отсутствует т.е. а21=0 следовательно а11=0.
Коэффициенты токораспределения вычисляются аналогичным образом для частных режимов и могут быть представлены в виде матрицы коэффициентов:
В соответветствии с методом наложения ток каждой из ветвей определяется как сумма токов, протекающая по этой ветви во всех частных схемах
|
|
|
При равенстве всех узловых напряжений 
для n+1, где n+1 – число узлов, комплексная мощность протекающая по i-ой линии: 
Тогда потери при передаче мощности по i-ой линии: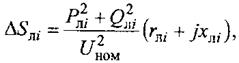 
В том числе акт. составляющая потерь:
И суммарные по энергосистеме потери: 
Знание зависимости суммарных потерь позволяет определить относительные приросты суммарных потерь передаваемой мощности. при изменении мощности какой либо электростанции.
Условие оптимального распределения активной мощности между электростанциями с учетом потерь.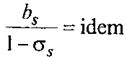 
Формулировка задачи оптимизации режима энергосистемы с позиций нелинейного программирования.
Основные определения: линия поверхности равного уровня целевой функции, допустимая и результирующая области, абсолютный и условный экстремум целевой
Основные определенияОбщая задача отыскание экстремума целевой функции задании ограничения в виде равенств и неравенств, является задачей нелинейного программирования. Выражение целевой функции через зависимые и независимые переменные. Целевую функцию можно рассматривать как функции независимых X и зависимых Y переменных F=ФИ ||X||,||Y||), где Х=(x1…xn) и Y=(y1…yn) - вектора, соответственно независимых и зависимых переменных, n - число независимых переменных, т - число зависимых переменных. Если целевой функции является суммарный расход топливной энергосистеме, то в качестве независимых переменных может рассматриваться активные и реактивные мощности генераторных узлов ||X|| - PГ i , QГ I где i=1…n - номер электростанции, а в качестве зависимых переменных ||Y|| - напряжение генераторных UH1…Um нагрузочных UГ1…Un узлов и мощность балансирующего узла P. Таким образом, оптимальное значение целевой функции: BOРТ = minB(||X||,||Y||) с учетом связи между и зависимыми и независимыми переменными ФИ(||X||,||Y||). Уравнения связи.В качестве уравнений связи можем использовать уравнения узловых напяжений, записанные в форме баланса токов для каждого узла
|
|
|
Si*/Ui* - YiБUБ – 
YijUj = 0 где i=1…n, n – число независимых узлов или же в матричном виде. ||S*\||U*||-||YБ|| UБ = ||Y||x||U||
Мощность уравнений связи целевую функцию можно выразить через независимые переменные F=F(Х). Длялюбых векторов РГ, QГ можно найти узловые токи ||I||, из узловых уравнений в форме баланса токов Ii=Si*\Ui* - YБiUБ напряжения U=||Y||-1||I|| мощность балансирующего узла 
целевая функция представляется как функция только с независимыми переменных F=F(||Х||) частности для оптимизации режима электростанций B=B1||P1||+B2||P2||+…Bn||Pn|| + BБ||PБ(||P||)||, где Bi||Pi|| - расходные характеристики электростанций. Оптимальный режим должен удовлетворять режимным йниям, в общем случае в виде системы неравенств , xi MIN <xi<xiMAX, i=1…n; yjMIN <xj<xjMAX, j=1…m; zS MIN <zS(||X||,||Y||)< zS MAX, s=1…S
|
|
|
S - некий контролируемый параметр, являющийся функцией от векторов зависимых и независимых переменных, которые не входят в целевую функцию. Например, если вектор независимых параметров – мощности электростанций независимых узлов и зависимый параметр - мощность балансирующего узла входят в целевую функцию, то в качестве вектора. Z могут быть выбраны узловые напряжения, которые (если пренебречь потерями активной мощности при передаче электроэнергии) не оказывают влияния] суммарный расход топлива в энергосистеме (на целевую функцию но зависят от оптимизируемых параметров. Расчет узловых напряжений позволило в каждом итерационном шаге контролировать допустимые оптимизируемого режима, Линия поверхности равного уровня целевой функции Линия (поверхность) равного уровня целевой функции геометрическое место точек в пространстве независимых переменных, в которых целевая функция имеет одно и тоже значение F=(X)=const. На рис. линии равного уровня целевой функции отчечены как замкнутые кривые, образующие элленпсы вокруг которой соответствует экстремум целевой функции. Допустимая и результирующая области DХ - допустимая область по параметрам X, поскольку для области выполняется система неравенств x1 MIN <x1<x1MAX и x2 MIN <x2<x2MAX. В общем случае, при наличии n независимых переменых область n - мерный параллелограмм, в данном случае для визуальной наглядности число независимых переменных выбрано равным. На допустимую область DХ накладываются границы допустимых областей DY и DZ. Здесь X - вектор оптимизируемых параметров, в координатах, которых ищется экстремум целевой функциям, Y, Z – контролируемые параметры, которые зависят от параметров оптимизируемые ограничения на которые могут нарушаться в процессе оптимизации. Границы допустимых областей для Y, Z в коор, оптимизируемых параметров - это геометрическое место (значений оптимизируемых параметров), которым соответствуют граничные значения контролируемых параметров. Область D - выпуклая, если для любой пары точек, прямая, соединяющая эти две точки, также целиком принадлежат области D. Абсолютный и условный экстремум целевой функции Абсолютный экстремум X* - точка в координатах независимых переменных, которой соответствует предельное значение целевой функции. Условный или относительный экстремум X'* - это то границе области D, в которой целевая функция имеет предельное, значение внутри данной области. Значения независимых параметров в точке X’*соответствующее им значение целевой функции F=(X’*) решение задачи оптимизации.Целевая функция может быть мультимодальной и унимодальной. В первом случае найденное решение может быть локальным, во втором случае оно всегда глобально. Активные и пассивные ограниченияОграничения параметров могут быть активные придающие параметрам в точке условного экстремума граничное значение, как, например, параметрам Z или же пассивные.
|
|
|
21-25Применение методов возможных направлений для поиска экстремума целевой функции при решении задач оптимизации в электроэнергетике. Возможные направления. Градиент и антиградиент целевой функции. Способы задания длинны шага. Метод оптимизации при постоянной длине шага.
Дата добавления: 2018-02-15; просмотров: 1767; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!