Размерность и физический смысл множителей Лагранжа в задачах оптимизации распределения нагрузки в энергосистеме.
Размерность и физический смысл множителей Лагранжа
1 ТЭС и 1 ГЭС
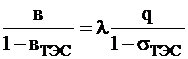если пренебречь потерями 
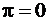, то усл-вие оптим-ции
; 
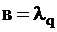
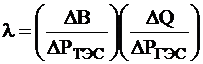
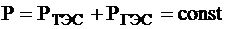
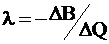
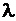- мера эффект-ти использ-я гидроресурсов, т.е. ккая экономия топлива будет получена на ТЭС при измен-ии расхода на ГЭС на 
.
Наивыгодн-ший режим тот, при к-ом эфф-сть исп-ния ресурсов на к-ой ГЭС одинакова на всём периде оптим-ции, т.е.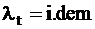 
; 
; 
; 
, 
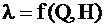
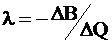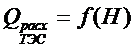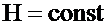
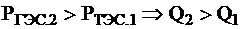
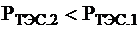
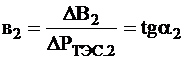
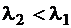
Эффект-ть использ-я гидроресурсов в данной с-ме (т.е. в с-ме с недозагруженной ГЭС) пропорц-на расходу на ГЭС.
Если ГЭС работает с малым расходом, то в с-ме имеется неэкон-но работающая ТЭС.
Оптимальное распределение нагрузки при постоянном напоре ГЭС и структурная схема алгоритма поиска данного распределения.
Для наивыгоднейшего распределения нагрузки необходимо по методу Лагранжа в процессе расчёта подобрать l в соответствии с заданным стоком ГЭС и найти такое распределение нагрузки, при котором lt = const для всего периода оптимизации
Дано:
1) Р1, Р2 ..РК t1 …tК – нагрузки
2) Расходные характеристики В(РТЭС ), Q(PТЭС )
3) Характеристики относительных приростов q(PГЭС ), b(PТЭС)
4) Ограничение по стоку и по мощностям станций W задано ГЭС
РТЭС max; РТЭС min; РГЭС max; РГЭС min.
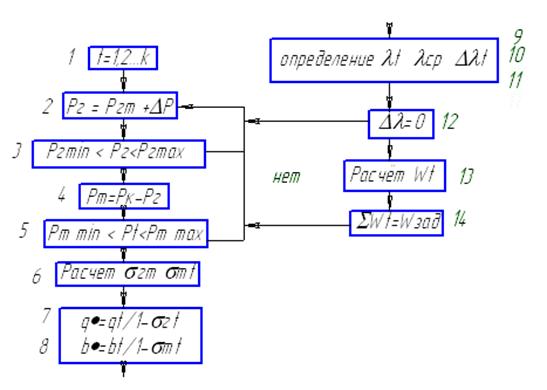
2- Задаются мощности ГЭС для каждого интервала, и проверяется его допустимость -3. Если условия не выполняется мощность, корректируется мощностью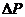 
-4 определяем мощность ТЭС из условия баланса мощностей проверяем ограничения – 5. Определяем суммарное прирост потерь для каждой Эл ст и определяем суммарные приросты для всех интервалов 7,8
|
|
|
Определяем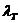 
для каждого интервала – 9 среднее и отклонение. В зависимости от знака 12 корректируются мощности (2).
14.Оптимальное распределение нагрузки при переменном напоре ГЭС.
Изменение напора приводит к колебаниям уровней верхнего и нижнего бьефов.
ЭЭС: 1ТЭС и 1ГЭС → произвольное распределение графика нагрузки
; 
; 
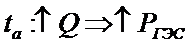
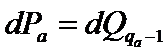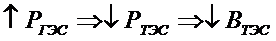
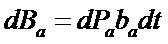- экономия топлива на ТЭС;
;
; 
; 
; 
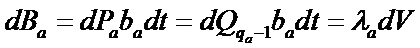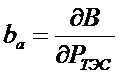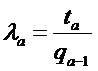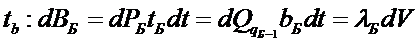- дополнительный расход топлива из-за ↓Q.
; 
;
; 
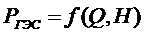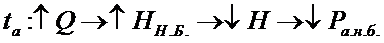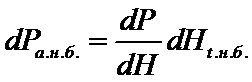
ta : дополнительный расход топлива, вызванный повышением уровня нижнего бьефа.
;
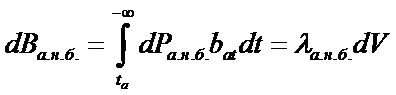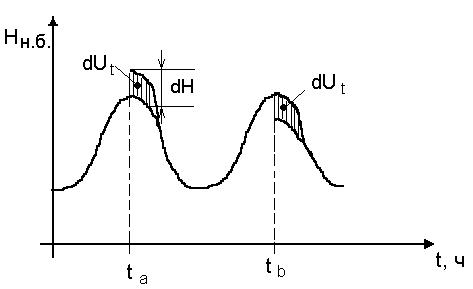
В момент tБ : 
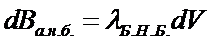
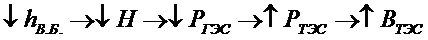
изменение мощности из-за изменения 
; 
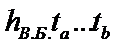
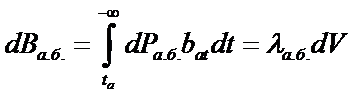Общее изменение расхода топлива:
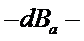экономия топлива из-за ↑Q в tA;
дополнительный расход топлива из-за ↓Q в tБ;
дополнительный расход топлива из-за ↑ 
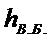в tA;
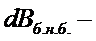экономия топлива из-за ↓ 
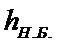в tБ;
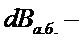дополнительный расход топлива из-за ↓ 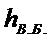в tA… tБ;
Если режим I лучше режима II → 
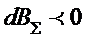→ режим II экономичнее режима I
- условие равноэкономичности режимов
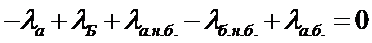
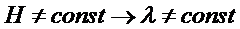
Оптимальное распределение нагрузки между агрегатами эл/ст.
Использование метода множителей Лагранжа позволяет получить условие наивыгоднейшего распределения нагрузки между агрегатами эл/ст. в виде равенств отношений приростов расхода первичного ресурса (приведенной мощности) к приращению вторичного ресурса (полезной мощности) при соблюдении балансовых ограничений. 1)М/у агрегатами ТЭС:
|
|
|
а) м/у турбинами: bT,i= ∆Di/∆Pi= idem
б) м/у котлами: bK,i= ∆Bi/∆Di= idem
в) м/у блоками: bБ,i= ∆Bi/∆Рi= idem
где ∆Di – прирост расхода пара; ∆Pi – прирост расхода мощности турбин; ∆Bi – прирост расхода топлива; bT,I – относительный прирост турбины; bk,I - относительный прирост котлов; bБ,I – относительный прирост блока (блок=котел+турбина)
На эти уравнения накладываются ограничения, т.к. характеристики имеют скачки и участки постоянного прироста.
bT1 bT2
min P1 max P min P2 max P
Р1>P2
Pmin1, Pmax1 – минимальная и максимальная мощность турбины 1
Pmin2, Pmax2 – минимальная и максимальная мощность турбины 2
Pmin=Pmin1+Pmin2
1. Если Pmin<P<Pmin+P2 – загрузка турбины 2
2. Pmin+P2<P<P1+P2 – загрузка агр.1
3. P1+P2<P<P1+Pmax2 – загрузка агр.2
4. P>P1+Pmax2 – загрузка агр.1
При такой методике всегда используется агрегат с наибольшей экономией топлива. Оптимальным является последовательность включения агрегатов ЭС в порядке возрастания их относительных приростов.
|
|
|
2) Распределение нагрузки м/у агрегатами ГЭС
Распределение нагрузки м/у агрегатами ГЭС является наивыгоднейшим, если они работают с одинаковыми относительными приростами.
Задача наивыгоднейшего распределения нагрузки м/у агрегатами станций проста, если известны характеристики относительных приростов. Но в условиях эксплуатации желательно использовать не характеристики, а измерение относительных приростов. Для этого с малым шагом дискретности измеряем а1 и а2 и соответствующие им Р1 и Р2.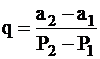 
Дата добавления: 2018-02-15; просмотров: 1265; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!