Вариант расчета 6. Метод Юлы.
Максимально плоская аппроксимация.
Расчет на максимум полосы
При заданном качестве согласования
В этом случае заданы средняя частота полосы согласования  ,
,  , параметры нагрузки и выходное сопротивление генератора. Расчет может быть проведен в следующей последовательности.
, параметры нагрузки и выходное сопротивление генератора. Расчет может быть проведен в следующей последовательности.
1. Достроим нагрузку до резонанса на средней частоте полосы согласования. Для этого определим резонансную частоту нагрузки  . Если
. Если  , то последовательно с нагрузкой следует включить дополнительную индуктивность
, то последовательно с нагрузкой следует включить дополнительную индуктивность  , где
, где  . Если же
. Если же  , то достройка нагрузки до резонанса на средней частоте
, то достройка нагрузки до резонанса на средней частоте  осуществляется последовательным включением дополнительной емкости
осуществляется последовательным включением дополнительной емкости  , где
, где  . Вначале проведем расчет низкочастотного эквивалента СЦ с последующим его преобразованием в полосовую согласующую цепь. При этом в качестве НЧ эквивалента нагрузки следует взять проследовательное соединение
. Вначале проведем расчет низкочастотного эквивалента СЦ с последующим его преобразованием в полосовую согласующую цепь. При этом в качестве НЧ эквивалента нагрузки следует взять проследовательное соединение 
 , если
, если  ,
, 
 , если
, если  и
и  . Емкость нагрузки будет восстановлена при преобразовании НЧ эквивалента СЦ в полосовую цепь.
. Емкость нагрузки будет восстановлена при преобразовании НЧ эквивалента СЦ в полосовую цепь.
2. Осуществим нормировку элементов  и
и  относительно
относительно  и неизвестной частоты среза (полосы согласования) низкочас-
и неизвестной частоты среза (полосы согласования) низкочас-
тотного эквивалента СЦ 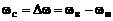 . В результате имеем
. В результате имеем 
 . Здесь значение
. Здесь значение  также неизвестно и подлежит определению в процессе расчета. Штрихами помечены нормированные элементы.
также неизвестно и подлежит определению в процессе расчета. Штрихами помечены нормированные элементы.
3. Определим оптимальные значения параметров аппроксимации  и
и  из условий физической реализуемости СЦ и максимальной полосы согласования при заданном значении
из условий физической реализуемости СЦ и максимальной полосы согласования при заданном значении  . Для этого определим нули передачи, их класс и кратность. Сопротивление нагрузки
. Для этого определим нули передачи, их класс и кратность. Сопротивление нагрузки  . Четная (параэрмитовая) часть сопротивления нагрузки (см. рис. 3)
. Четная (параэрмитовая) часть сопротивления нагрузки (см. рис. 3) 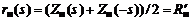 . Нулем передачи является нуль функции
. Нулем передачи является нуль функции  . Очевидно, что единственный нуль
. Очевидно, что единственный нуль  простой (не кратный, т.е.
простой (не кратный, т.е.  ). Поскольку
). Поскольку  , нуль передачи является нулем четвертого класса. Условиями физической реализуемости согласующей цепи являются [2, с. 69]
, нуль передачи является нулем четвертого класса. Условиями физической реализуемости согласующей цепи являются [2, с. 69]
|
|
|
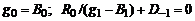 .
.
Здесь  и
и  – коэффициенты разложения в ряды Лорана функций
– коэффициенты разложения в ряды Лорана функций 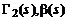 и
и  в нуле передачи.
в нуле передачи.
 задается в виде дробно-рациональной функции (для двухзвенной цепи отношением двух полиномов второй степени)
задается в виде дробно-рациональной функции (для двухзвенной цепи отношением двух полиномов второй степени)
 .
.
Коэффициенты  выражаются через параметры аппроксимации
выражаются через параметры аппроксимации
d и  при тейлоровской аппроксимации [2, с. 40]
при тейлоровской аппроксимации [2, с. 40]

Здесь  принимает значения
принимает значения 
 – коэффициенты стандарт-
– коэффициенты стандарт-
ных полиномов Баттерворта. Для  (двухзвенная СЦ)
(двухзвенная СЦ) 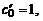
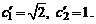 Знак в выражении для
Знак в выражении для  будет определен ниже.
будет определен ниже.
Фазовая функция  определяется полюсами нагрузки (зна-
определяется полюсами нагрузки (зна-
чениями  , при которых
, при которых  обращается в бесконечность). Задан-
обращается в бесконечность). Задан-
ная нагрузка имеет один полюс 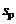 при
при  . При этом
. При этом 
 . Функция
. Функция  . Разло-жения в ряды Лорана указанных функций имеют следующий вид:
. Разло-жения в ряды Лорана указанных функций имеют следующий вид:
|
|
|

 ,
, 
 .
.
Входящий во второе уравнение физической реализуемости коэффициент  есть вычет
есть вычет  относительно полюса нагрузки
относительно полюса нагрузки  , который является также нулем передачи
, который является также нулем передачи  .
.
Из первого уравнения условия физической реализуемости  следует, что в выражении для
следует, что в выражении для  нужно взять знак минус. Из второго уравнения
нужно взять знак минус. Из второго уравнения  следует
следует
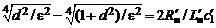 .
.
Вторым необходимым для нахождения неизвестных параметров аппроксимации условием является условие оптимальности СЦ по критерию максимума полосы согласования. Для того чтобы учесть это условие, выразим из уравнения физической реализуемости  :
:
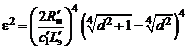
и подставим в  :
:
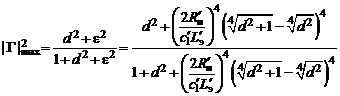 .
.
Выражая из этого равенства  через заданное
через заданное  и
и  , получим функцию
, получим функцию
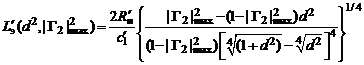 .
.
Оптимальное значение  определяется из уравнения [7, с. 319]
определяется из уравнения [7, с. 319]
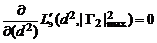 и равно
и равно  .
.
Затем определяется оптимальное значение 
 .
.
Значения  и
и  могут быть также получены из табл. 4.1 [1, с. 60]
могут быть также получены из табл. 4.1 [1, с. 60]
с учетом того, что 
4. По найденным параметрам аппроксимации  и
и  определяем коэффициенты полиномов числителя и знаменателя
определяем коэффициенты полиномов числителя и знаменателя  и получившуюся максимально возможную величину
и получившуюся максимально возможную величину  :
:
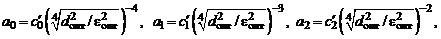
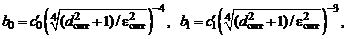
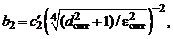
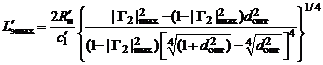 .
.
Максимально возможная полоса согласования при заданных качестве согласования и параметрах нагрузки легко определяется из найденного значения  . По определению
. По определению  . Отсюда
. Отсюда  , а нижняя и верхняя частоты полосы согласования
, а нижняя и верхняя частоты полосы согласования
|
|
|
 .
.
5. Далее по найденному выражению  определяем входное сопротивление цепи (рис. 3) относительно точек подключения нагрузки [6, с. 70]
определяем входное сопротивление цепи (рис. 3) относительно точек подключения нагрузки [6, с. 70]
 .
.
6. По найденной функции  методом Кауэра синтезируем СЦ. Для этого дробно-рациональную функцию
методом Кауэра синтезируем СЦ. Для этого дробно-рациональную функцию  разлагаем в цепную дробь [2, с. 34]
разлагаем в цепную дробь [2, с. 34]
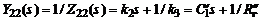 .
.
Получившееся расчетное сопротивление генератора  , как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации
, как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации  .
.
В результате синтеза приходим к низкочастотному эквиваленту согласующей цепи (см. рис. 4, а).
7. Производим денормировку элементов и преобразуем НЧ эквивалент цепи в полосовую согласующую цепь (рис. 4, б):
 .
.
Если  , то
, то 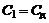 , а
, а  отсутствует. Если же
отсутствует. Если же  , то
, то 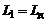 , а
, а  отсутствует. Величины
отсутствует. Величины  и
и 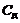 определены на первом этапе расчета.
определены на первом этапе расчета.
На этом расчет заканчивается.
Дата добавления: 2018-02-15; просмотров: 655; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
