Теория широкополосного согласования Юлы
Постановка задачи согласования по методу Юлы. Условия физической реализуемости согласующей цепи и их математическая формулировка. Нули передачи и их классификация. Определение физически реализуемой функции входного иммитанса, структуры и параметров элементов согласующей цепи. Примеры синтеза согласующих цепей по методу Юлы.
Методические указания
Теория Юлы базируется на понятии нуля передачи и уравнении физической реализуемости. Нулем передачи являются нули функции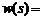 
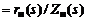, лежащие в правой полуплоскости и на мнимой оси, а уравнением физической реализуемости является
.
Здесь 
– фазовая функция, которая определяется полюсами 
, а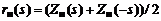 
. Нули передачи в теории Юлы делятся на четыре класса. Признаками отнесения нуля к тому или иному классу являются место расположения нуля на комплексной плоскости (в правой полуплоскости или на мнимой оси) и значение модуля сопротивления нагрузки в нуле передачи (нуль, конечное значение или бесконечность). Математической формулировкой условий физической реализуемости СЦ являются системы равенств, в которые входят коэффициенты разложения в ряды Лорана фазовой функции и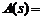 
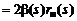, полностью определяемые параметрами нагрузки, и коэффициенты ряда Лорана для 
, в которые входят неизвестные параметры аппроксимации 
и 
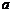(или 
и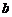 
). В простейшем случае простого нуля передачи при 
или 
условие физической реализуемости дает одно уравнение. Второе уравнение получается из условия оптимальности СЦ. Оптимизация цепи осуществляется теми же способами, что и в методе Боде–Фано. Из полученных уравнений находят оптимальные параметры аппроксимации 
и 
(или 
и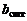 
), что дает возможность определить коэффициенты полиномов числителя и знаменателя , затем входное сопротивление 
и осуществить синтез СЦ.
|
|
|
Литература: [2, с. 67–76; 5, с. 152–156].
Вопросы для самопроверки
1. Изложите исходные предпосылки и сформулируйте задачу согласования по методу Юлы.
2. Поясните понятие нуля и класса нуля передачи в теории Юлы.
3. Как определяется в теории Юлы фазовая функция ?
3. Что является условиями физической реализуемости согласующей цепи в теории Юлы?
4. Изложите последовательность решения задачи широкополосного согласования по методу Юлы.
Решение задачи согласования
С помощью теории колебательных контуров
Основные положения теории одиночных и связанных колебательных контуров. Одиночный контур и его параметры. Канонические структуры системы связанных контуров. Коэффициент связи, приведенная добротность, парциальные контуры и их параметры. Оценка потенциальных возможностей согласования комплексной нагрузки с помощью теории связанных контуров. Выбор типа, структуры и определение параметров элементов согласующей цепи.
|
|
|
Методические указания
При изучении материала этого раздела курса необходимо уяснить основные понятия теории одиночных и связанных контуров. Исходной при решении задачи согласования при этом является частотная характеристика модуля коэффициента передачи системы связанных контуров. Из этой характеристики при наложении определенных условий определяется минимальное значение максимума коэффициента стоячей волны как функция полосовой добротности нагрузки. Это соотношение, позволяющее оценить потенциальные возможности согласования комплексной нагрузки цепью с конечным числом элементов, может быть получено для полиномиальной и оптимальной СЦ при чебышевской и максимально плоской характеристиках рабочего затухания.
Определение параметров элементов согласующей цепи в виде системы связанных контуров производится с использованием понятия парциальных контуров системы и формул для определения резонансной частоты, добротности, характеристического сопротивления и коэффициента связи между контурами.
|
|
|
Литература: [2, с. 76–90].
Вопросы для самопроверки
1. Поясните понятия характеристического сопротивления, резонансной частоты, добротности, резонансного сопротивления и частотной характеристики коэффициента передачи одиночных последовательного и параллельного контуров.
2. Как определяются приведенная добротность, коэффициент связи и парциальные контуры для системы двух связанных контуров?
3. Какой параметр нагрузки определяет потенциальные возможности ее согласования?
4. В чем различия полиномиальных и оптимальных согласующих цепей?
5. Изложите последовательность определения параметров элементов на конкретном примере двухзвенной согласующей цепи.
Заключение
Состояние теории и проблемы широкополосного согласования комплексных нагрузок.
Литература: [2, с. 90].
Вопросы для самопроверки
1. В чем состоит проблема широкополосного согласования сложных комплексных нагрузок?
Дата добавления: 2018-02-15; просмотров: 918; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!