II. КОНТРОЛЬНОЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ
УКАЗАНИЯ ДЛЯ ЕГО ВЫПОЛНЕНИЯ
Контрольное задание
Произвести расчет двухзвенной согласующей цепи комплексной нагрузки по методам Боде–Фано и Юлы. Исходные данные для расчета приведены в табл. 1. Вид аппроксимации частотных характеристик СЦ для расчета по методу Боде–Фано задан в последнем столбце таблицы. Для расчета согласующей цепи по методу Юлы следует взять другую из двух возможных аппроксимацию. Заданная параметрами ее эле-
ментов нагрузка последовательного типа (последовательное соединение  и
и  ). Способ расчета (на наилучшее качество согласо-
). Способ расчета (на наилучшее качество согласо-
вания или на максимум полосы) зависит от исходных данных таблицы. Если в таблице заданы  , то расчет производится на минимум
, то расчет производится на минимум  , т.е. на наилучшее качество согласования в заданной полосе.
, т.е. на наилучшее качество согласования в заданной полосе.
Т а б л и ц а 1
| Номер варианта | fн, ГГц | fв, ГГц | f0, ГГц | | Г |max | Rн, Ом | Lн, нГн | Сн, пФ | Rг, Ом | Вид аппроксимации |
| 1 | 0.4 | 0.6 | – | – | 5 | 3.9 | 40.0 | 75 | тейлор. |
| 2 | – | – | 0.8 | 0.20 | 4 | 3.2 | 15.0 | 75 | тейлор. |
| 3 | 0.8 | 1.0 | – | – | 6 | 4.6 | 8.5 | 50 | чебыш. |
| 4 | – | – | 0.9 | 0.18 | 3 | 2.4 | 18.0 | 50 | чебыш. |
| 5 | 1.0 | 1.2 | – | – | 5 | 3.8 | 6.8 | 75 | тейлор. |
| 6 | – | – | 1.0 | 0.16 | 2 | 1.6 | 18.3 | 75 | тейлор. |
| 7 | 1.3 | 1.5 | – | – | 4 | 3.0 | 5.6 | 50 | чебыш. |
| 8 | – | – | 1.1 | 0.18 | 3 | 2.2 | 6.4 | 50 | чебыш. |
| 9 | 1.6 | 1.8 | – | – | 5 | 3.6 | 2.2 | 75 | тейлор. |
| 10 | - | – | 1.2 | 0.15 | 4 | 3.0 | 5.3 | 75 | тейлор. |
| 11 | 1.9 | 2.1 | – | – | 5 | 4.0 | 2.5 | 50 | чебыш. |
| 12 | – | – | 1.3 | 0.20 | 3 | 2.5 | 5.1 | 50 | чебыш. |
| 13 | 0.7 | 0.9 | – | – | 6 | 4.9 | 7.1 | 75 | тейлор. |
| 14 | – | – | 1.4 | 0.22 | 5 | 3.7 | 5.8 | 75 | тейлор. |
| 15 | 1.1 | 1.3 | – | – | 3 | 2.3 | 6.0 | 50 | чебыш. |
| 16 | – | – | 1.5 | 0.20 | 4 | 3.3 | 5.4 | 50 | чебыш. |
| 17 | 0.9 | 1.1 | – | – | 3 | 2.1 | 18.0 | 75 | тейлор. |
| 18 | – | – | 1.6 | 0.25 | 5 | 3.1 | 5.4 | 75 | тейлор. |
|
|
|
Если же заданы  и
и  , то расчет производится на максимум полосы согласования при заданном качестве согласования. Заданный в таблице способ расчета следует применить при расчете СЦ методом Боде–Фано. Для расчета СЦ по методу Юлы следует взять другой из двух возможных. При этом
, то расчет производится на максимум полосы согласования при заданном качестве согласования. Заданный в таблице способ расчета следует применить при расчете СЦ методом Боде–Фано. Для расчета СЦ по методу Юлы следует взять другой из двух возможных. При этом  или
или  и
и  следует взять из результатов расчета по методу Боде–Фано.
следует взять из результатов расчета по методу Боде–Фано.
Методические указания
Перед выполнением контрольной работы следует изучить теоретический материал курса. Исходные данные для расчетов сведены в табл. 1. Номер варианта задания определяется как сумма двух последних цифр номера зачетной книжки. Целью расчетов является определение структуры и параметров элементов согласующей цепи.
По каждому из методов расчета СЦ (Боде–Фано и Юлы) возможны четыре варианта расчета: на максимальное значение полосы согласования  при заданном качестве согласования и на минимум
при заданном качестве согласования и на минимум 
в заданной полосе  при максимально плоской и чебышевской частотных характеристиках рабочего затухания СЦ. Все эти варианты расчетов имеют свои особенности и рассмотрены ниже.
при максимально плоской и чебышевской частотных характеристиках рабочего затухания СЦ. Все эти варианты расчетов имеют свои особенности и рассмотрены ниже.
|
|
|
Вариант расчета 1. Метод Боде–Фано.
Максимально плоская аппроксимация.
Расчет на наилучшее качество согласования
В заданной полосе
В этом случае заданы нижняя и верхняя частоты полосы согласования 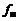 ,
,  , параметры нагрузки и выходное сопротивление генератора. Расчет может быть проведен в следующей последовательности.
, параметры нагрузки и выходное сопротивление генератора. Расчет может быть проведен в следующей последовательности.
1. Достроим нагрузку до резонанса на средней частоте полосы согласования. Для этого определим среднюю частоту заданной полосы  и резонансную частоту нагрузки
и резонансную частоту нагрузки  . Если
. Если  , то последовательно с нагрузкой включают дополнительную индуктивность
, то последовательно с нагрузкой включают дополнительную индуктивность  , где
, где  . Если же
. Если же  , то достройка нагрузки до резонанса на частоте
, то достройка нагрузки до резонанса на частоте  осуществляется последовательным включением дополнительной емкости
осуществляется последовательным включением дополнительной емкости  , где
, где  . Вначале проведем расчет низкочастотного (НЧ) эквивалента СЦ с последующим преобразованием низкочастотного эквивалента в полосовую СЦ. При этом в качестве НЧ эквивалента нагрузки следует взять
. Вначале проведем расчет низкочастотного (НЧ) эквивалента СЦ с последующим преобразованием низкочастотного эквивалента в полосовую СЦ. При этом в качестве НЧ эквивалента нагрузки следует взять 
 , если
, если 

 , если
, если 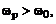 и Rн. Емкость нагрузки будет восстановлена при преобразовании НЧ эквивалента СЦ в полосовую цепь.
и Rн. Емкость нагрузки будет восстановлена при преобразовании НЧ эквивалента СЦ в полосовую цепь.
|
|
|
2. Осуществим нормировку элементов  и
и  относительно
относительно  и частоты среза низкочастотного эквивалента СЦ
и частоты среза низкочастотного эквивалента СЦ  . При этом
. При этом 
 . Штрихами помечены нормированные элементы.
. Штрихами помечены нормированные элементы.
3. Определим оптимальные значения параметров аппроксимации  и
и  из условий физической реализуемости СЦ и наилучшего качества согласования (минимального значения
из условий физической реализуемости СЦ и наилучшего качества согласования (минимального значения  ) в заданной полосе. Реактивный четырехполюсник нагрузки (рис.1) имеет простой нуль передачи при
) в заданной полосе. Реактивный четырехполюсник нагрузки (рис.1) имеет простой нуль передачи при  , так как при
, так как при  сопротивление индуктивности нагрузки бесконечно велико и от генератора в
сопротивление индуктивности нагрузки бесконечно велико и от генератора в  мощность не проходит. Это дает одно условие физической реализуемости
мощность не проходит. Это дает одно условие физической реализуемости  . Здесь
. Здесь  и
и  – коэффициенты разложения функций
– коэффициенты разложения функций  и
и  в ряды Лорана в нуле передачи, а
в ряды Лорана в нуле передачи, а  и
и  – коэффициенты отражения в сечении подключения
– коэффициенты отражения в сечении подключения  при наличии и отсутствии СЦ соответственно (рис. 1, а и б).
при наличии и отсутствии СЦ соответственно (рис. 1, а и б).

а б
Рис.1
Коэффициент  зависит исключительно от параметров нагрузки и в данном случае равен
зависит исключительно от параметров нагрузки и в данном случае равен  . Коэффициент
. Коэффициент  определяется функцией
определяется функцией  , которая для двухзвенной цепи задается отношением полиномов второй степени
, которая для двухзвенной цепи задается отношением полиномов второй степени
|
|
|
 .
.
Коэффициенты полиномов числителя и знаменателя  выражаются через параметры аппроксимации
выражаются через параметры аппроксимации  и
и  , и в данном случае тейлоровской аппроксимации они равны [6, с. 40]
, и в данном случае тейлоровской аппроксимации они равны [6, с. 40]

Здесь  принимает значения
принимает значения 
 – коэффициенты стандартных по-линомов Баттерворта. Для
– коэффициенты стандартных по-линомов Баттерворта. Для  (двухзвенная СЦ)
(двухзвенная СЦ) 

Выполняя разложение функции  , получим условие физической реализуемости СЦ [2, с. 59]
, получим условие физической реализуемости СЦ [2, с. 59]
 .
.
Вторым необходимым для нахождения неизвестных параметров аппроксимации условием является условие оптимальности СЦ по критерию минимума  . Для того чтобы учесть это условие, выразим из уравнения физической реализуемости
. Для того чтобы учесть это условие, выразим из уравнения физической реализуемости  :
:

и подставим это выражение в выражение для  . В результате получим
. В результате получим  как функцию одной переменной
как функцию одной переменной  :
:
 .
.
Оптимальное значение  определяется из условия [7, с. 319]
определяется из условия [7, с. 319]

Это уравнение не разрешается относительно  . Вместе с тем для практически важных случаев малых
. Вместе с тем для практически важных случаев малых  с достаточной для практики
с достаточной для практики
точностью  может быть определено из приближенного выражения
может быть определено из приближенного выражения

Оптимальное значение  находят с помощью полученного выше из условия физической реализуемости выражения и известного значения
находят с помощью полученного выше из условия физической реализуемости выражения и известного значения  .
.
Точные значения  и
и  могут быть определены из табл. 4.1 [2, с. 60].
могут быть определены из табл. 4.1 [2, с. 60].
4. По известным параметрам аппроксимации  и
и  определяем коэффициенты полиномов числителя и знаменателя
определяем коэффициенты полиномов числителя и знаменателя  и получившееся минимально возможное значение масимума модуля коэффициента отражения:
и получившееся минимально возможное значение масимума модуля коэффициента отражения:

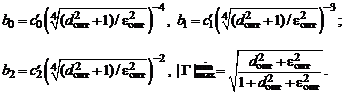
5. Далее по найденному выражению для  определяем нормированное входное сопротивление цепи относительно точек подключения
определяем нормированное входное сопротивление цепи относительно точек подключения  (рис. 2):
(рис. 2):
 .
.
Здесь  .
.
6. Затем по найденной функции  методом Кауэра синтезируем СЦ. Для этого дробно-рациональную функцию
методом Кауэра синтезируем СЦ. Для этого дробно-рациональную функцию  разлагаем в цепную дробь [2, с. 34]:
разлагаем в цепную дробь [2, с. 34]:
 .
.
Получившееся расчетное сопротивление генератора  , как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации
, как правило, не равно заданному. Поэтому на входе СЦ следует включить идеальный трансформатор с коэффициентом трансформации  .
.
В результате синтеза приходим к низкочастотному эквиваленту СЦ (рис. 2, а).

а б
Рис. 2
7. Производим денормировку элементов и преобразуем низкочастотный эквивалент цепи в полосовую СЦ (рис. 2, б):
 .
.
Если  , то
, то 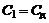 , а
, а  . Если же
. Если же  , то
, то 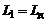 , а
, а  (отсутствует). Величины
(отсутствует). Величины  и
и 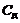 определены на первом этапе расчета.
определены на первом этапе расчета.
На этом расчет заканчивается.
Дата добавления: 2018-02-15; просмотров: 706; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
