Метод поиска с использованием кубичной аппроксимации
В соответствии с рассматриваемым методом подлежащая минимизации функция f аппроксимируется полиномом третьего порядка. Логическая схема метода аналогична схеме методов с использованием квадратичной аппроксимации. Однако в данном случае построение аппроксимирующего полинома проводится на основе меньшего числа точек, поскольку в каждой точке можно вычислять значения как функции, так и ее производной.
Работа алгоритма начинается в произвольно выбранной точке  : находится другая точка
: находится другая точка 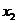 , такая, что производные
, такая, что производные 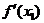 и
и  имеют различные знаки. Другими словами, необходимо заключить стационарную точку
имеют различные знаки. Другими словами, необходимо заключить стационарную точку , в которой
, в которой  , в интервал между
, в интервал между  и
и 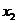 Аппроксимирующая кубичная функция записывается в следующем виде:
Аппроксимирующая кубичная функция записывается в следующем виде:

Параметры уравнения (2.8) подбираются таким образом, чтобы значения  и ее производной в точках
и ее производной в точках  и
и 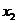 совпадали со значениями f(x) и f'(x) в этих точках. Первая производная функции
совпадали со значениями f(x) и f'(x) в этих точках. Первая производная функции  равна
равна

Коэффициенты  из уравнения (2.8) определяются по известным значениям
из уравнения (2.8) определяются по известным значениям  путем решения следующей системы линейных уравнений:
путем решения следующей системы линейных уравнений:

Заметим, что данная система легко решается рекурсивным методом. После того как коэффициенты найдены, действуя по аналогии со случаем квадратичной аппроксимации, можно оценить координату стационарной точки функции / с помощью аппроксимирующего полинома (2.8). При этом приравнивание к нулю производной (2.9) приводит к квадратному уравнению. Используя формулу для вычисления корней квадратного уравнения, запишем решение, определяющее стационарную точку аппроксимирующего кубичного полинома, в следующем виде:
|
|
|

где

Формула для  обеспечивает надлежащий выбор одного из двух корней квадратного уравнения; для значений
обеспечивает надлежащий выбор одного из двух корней квадратного уравнения; для значений  , заключенных в интервале от 0 до 1, формула (2.10) гарантирует, что получаемая точка
, заключенных в интервале от 0 до 1, формула (2.10) гарантирует, что получаемая точка  расположена между
расположена между  и
и 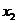 . Затем снова выбираются две точки для реализации процедуры кубичной аппроксимации —
. Затем снова выбираются две точки для реализации процедуры кубичной аппроксимации —  ; и одна из точек
; и одна из точек  или
или 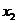 , причем значения производной исследуемой функции в этих точках должны быть противоположны по знаку. Процедура кубичной аппроксимации повторяется.
, причем значения производной исследуемой функции в этих точках должны быть противоположны по знаку. Процедура кубичной аппроксимации повторяется.
Приведем формализованное описание алгоритма. Пусть заданы начальная точка 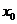 , положительная величина шага
, положительная величина шага  и параметры сходимости
и параметры сходимости  и
и  .
.
Шаг 1. Вычислить  .
.
Если 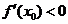 , вычислить
, вычислить  для значений k=0,1,2…
для значений k=0,1,2…
Если  , вычислить
, вычислить  для значений k=0,1,2…,
для значений k=0,1,2…,
Шаг 2. Вычислить значения  в точках
в точках  при k=0,1,2…, вплоть до точки
при k=0,1,2…, вплоть до точки  , в которой
, в которой  . Затем положить
. Затем положить  ,
,  . Вычислить значения
. Вычислить значения  .
.
Шаг 3. Найти стационарную точку  аппроксимирующего кубичного полинома, пользуясь формулой (2.10).
аппроксимирующего кубичного полинома, пользуясь формулой (2.10).
Шаг 4. Если  , перейти к шагу 5. В противном случае вычислять
, перейти к шагу 5. В противном случае вычислять  по формуле
по формуле  до тех пор, пока не будет выполняться неравенство
до тех пор, пока не будет выполняться неравенство  .
.
|
|
|
Шаг 5. Проверка на окончание поиска.
Если  и
и  , поиск закончить.В противномслучае положить либо
, поиск закончить.В противномслучае положить либо

либо

затем перейти к шагу 3.
Заметим, что шаги 1 и 2 реализуют процедуру поиска границ интервала по эвристическому методу, причем изменение знака производной используется в качестве критерия перехода через точку оптимума. На шаге 3 проводятся вычисления координаты точки оптимума аппроксимирующего полинома. Шаг 4 ассоциирован с проверкой того факта, что полученная оценка действительно является улучшенным приближением к точке оптимума. В случае, когда значения производной вычисляются непосредственно, метод поиска с использованием кубичной аппроксимации, безусловно, оказывается более эффективным по сравнению с любым из представленных выше методов поиска. Однако если значения производной вычисляется путем разностного дифференцирования, то предпочтение следует отдать методу Пауэлла, основанному на квадратичной аппроксимации.
Пример 2.8
Минимизировать функцию  , используя Метод кубичной аппроксимации и производных (начальная точка
, используя Метод кубичной аппроксимации и производных (начальная точка  , длина шага
, длина шага  ,
,  ).
).

Итерация 1.
Шаг 1.  . Следовательно,
. Следовательно,  .
.
Шаг 2.  .
.
Так как  , стационарная точка расположена между точками 1 и 2. Положим
, стационарная точка расположена между точками 1 и 2. Положим  . Тогда
. Тогда  .
.
|
|
|
Шаг 3.

Шаг 4.  . Следовательно, продолжаем поиск.
. Следовательно, продолжаем поиск.
Шаг 5. Проверка на окончание поиска.
 . Поиск не закончен, так как
. Поиск не закончен, так как  , положим
, положим 
Итерация 2.
Шаг 3

Шаг 4.  . Следовательно, продолжаем поиск.
. Следовательно, продолжаем поиск.
Шаг 5. Проверка на окончание поиска:

Поиск закончен.
Заметим, что при тех же самых исходных точках  метод Пауэлла в примере 2.9 позволил получить оценку
метод Пауэлла в примере 2.9 позволил получить оценку  , тогда как метод с использованием кубичной аппроксимации привел к оценке
, тогда как метод с использованием кубичной аппроксимации привел к оценке  . Точная координата точки минимума равна 1.5874, что указывает на преимущество полиномиальной аппроксимации более высокого порядка.
. Точная координата точки минимума равна 1.5874, что указывает на преимущество полиномиальной аппроксимации более высокого порядка.
Сравнение методов
С помощью теоретических выкладок можно показать, что такие методы точечного оценивания, как метод Пауэлла или метод поиска с использованием кубичной аппроксимации и производных, существенно эффективнее методов исключения интервалов, среди которых выделяется метод золотого сечения. В частности, известно, что применение схемы поиска с использованием квадратичной аппроксимации позволяет достигнуть асимптотически суперлинейной скорости сходимости к точке истинного минимума, т. е. отклонение (k+1)-й оценки от истинной координаты точки минимума пропорционально отклонению k-й оценки, возведенному в степень a>1 (как показано в [6], a=1,3). Для сравнения отметим, что если при реализации метода золотого сечения в качестве k-й оценки координаты точки истинного минимума берется координата средней точки интервала, полученного в результате k вычислений значения функции, то отклонение этой оценки от точной координаты линейно убывает при переходе от k-й к (k+1)-й итерации. Это означает, что в случае, когда интервалы сходимости сравнимы между собой, метод, основанный на квадратичной аппроксимации, сходится быстрее, чем любой из методов исключения интервалов. Разумеется, сделанный вывод справедлив лишь в предположении, что интервалы сходимости сравнимы между собой, а исследуемая функция является достаточно гладкой и унимодальной.
|
|
|
Результаты численных экспериментов, представленные в специальной литературе, не подтверждают преимущества методов с использованием производных и квадратичной аппроксимации или метода исключения интервалов над остальными методами. Если для вычисления значений целевой функции требуется значительное машинное время, то, по мнению авторов работы [7], предпочтительнее использовать стратегию поиска, основанную на модификации метода Пауэлла. Это мнение подтверждается результатами вычислительных экспериментов, проведенных Химмельблау [8], который сравнил указанную стратегию поиска со схемой поиска по методу золотого сечения и показал, что модифицированный метод Пауэлла требует меньшего количества вычислений значения функции для достижения заданной точности при оценивании координаты точки минимума. Если необходимо получить решение с очень высокой степенью точности, то лучшими оказываются методы поиска на основе полиномиальной аппроксимации. С другой стороны, известно, что при исследовании мультимодальных или быстро изменяющихся функций метод Пауэлла сходится значительно медленнее, чем методы исключения интервалов. Таким образом, если очень важно добиться надежной работы алгоритма, то целесообразно выбрать метод золотого сечения. Поэтому поисковые методы типа метода Пауэлла следует использовать совместно с методом золотого сечения, переход, к алгоритму которого осуществляется в тех случаях, когда реализация соответствующих итераций на ЭВМ связана с определенными трудностями. В книге Брента [9] проведен анализ относительной эффективности различных методов поиска.
Сравнительное исследование трех методов точечного оценивания, а именно метода средней точки, метода Пауэлла и метода поиска с использованием кубичной аппроксимации, было проведено в соответствии с учебной программой по университетскому (Purdue University) курсу теории оптимизации. Перечисленные методы использовались для решения задачи минимизации функции  при различных значениях k. Кроме того, для сравнения был также использован метод золотого сечения как наилучший из методов исключения интервалов.
при различных значениях k. Кроме того, для сравнения был также использован метод золотого сечения как наилучший из методов исключения интервалов.
Для оценки эффективности выбранных методов использовались три характеристики: время, затраченное на получение решения, точность решения и чувствительность к изменениям параметра сходимости. Первые две характеристики исследовались путем варьирования значений показателя степени k на множестве нечетных чисел от 1 до 79. Следует отметить, что для всех значений k минимум функции достигается в точке х* =4,71239; при этом f(x*)=-1,0. Однако с увеличением k степень гладкости функции, которая обладает узкими впадинами в окрестности точки минимума, уменьшается. Это обстоятельство приводит к понижению точности и замедлению сходимости методов точечного оценивания.
Проверка методов на чувствительность проводилась путем варьирования значений параметра сходимости. Как и ожидалось, в результате исследований установлена тенденция к увеличению затрат времени на решение задачи с ростом k, которая особенно ярко проявляется при реализации метода средней точки вследствие резкого увеличения модуля градиента функции в окрестности точки минимума. Однако возрастание показателя степени k не оказывает заметного влияния на продолжительность поиска с помощью метода золотого сечения. Аналогично точность решения, измеряемая как относительная (в процентах) ошибка оценивания координаты точки истинного минимума, падает с ростом k для всех трех методов - метода средней точки, метода Пауэлла и метода поиска с использованием кубичной аппроксимации. Однако метод золотого поиска оказывается весьма нечувствительным к изменениям крутизны функции. Исследования также показали, что чувствительность всех четырех выбранных методов к изменениям параметра сходимости минимальна.
Заключение
В главе были рассмотрены необходимые и достаточные условия оптимальности решения задач безусловной оптимизации с целевыми функциями одной переменной.
Показано, что необходимое условие наличия оптимума в данной точке заключается в том что данная точка должна быть стационарной, т. е. первая производная функции должна обращаться в нуль в этой точке. Для того чтобы проверить, соответствует ли стационарная точка минимуму, максимуму или является точкой перегиба, используются производные второго и более высоких порядков.
Рассмотрены вопросы, связанные с получением оптимальных решений на основе методов поиска, которые носят название методов исключения интервалов и ориентированы на нахождение точки оптимума в заданном интервале. Показано, что алгоритм поиска по методу золотого сечения является наиболее предпочтительным вследствие высокой вычислительной эффективности и простоты реализации.
Методы исключения интервалов основаны па процедуре простого сравнения значений функции в двух пробных точках; при таком сравнении используется только отношение порядка на множестве значений функции. Для того чтобы учесть величину разности между значениями функции, разработан ряд так называемых методов точечного оценивания, позволяющих определить точку оптимума с помощью квадратичной или кубичной аппроксимации целевой функции. В условиях, когда выполняется предположение о том, что интервалы сходимости сравнимы между собой, а исследуемая функция является достаточно гладкой и унимодальной, методы точечного оценивания сходятся значительно быстрее, чем методы исключения интервалов. Однако при исследовании мультимодальных или быстро изменяющихся функций наиболее надежным оказывается метод золотого сечения.
В заключение сформулированы рекомендации, в соответствии с которыми методы поиска с использованием квадратичной аппроксимации типа метода Пауэлла, вообще говоря, следует применять совместно с методом золотого сечения, переход к алгоритму которого реализуется в тех случаях, когда выполнение соответствующих итерационных циклов на ЭВМ сопряжено с определенными трудностями.
Контрольные вопросы и задачи
2.1. Что такое точка перегиба и как ее идентифицировать?
2.2. Как проверить, является ли функция выпуклой или вогнутой?
2.3. В чем состоит свойство унимодальности функций и в чем заключается важное значение этого свойства при решении задач оптимизации с одной переменной?
2.4. Пусть данная точка удовлетворяет достаточным условиям существования локального минимума. Как установить, является ли этот минимум глобальным?
2.5. Сформулируйте условие, при выполнении которого метод поиска, основанный на полиномиальной интерполяции, может не привести к получению правильного решения.
2.6. Являются ли методы исключения интервалов в целом более эффективными, чем методы точечного оценивания? Почему?
2.7. При реализации поисковых методов рекомендуется принимать решение об окончании поиска на основе проверок как величины разности значений переменной, так и величины разности значений функции. Возможна ли ситуация, когда результат одной из проверок указывает на сходимость к точке минимума, тогда как полученная точка в действительности минимуму не соответствует? Поясните ответ рисунком.
2.8. Заданы следующие функции одной переменной:

Для каждой из заданных функций найдите
(1) интервал (ы) возрастания, убывания;
(2) точки перегиба (если таковые имеются);
(3) интервал(ы), в котором (в которых) функция вогнута, выпукла;
(4) локальные и глобальный максимумы (если таковые имеются);
(5) локальные и глобальный минимумы (если таковые имеются).
2.9. Паром, который должен курсировать через канал, конструируется с таким расчетом, чтобы с его помощью можно было перевозить заданное количество груза в тоннах (L) в течение дня (Рис. 2.16).
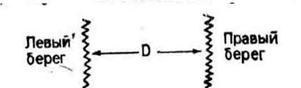
Рис. 2.16. Схема к задаче 2.9
Пусть стоимость парома без двигателей прямо пропорциональна грузоподъемности парома (l), а стоимость двигателей прямо пропорциональна произведению грузоподъемности на скорость движения парома (v) в кубе. Покажите, что полная стоимость парома минимальна в том случае, когда стоимость парома без двигателей в два раза превышает стоимость двигателей. (Временем погрузки и разгрузки можно пренебречь, т. е. считается, что паром курсирует без остановок.)
2.10. Лесной пожар распространяется в узкой долине шириной 2 мили со скоростью 32 фут/мин (Рис. 2.17). Содержать наступление огня можно путем построения заградительной противопожарной перегородки, пересекающей лес по всей ширине долины. Один рабочий может построить 2 фута перегородки в минуту. Затраты на транспортировку каждого рабочего к месту событий и обратно составляют 20 долл.; оплата труда каждого рабочего составляет 6 долл. в час. Стоимость квадратной мили леса равна 2000 долл. Сколько рабочих следует послать на борьбу с огнем, чтобы полные издержки были минимальны?

Рис. 2.17. Схема к задаче 2.10
2.11. Рассмотрите задачу безусловной оптимизации с целевой функцией одной переменной f(x). Пользуясь приведенными в таблице данными о значениях производных порядка 1, 2, 3, 4 в точках Xi (i==l, 2, . . . , 10), идентифицируйте каждую из точек (установите, оказывается ли она точкой максимума, минимума, перегиба или не является точкой оптимума; укажите случаи, когда нельзя сделать определенный вывод и т. д.).

| 
| 
| 
| 
|
| X1 | 0 | + | Нет данных | Нет данных |
| X2 | 0 | 0 | + | Нет данных |
| X3 | 0 | - | Нет данных | Нет данных |
| X4 | - | - | Нет данных | Нет данных |
| X5 | 0 | 0 | - | Нет данных |
| X6 | 0 | 0 | 0 | - |
| X7 | 0 | 0 | 0 | 0 |
| X8 | 0 | 0 | 0 | + |
| X9 | + | + | Нет данных | Нет данных |
| X10 | 0 | - | + | - |
2.12. Установите, какие из следующих функций являются выпуклыми или вогнутыми.

2.13. Исследуйте функцию

Найдите локальные минимумы, локальные максимумы, глобальный минимум и глобальный максимум f в заданном интервале.
2.14. Установитеобласти, в которых следующая функция выпукла или вогнута:

Найдите глобальный максимум и глобальный минимум этой функции.
2.15. Рассмотрите модель одного цикла управления запасами скоропортящихся товаров, в которой спрос описывается случайной величиной с плотностью вероятности f, т. е. Р (величина спроса £ х) =  ;
;
отсутствие запасов влечет за собой экономические потери;
С — стоимость единицы товара;
р — величина потерь, обусловленных отсутствием запасов (включая потери дохода и так называемого неосязаемого основного капитала);
r — продажная цена единицы товара;
l — ликвидационная стоимость единицы товара,не проданного к концу периода.
Задача заключается в том, чтобы определить оптимальный размер заказа Q, который максимизирует ожидаемую величину чистого дохода за период. Ожидаемый чистый доход равен

где  —ожидаемая величина спроса.
—ожидаемая величина спроса.
(а) Покажите, что II(Q)—выпуклая функция Q(³0).
(б) Объясните, как определить оптимальный размер заказа, пользуясь результатом, полученным в п. (а).
(в) Вычислите оптимальный размер заказадля следующегоконкретного примера:
С=2,50 долл., г=5,00 долл., l=0, р=2,50 долл., f(х)=1/400 при 100£х£500 и f(х)=0 в противномслучае.
Указание. Воспользуйтесь правилом Лейбница для дифференцирования под знаком интеграла.
2.16. Предположим, что проводится одномерный поиск на основе (а) метода золотого сечения и (б) метода средней точки с использованием производных, вычисляемых с помощью разностного дифференцирования. Какой из методов, по всей вероятности, окажется более эффективным? Почему?
2.17. Реализуйте процедуру одномерного поиска точки оптимума функции, используя (а) метод золотого сечения, (б) метод деления интервала пополам, (в) метод поиска с использованием квадратичной аппроксимации, (г) метод поиска с использованием кубичной аппроксимации и производных.

В каждом случае проведите по четыре вычисления значения функции. Сравните результирующие интервалы поиска, полученные с помощью перечисленных выше методов.
2.18. Найдите точку минимума функции

Заданы начальная точка х=2 и длина шага D=0.5.
(а) Воспользуйтесь методом исключения интервалов: поиск границ интервала эвристическим методом и шесть итераций по методу золотого сечения.
(б) Воспользуйтесь методом оценивания на основе квадратичной аппроксимации: три итерации по методу Пауэлла.
2.19. Найдите вещественные корни уравнения (с точностьюдоодного знака после запятой)

используя (а) метод Ньютона — Рафсона, (б) метод средней точки, (в) метод секущих.
2.20. (а) Объясните, как можно преобразовать задачу 2.19 в нелинейную задачу безусловной оптимизации с одной переменной. (б) Напишите программу для ЭВМ, реализующую поиск по методу золотого сечения, и используйте ее для решения задачи оптимизации, о которой идет речь в п. (а). Сравните полученное решение с решением задачи 2.19.
2.21. В результате экспериментов установлено, что траектория движения космического тела описывается следующим уравнением [10]:
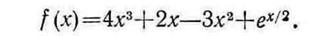
Найдите корень уравнения f(x)=0 с помощью любого из методов с использованием производных.
Д.22. Пользуясь любым из методов одномерного поиска, минимизируйте следующие функции с точностью до одного знака после запятой [10]:

2.23. В структуре капитальных вложений на развитие химического завода важное место занимают затраты на приобретение и монтаж труб, а также затраты на установку насосного оборудования. Рассмотрите проект трубопровода длиной L фут., который должен обеспечивать подачу жидкости со скоростью Q галлон/мин. Выбор наиболее экономичного диаметра трубы D (дюйм.) осуществляется на основе минимизации функции затрат на приобретение труб, насосов и прокачивание жидкости. Известно, что функция затрат в единицу времени в случае, когда трубопровод состоит из труб, изготовленных из углеродистой стали, и центробежного насоса с электродвигателем, может быть описана следующим выражением:

Сформулируйте соответствующую задачу оптимизации с одной переменной для проектирования трубопровода длиной 1000 фут., который должен обеспечивать подачу жидкости со скоростью 20 галлон/мин. Диаметр трубы должен быть заключен в пределах от 0,25 до 6 дюйм. Решите эту задачу с помощью метода золотого сечения.
Литература
1. Swarm W. H., Report on tlie Development of A Direct Search Method of Optimization, ICI Ltd., Central Instr. Res. Lab., Res. Note, 64/3, London, 1964.
2. Kiefer J., Optimum Sequential Search and Approximation Methods Under Minimum Regularity Assumptions, /. Soc. fnd. Appl. Math., 5(3), 105—125 (1957).
3. Bartle R., Elements of Real Analysis, Wiley, N.Y„ 1976.
4. Powell M. J. D., An Efficient Method for Finding the Minimum of a Function of Several Variables Without Calculating Dzrivatives, Computer J., 7, 155—162 (1964).
5. RaphsonJ., History of Fluxion, London, 1725.
6. Kowalik J., Osboruc M. R., Methods for Unconstrained Optimization Problems, American Elscvicr, N. Y., 19G8.
7. Box M. J., Davies D., Swann W. H., Nonlinear Optimization Techniques, I.C. I. Monograph, Oliver and Boyd, Edinburgh, 1969.
8. Himmelblau D. M.: Applied Nonlinear Programming, McGraw-Hill, N. Y., 1972. {Имеется перевод: Химмельблау' Д. M. Прикладное нелинейное программирование.—M., Мир, 1975.1
9. Brent R. P., Algorithms for Minimization without Derivatives, Prentice-Hall, Englewood Cliffs, New Jersey, 1973.
10. Phillips D.Т., Ravindran A., Solbcrg J.J., Operations Research: Principles and Practice, Wiley, N. Y., 1976.
[1] Британская тепловая единица; 1 БТЕ == 252 кал
[2] В отечественной литературе этот метод известен по названием "метод хорд"
Дата добавления: 2018-02-15; просмотров: 1447; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
