Этап установления границ интервала
На этом этапе сначала выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно поиск граничных точек такого интервала проводится с помощью эвристических методов поиска, хотя в ряде случаев можно также использовать методы экстраполяции. В соответствии с одним из эвристических методов, который был предложен Свенном [I], (k+1)-я пробная точка определяется по рекуррентной формуле
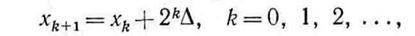
где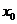 
- произвольно выбранная начальная точка, 
— подбираемая некоторым способом величина шага. Знак определяется путем сравнения значений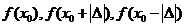 
. Если
то, согласно предположению об унимодальности, точка минимума должна располагаться правее точки 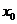и величина выбирается положительной. Если изменить знаки неравенств на противоположные,то следует выбирать отрицательной. Еслиже
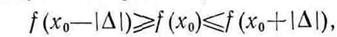
то точка минимума лежит между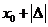 
и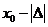 
и поиск граничных точек завершен. Случай, когда
противоречит предположению об унимодальности. Выполнение этого условия свидетельствует о том, что функция не является унимодальной.
Пример 2.1
Установить границы интервала в задаче минимизации функции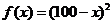 
при заданной начальной точке 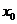=30 и величине шага =5.
Знак определяется на основе сравнения значений
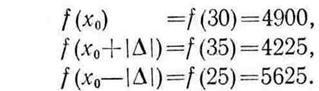
Так как
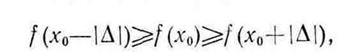
то величина должна быть положительной, а координата точки минимума х* должна быть больше 30. Имеем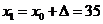 
. Далее 
, 
,
|
|
|
откуда х*>35.
,
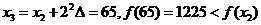откуда х*>45.
,
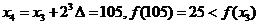откуда х*>65.
,
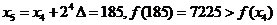следовательно, х*<185. Таким образом, шесть шагов вычислений х* позволили выявить интервал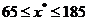 
, в котором расположена точка х*. Заметим, что эффективность поиска граничных точек непосредственно зависит от величины шага . Если велико, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если мало, для определения граничных точек может потребоваться достаточно большой объем вычислений.
Этап уменьшения интервала
После того как установлены границы интервала, содержащего точку оптимума, можно применить более сложную процедуру уменьшения интервала поиска с целью получения уточненных оценок координат оптимума. Величина подынтервал, исключаемого на каждом шаге, зависит от расположения пробных точек 
и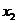 
внутри интервала поиска. Поскольку местонахождение точки оптимума априори неизвестно, целесообразно предположить, что размещение пробных точек должно обеспечивать уменьшение интервала в одном и том же отношении. Кроме того, в целях повышения эффективности алгоритма необходимо потребовать, чтобы указанное отношение было максимальным. Подобную стратегию иногда называют минимаксной стратегией поиска.
|
|
|
Дата добавления: 2018-02-15; просмотров: 986; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!