Пример 2.4. Задача управления запасами

⇐ ПредыдущаяСтр 6 из 12Следующая ⇒

Многие фирмы создают запасы производимых товаров для удовлетворения, будущего спроса. Среди причин, обусловливающих содержание запасов в определенном объеме, можно отметить нерациональные потери времени и средств, связанные с их непрерывным пополнением. С другой стороны, пополнение запасов через продолжительные промежутки времени приводит к образованию чрезмерно больших запасов, которое требует необоснованных капитальных затрат и значительно повышает стоимость хранения запасов. Определение оптимального объема запасов представляет собой классическую задачу оптимизации, для решения которой часто используется так называемая модель определения наиболее экономичного размера заказа.

В рамках этой модели спрос предполагается постоянным и равным единиц товара в год. Частое пополнение запасов нецелесообразно, так как стоимость выполнения одного заказа составляет К долл. независимо от его размера. Первоначальная стоимость единицы товара равна с долл. Хранение излишних запасов также нецелесообразно, поскольку стоимость хранения единицы товара отлична от нуля и составляет h долл. в год. Для того чтобы упростить задачу, предположим, что спрос удовлетворяется немедленно (т. е. одолженные заказы отсутствуют), а пополнение осуществляется сразу же, как только запасы иссякают.

Рис. 2.9 иллюстрирует изменение объема запасов с течением времени. В точке А объем запасов равен В, затем объем запасов начинает уменьшаться со скоростью единиц товара в единицу времени и достигает нулевого значения в точке С. В это время поступает новая партия товара, и объем запасов восстанавливается.

Треугольник АВС представляет один цикл управления запасами, который повторяется во времени. Задача заключается в том, чтобы определить оптимальный размер заказа В и продолжительность интервала времени между заказами С—А. Обозначим соответствующие переменные через Q и Т.

Поскольку Т есть величина промежутка времени, в течение которого при скорости расходования К истощается запас Q, имеем T==Q/l. Таким образом, задача сводится к нахождению оптимального значения Q. Заметим, что когда Q мало, переменная Т также принимает малое значение. При этом частота заказов велика, что обусловливает большие затраты на выполнение заказов и относительно малые издержки хранения запасов.

Рис. 2.9. Циклы управления запасами

С другой стороны, наличие большого объема запасов (Q велико) приводит к увеличению затрат на хранение запасов и одновременно к снижению издержек, связанных с выполнением заказов на товары. Одна из основных задач управления запасами состоит в определении оптимального значения Q, которому соответствует минимум суммы полных годовых затрат.

Получим аналитическое выражение для функции полных годовых затрат (затраты/цикл х количество циклов/год).

Количество циклов (заказов)/год=1/Т==l/Q,

Затраты/цикл = Затраты па выполнение заказов +

+ Затраты на хранение запасов =

=(K+cQ)+[(Q/2)hT]=

=K+cQ+(hQ²/2l).

Примечание. Затраты на хранение запасов в течение цикла равны затратам на хранение Q/2 единиц товара в течение интервала времени Т.

Таким образом, подлежащая минимизации функция полных затрат есть

Отсюда следует, что f(Q) — выпуклая функция и если существует положительное значение Q*, такое, что f'(Q*)=0, то Q* минимизирует f(Q).

Решив уравнение f'(Q)=0, получим

Таким образом, оптимальный размер заказа равен

При этом Т*=(2K/hl)^0.5 - интервал времени между заказами. Величина Q* известна в теории управления запасами как наиболее экономичный размер заказа.

Методы исключения интервалов

В разд. 2.2 рассматривался вопрос анализа "в статике", который заключается в том, чтобы определить, является ли данное решение оптимальным. Для этого были построены необходимые и достаточные условия оптимальности решения. Далее мы переходим к изучению вопроса анализа "в динамике", связанного с нахождением оптимального решения. С этой целью ниже рассматривается ряд одномерных методов поиска, ориентированных на нахождение точки оптимума внутри заданного интервала. Методы поиска, которые позволяют определить оптимум функции одной переменной путем последовательного исключения подынтервалов и, следовательно, путем уменьшения интервала поиска, носят название методов исключения интервалов.

В разд. 2.1 было дано определение унимодальной функции. Унимодальность функций является исключительно важным свойством. Фактически все одномерные методы поиска, используемые на практике, основаны на предположении, что исследуемая функция в допустимой области, по крайней мере, обладает свойством унимодальности. Полезность этого свойства определяется тем фактом, что для унимодальной функции f(x) сравнение значений f(x) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точка оптимума отсутствует.

Теорема 2.3

Пусть функция f унимодальна на замкнутом интервале а£х£b, а ее минимум достигается в точке х*. Рассмотрим точки х₁ и х₂,. расположенные в интервале таким образом, что а<х₁<х₂<b. Сравнивая значения функции в точках х₁ и х₂ можно сделать следующие выводы.

1. Если , то точка минимума f(x) не лежит в интервале ( ), т. е. (рис. 2.10).

2. Если , то точка минимума не лежит в интервале ( ), т. е. (см. рис. 2.10).

Доказательство

Рассмотрим случай, когда . Пусть утверждение теоремы неверно, т. е. . Поскольку х* - точка минимума, то по определению f(x*)£f(x) для всех 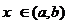. Получаем двойное неравенство

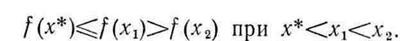
Это неравенство не может выполняться, так как унимодальная функция f(x) должна быть монотонной по обе стороны от точки х*. Таким образом, получено противоречие, доказывающее утверждение теоремы. Аналогичные рассуждения справедливы также в случае, когда .

Рис. 2.10. Графические иллюстрации к теореме 2.3.

Примечание.

Если , то можно исключить оба крайних интервала ( ) и ( ); при этом точка минимума должна располагаться в интервале ( ).

Согласно теореме 2.3, которую иногда называют правилом исключения интервалов, можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило исключения интервалов, устраняет необходимость полного перебора всех допустимых точек. Несомненным достоинством поисковых методов такого рода является то что они основаны лишь на вычислении значений функций. При этом не требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значений функции f (х) в заданных точках х с помощью прямых расчетов или имитационных экспериментов. Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:

этап установления границ интервала,на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума;

этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины.

Дата добавления: 2018-02-15; просмотров: 836; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!