Свойства функций одной переменной

⇐ ПредыдущаяСтр 5 из 12Следующая ⇒

Согласно наиболее простому определению, функция f(x) представляет собой правило, которое позволяет каждому значению х поставить в соответствие единственное значение y=f(x). В этом случае х носит название независимой переменной, а у — зависимой переменной. Рассмотрим множество , где R — множество всех действительных чисел. Мы можем определить соответствие (или преобразование), с помощью которого каждой точке 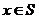придается единственное числовое значение. Такое соответствие называется скалярной функцией f, определенной на множестве S.

Когда множество S=R, мы имеем дело со всюду определенной функцией одной переменной. Если S есть некоторое подмножество множества R, то функция f определена в ограниченной области.

Например,

есть всюду определенная функция, тогда как функция

определена в ограниченной области. В теории оптимизации f называется целевой функцией, а S — допустимой областью, множеством точек, удовлетворяющих ограничениям, или областью допустимых значений х.

Ряд физических процессов можно описать (или построить модели этих процессов) с помощью непрерывных функций, т. е. функций, которые обладают свойством непрерывности в каждой точке x_i, принадлежащей областям их определения.

Рис. 2.1. Разрывная функция

Однако в инженерных приложениях нередки и такие случаи, когда приходится использовать разрывные функции. Например, если мы строим график функции, которая измеряет затраты на сообщение некоторой системе количества тепла, равного 1 БТЕ [1], при различных температурах системы, то в результате получаем кусочно-непрерывную кривую, изображенную на рис. 2.1. Затраты описываются разрывной функцией температуры системы; однако температура системы может принимать все значения в диапазоне от 200 до 3000 градусов по шкале Фаренгейта.

Разумеется, не всегда необходимо, чтобы область допустимых значений независимой переменной х содержала все действительные числа из рассматриваемого интервала. Вполне возможны случаи, когда переменная принимает только дискретные значения. Например, если мы строим график функции, представляющей зависимость стоимости погонного фута трубы от ее диаметра, то естественно ограничиться линии последовательностью точек, изображенных на рис. 2.2, поскольку количество установленных размеров выпускаемых промышленностью труб конечно.

Примечание. Важно иметь в виду, что непрерывные функции обладают следующими свойствами:

1) сумма или произведение непрерывных функций является непрерывной функцией;

2) отношение двух непрерывных функций является функцией, непрерывной во всех точках, в которых знаменатель отношения не обращается в нуль.

Очевидно, что в зависимости от того, является ли исследуемая функция непрерывной или разрывной, а также в зависимости от структуры допустимой области для реализации процедуры поиска точек оптимума функции следует использовать различные методы. Необходимо отметить, что метод, эффективный при анализе непрерывных функций, может оказаться неэффективным при исследовании разрывных функций, хотя обратное не исключается.

Рис. 2.2. Дискретная функция

В дополнение к перечисленным выше свойствам можно также классифицировать функции в соответствии с их формой, определяющей топологические свойства функций в рассматриваемом интервале.

Рис. 2.3. Монтонно возрастающая функция.

Рис. 2.4. Монотонно убывающая функция.

Монотонные функции. Функция f(x) является монотонной (как при возрастании, так и при убывании), если для двух произвольных точек и 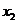таких, что выполняется одно из следующих неравенств:

На рис. 2.3 представлен график монотонно возрастающей функции, а на рис. 2.4 — график монотонно убывающей функции. Заметим, что монотонная функция не обязательно должна быть непрерывной. На рис. 2.5 изображен график функции, которая монотонно убывает при 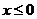и монотонно возрастает при . Функция достигает своего минимума в точке х=х* (начале координат) и монотонна по обе стороны от точки минимума. Такие функции называются унимодальными.

Рис. 2.5. Унимодальная функция.

Определение

Функция f (х) является унимодальной на отрезке 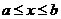в том и только том случае, если она монотонна по обе стороны от единственной на рассматриваемом интервале оптимальной точки х*. Другими словами, если х*— единственная точка минимума f(x) на отрезке 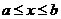, то f(x) оказывается унимодальной на данном интервале тогда и только тогда, когда для точек и

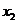
Непрерывная Разрывная Дискретная

Рис. 2.6. Унимодальные функции.

Как показано на рис. 2.6, унимодальная функция не обязательно должна быть непрерывной. Унимодальность функций является исключительно важным свойством, которое широко используется в оптимизационных исследованиях. Вопросы, связанные с этим свойством функций, рассматриваются в разд. 2.3.

Критерии оптимальности

При анализе оптимизационных задач, как правило, возникают два общих вопроса.

1. Вопрос анализа «в статике». Как определить, представляет ли данная точка х* оптимальное решение задачи?

2. Вопрос анализа «в динамике». Если х* не является точкой оптимума, то какая последовательность действий приводит к получению оптимального решения?

В этом разделе основное внимание уделяется решению вопроса диализа «в статике», а именно построению множества критериев оптимальности, позволяющих определить, является ли данное решение оптимальным.

Определения.

Функция f(x), определенная на множестве S, достигает своего глобального минимума в точке в том и только том случае, если

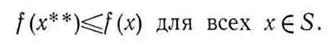
Функция f(x), определенная на множествеS, имеет локальный минимум (относительный минимум) в точке 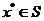в том и только том случае, если

для всех х, удаленныхот х* на расстояние, меньшее ,т. е. если существует , такое, что для всех х, удовлетворяющих условию , выполняется неравенство .

Замечания

1. Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный.

2. Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.

Рис. 2.7. Локальные и глобальные оптимумы.

3. Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов; при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.

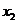На рис. 2.7 точка — точка глобального максимума, — точка локального минимума, — точка локального максимума, — точка глобального минимума, а Хь можно рассматривать и как точку локального минимума, и как точку локального максимума.

Идентификация оптимумов в случае функции одной переменной.

Предположим, что функция f (х) одной переменной х определена на открытом интервале (а, b) и n-кратно дифференцируема на этом интервале. Если х*— внутренняя точка интервала, то теорема Тейлора позволяет записать изменение функции f при переходе от точки х* к точке ( ) в следующем виде:

где через обозначена сумма членов, в которых степень равна (n+1) и выше. Если х*— локальный минимум функции f на (а, b), то по определению должна существовать -окрестность точки x*, такая, что для всех х из этой окрестности выполняется неравенство

Из неравенства (2.2) следует, что

При достаточно малом первое слагаемое доминирует над остальными, а так как можно выбрать и положительным, и отрицательным, то неравенство (2.3) будет выполняться только в том случае, если

Рассуждая аналогичным образом, нетрудно установить, что неравенство (2.3) будет справедливым только тогда, когда

Эта же схема анализа применима и в случае локального максимума, с той лишь разницей, что знак неравенства (2.2) требуется заменить на противоположный. Мы получили следующий общий результат, который можно сформулировать в виде теоремы.

Теорема2.1

Необходимые условия того, что х* является точкой локального минимума (максимума) дважды дифференцируемой функции f на открытом интервале (а, b), выражаются следующими соотношениями:

Эти условия являются необходимыми, т. е. в случае, когда они не выполняются, точка х* не может быть точкой локального минимума (максимума). С другой стороны, если эти условия выполняются, мы не имеем гарантии, что х* является точкой локального минимума (максимума). Рассмотрим, например, функцию , график которой представлен на рис. 2.8. Эта функция удовлетворяет необходимым условиям наличия, как локального минимума, так и локального максимума в начале координат, однако не имеет ни максимума, ни минимума при х*=0.

Рис. 2.8. Точка перегиба.

Определения Стационарной точкой называется точка х*, в которой

Если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму),то она является точкой перегиба, или седловой точкой.

Для того чтобы провести различие между случаями, когда стационарная точка соответствует локальному минимуму, локальному максимуму или является точкой перегиба, необходимо построить достаточные условия оптимальности.

Теорема2.2

Пусть в точке первые (п—1) производные функции обращаются в нуль, а производная порядка п отлична от нуля.

(1) Если п — нечетное, то х*— точка перегиба.

(2) Если п — четное, то х*— точка локального оптимума.

Кроме того,

(а) если эта производная положительная, то х*— точка локального минимума;

(б) если эта производная - отрицательная, то х*—точка локального максимума.

Доказательство

Утверждение теоремы нетрудно доказать с помощью разложения в ряд Тейлора, представленного равенством (2.1). Поскольку порядок первой отличной от нуля производной равен n, формулу (2.1) можно переписать в следующем виде:

Если п — нечетное число, то правая часть (2.6) может принимать как положительные, так и отрицательные значения в зависимости от того, является ли величина положительной или отрицательной. Это означает, что в зависимости от знаки разность f(x^-\-v)—f(x*) либо положительная, либо отрицательная. Следовательно, функция не достигает в точке х* своею минимального или максимального значения, т.е. х* — точка перегиба.

Далее рассмотрим случай, когда п — четное число. При этом величина 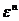всегда положительная, а знак правой части (2.6) определяется первым слагаемым, если — достаточно малая величина. Таким образом, если величина положительная, то и точка х* соответствует локальному минимуму. Аналогичные рассуждения нетрудно провести также и для локального максимума.

Для того чтобы применить теорему 2.2 к функции , график которой изображен на рис. 2.8, вычислим

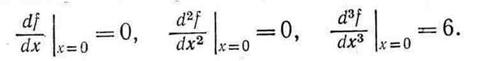
Так как порядок первой отличной от нуля производной равен 3 (нечетное число), точка х=0 является точкой перегиба.

Замечание

Выше предполагалось, что рассматриваемая функция дифференцируема или что ее первая производная существует и непрерывна. Однако если функция не является дифференцируемой во всех точках области определения, то даже необходимое условие наличия оптимума, позволяющее идентифицировать стационарные точки, может не выполняться в точке оптимума. Например, рассмотрим кусочно-линейную функцию

Эта функция непрерывна во всех точках действительной оси, но не дифференцируема при х=2. Функция достигает максимума в точке х=2, которая не является стационарной в соответствии с данным выше определением.

Пример 2.1

Рассмотрим функцию

определенную на всей действительной оси. Первая производная этой функции равна

Ясно, что первая производная обращается в нуль в точках х=0, 1,2,3, и, следовательно, эти точки можно классифицировать как стационарные. Вторая производная функции равна

Вычислив значения второй производной в четырех точках х=0, 1,2,3, получим

Отсюда следует вывод, что х=1, 3 — точки локальных минимумов, а х=2 — точка локального максимума. Чтобы идентифицировать точку х=0, вычислим третью производную

Так как эта производная отлична от нуля и имеет нечетный порядок, то точка х=0 является не точкой оптимума, а точкой перегиба.

Следующий вопрос, к рассмотрению которого мы переходим, связан с определением глобального максимума или минимума функции одной переменной. Поскольку глобальный оптимум является локальным, можно вычислить все локальные оптимумы и выбрать из них наилучший. Алгоритм, основанный на этом простейшем подходе, приводится ниже.

Максимизировать f(x) при ограничении ,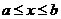

где а и b — установленные границы изменения значений переменной х.

Таккак функция исследуется на заданном интервале, нетрудно заметить, что проверку наличия локального оптимума необходимо проводить не только в стационарных точках, но и в граничных точках интервала.

Шаг 1. Приравнять df/dx=0 и найти все стационарные точки.

Шаг 2. Выбрать все стационарные точки, которые расположены в интервале [а, b]. Обозначим эти точки через .

Проверку наличия локального оптимума следует проводить только на множестве указанных точек, дополненном точками а и b.

Шаг 3. Найти наибольшее значение f (х) из множества f(a), f(b), f(х_i), . . . ,f(х_N),. Это значение соответствует глобальному максимуму.

Примечание. При построении алгоритма мы не пытались классифицировать стационарные точки как точки локального минимума, точки локального максимума или точки перегиба, поскольку для этого требуется вычисление производных высших порядков. Для определения глобального оптимума легче вычислить соответствующие значения функции и выбрать из них максимальное.

Пример 2.2 Максимизировать на интервале

Приравниваем первую производную нулю

Решая это уравнение, получаем две стационарные точки х=3 и х= -1, которые расположены внутри заданного интервала.

Для того чтобы найти глобальный максимум, вычислим значения f(x) в точках х=3, -1, -2 и 4:

Таким образом, точках=3 соответствует максимальному значению f на интервале .

Вместо перебора всех стационарных точек и соответствующих значений функции можно воспользоваться специальными процедурами, позволяющими найти глобальный оптимум с меньшими затратами времени при условии, что функция обладает определенными ' свойствами. В заключительной части разд. 2.1 было дано определение унимодальной функции, для которой локальный оптимум является глобальным. К сожалению, определение унимодальной функции не позволяет непосредственно проверить, является ли функция унимодальной. Однако в теории оптимизации выделяется важный класс унимодальных функций, а именно класс выпуклых и вогнутых функций, которые допускают проверку такого рода. Основные свойства выпуклых и вогнутых функций приведены в приложении Б.

Пример 2.3

Исследуем свойства функции

При имеем , и, следовательно, функция является вогнутой в указанной области. Если же , то , т. е. функция является выпуклой в этой области.

Заметим, что функция имеет две стационарные точки х=-0.5 и х=2.5. Поскольку , функция обладает локальным максимумом при х=-0.5. В точке х=2.5 вторая производная , и, следовательно, функция достигает в этой точке локального минимума. Если ограничить допустимую область неравенством , то f(x) имеет глобальный максимум при х=-0.5, так как f(x)— вогнутая функция (в данной области) и х=-0.5 — точка локального максимума. Аналогично если ограничить допустимую область неравенством , то f(x) достигает глобального минимума при х =2.5. Однако если переменная х изменяется на всей действительной оси от — 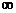до + 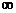, то функция f(x) не имеет конечного глобального максимума или минимума.

Дата добавления: 2018-02-15; просмотров: 1596; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!