Использование методов оптимизации для анализа и обработки информации
Еще одна широкая область применения оптимизационных методов в инженерной практике связана с задачами инженерного анализа, в частности с задачами нелинейного регрессионного анализа. Среди наиболее общих проблем, возникающих в процессе разработка инженерных моделей, можно выделить проблему определения параметров некоторой полуэмпирической модели на основе заданного множества экспериментальных данных. Такого рода задачи обработки информации, или задачи регрессионного анализа, путем несложных преобразований приводятся к виду оптимизационных задач, поскольку выбор значении параметров модели осуществляется в соответствии с критерием качества описания имеющихся данных-с помощью этой модели.
Предположим, что некоторая переменная у зависит от некоторой независимой переменной х, а связь между ними задается уравнением  , в котором фигурируют два параметра
, в котором фигурируют два параметра 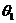 и
и  . Для того чтобы определить соответствующие значения
. Для того чтобы определить соответствующие значения 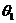 и
и  , необходимо провести серию экспериментов, в каждом из которых задается значение независимой переменной х и регистрируется значение зависимой переменной у. Результатом серии из N экспериментов является множество пар чисел (
, необходимо провести серию экспериментов, в каждом из которых задается значение независимой переменной х и регистрируется значение зависимой переменной у. Результатом серии из N экспериментов является множество пар чисел (  ), i=1, . . . , N, Затем на основе полученной информации делается попытка подобрать значения
), i=1, . . . , N, Затем на основе полученной информации делается попытка подобрать значения 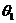 и
и  таким образом, чтобы обеспечить хорошую точность описания экспериментальных данных с помощью функции f. Наиболее часто используемая на практике мера качества описания экспериментальных данных определяется так называемым критерием наименьших квадратов, в соответствии с которым требуется минимизировать функцию
таким образом, чтобы обеспечить хорошую точность описания экспериментальных данных с помощью функции f. Наиболее часто используемая на практике мера качества описания экспериментальных данных определяется так называемым критерием наименьших квадратов, в соответствии с которым требуется минимизировать функцию
|
|
|
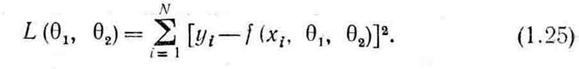
Разность  между зарегистрированным значением
между зарегистрированным значением  ; и теоретическим значением
; и теоретическим значением  показывает, насколько точно выбранная модель описывает имеющиеся данные, и называется остатком. Сумма квадратов остатков по всем экспериментальным точкам является мерой точности описания данных. Действительно, если значение
показывает, насколько точно выбранная модель описывает имеющиеся данные, и называется остатком. Сумма квадратов остатков по всем экспериментальным точкам является мерой точности описания данных. Действительно, если значение  равно нулю, то сделанный выбор
равно нулю, то сделанный выбор 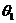 и
и  обеспечивает точное описание, поскольку экспериментальные данные совпадают с теоретической кривой. Таким образом, задачу
обеспечивает точное описание, поскольку экспериментальные данные совпадают с теоретической кривой. Таким образом, задачу
описания данных можно рассматривать как задачу оптимизации, в которой требуется найти значения параметров 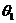 и
и  , минимизирующие функцию
, минимизирующие функцию  .
.
Пример 1.4 Нелинейная регрессия
Описание задачи. Известно, что соотношение между давлением, молярным объемом и температурой реальных газов отличается от аналогичного соотношения для идеального газа, которое записывается в виде

где Р—давление (атм), v—молярныйобъем (см3/г×моль); Т— температура (К), R - универсальная газовая постоянная (82,06 атм×см3/г моль К).
Полуэмпирическое уравнение Редлиха — Куонга[3]
|
|
|

ориентировано на то, чтобы скомпенсировать отклонение свойств реального газа от свойств идеального газа, и содержит параметры а и b, значения которых определяются на основе экспериментальных данных. В табл. 1.2 приведены результаты измерений давления, молярного объема и температуры углекислого газа (СО2), которые используются при расчете нелинейной регрессии для оценивания значений а и b.
Таблица 1.2. Результаты измерений давления, молярного объема и температуры углекислого газа

Постановка задачи. Значения параметров а и b находятся путем минимизации суммы квадратов остатков(1.25).В данном случае эта функция имеет следующий вид:

где Pi— результат измерения давления в эксперименте с номером i, а остальные два слагаемых в скобках представляют соответствующие члены уравнения (1.26) в условиях эксперимента с номером i и зависят от параметров а и b. Например, слагаемое суммы, которое соответствует первому эксперименту, равно

Функция (1.27) представляет собой функцию двух переменных, которая подлежит минимизации путем соответствующего выбора значений независимых переменных а и b. Если бы уравнение Редлиха — Куонга точно описывало имеющиеся данные, то минимальное значение функции (1.27) равнялось бы нулю. Однако наличие экспериментальных ошибок в результатах измерений, а также отдельные упрощения, принимаемые при построении уравнения, приводят к тому, что изучаемая модель лишь приближенно описывает свойства углекислого газа, и, следовательно, функция (1.27) не обращается в нуль в точке оптимума. В частности, оптимальным значениям, а=6,377*107 и b=29,7 соответствует сумма квадратов остатков, равная 9,7*10-2.
|
|
|
Кроме задач регрессионного анализа в инженерной практике возникает множество других задач, которые можно формулировать и решать как задачи оптимизации. Отметим ставший классическим подход к определению равновесного состава химической смеси [З]. Известно, что равновесным состоянием замкнутой системы, начальное состояние которой задано, при фиксированной температуре и фиксированном давлении является такое состояние, при котором свободная энергия Гиббса принимает минимальное значение. В работе [8] показано, что задача определения равновесного состава смеси может быть сформулирована как задача минимизации нелинейной функции при ограничениях, образованных системой линейных уравнений вместе с условиями неотрицательности переменных.
|
|
|
Другая классическая инженерная задача, которую можно сформулировать и решить как задачу оптимизации, связана с определением величин установившихся токов в электрической цепи, составленной из активных сопротивлений [9]. Если известны величины сопротивлений и полный ток в цепи, то значения токов через сопротивления можно определить путем решения задачи минимизации полной потери мощности в цепи (I2R) с учетом линейных ограничений, которые обеспечивают выполнение закона Кирхгофа для каждого узла цепи.
Дата добавления: 2018-02-15; просмотров: 657; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
