Полиномиальная аппроксимация и методы точечного оценивания
Применение методов исключения интервалов, которые рассматривались в предыдущем разделе, накладывает единственное требование на исследуемую функцию: она должна быть унимодальной. Следовательно, указанные методы можно использовать для анализа как непрерывных, так и разрывных функций, а также в случаях, когда переменные принимают значения из дискретного множества. Логическая структура поиска с помощью методов исключения интервалов основана на простом сравнении значений функции в двух пробных точках. Кроме того, при таком сравнении в расчет принимается только отношение порядка на множестве значений функции и не учитывается величина разности между значениями функции. В данном разделе рассматриваются методы поиска, которые позволяют учесть относительные изменения значений функции и как следствие в ряде случаев оказываются более эффективными, чем методы исключения интервалов. Однако выигрыш в эффективности достигается ценой введения дополнительного требования, согласно которому исследуемые функции должны быть достаточно гладкими.
Основная идея рассматриваемых методов связана с возможностью аппроксимации гладкой функции полиномом и последующего использования аппроксимирующего полинома для оценивания координаты точки оптимума. Необходимыми условиями эффективной реализации такого подхода являются унимодальность и непрерывность исследуемой функции. Согласно теореме Вейерштрасса об аппроксимации [З], если функция непрерывна в некотором интервале, то ее с любой степенью точности можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координату точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома. Согласно теореме Вейерштрасса, качество оценок координаты точки оптимума, получаемых с помощью аппроксимирующего полинома, можно повысить двумя способами: использованием полинома более высокого порядка и уменьшением интервала аппроксимации. Второй способ, вообще говоря, является более предпочтительным, поскольку построение аппроксимирующего полинома порядка выше третьего становится весьма сложной процедурой, тогда как уменьшение интервала в условиях, когда выполняется предположение об унимодальности функции, особой сложности не представляет.
|
|
|
Методы оценивания с использованием квадратичной аппроксимации
Простейшим вариантом полиномиальной интерполяции является квадратичная аппроксимация, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть, по крайней мере, квадратичной. Если же функция линейная, то ее оптимальное значение может достигаться только в одной из двух граничных точек интервала. Таким образом, при реализации метода оценивания с использованием квадратичной аппроксимации предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенную аппроксимационную схему для оценивания координаты точки истинного минимума функции.
|
|
|
Если задана последовательность точек 
и известны соответствующие этим точкам значения функции 
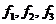,- то можно определить постоянные величины 
таким образом, что значения квадратичной функции
совпадут со значениями f(х) в трех указанных точках. Перейдем к вычислению q (x) в каждойиз трех заданных точек. Прежде всего, так как
имеем 
. Далее, поскольку
получаем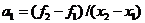 
.
Наконец, при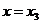 
Разрешая последнее уравнение относительно 
получаем
Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры и из аппроксимирующего квадратичного полинома с помощью приведенных выше формул.
Если точность аппроксимации исследуемой функции в интервале от 
до 
с помощью квадратичного полинома оказывается достаточно высокой, то в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координаты точки оптимума. Напомним, что стационарные точки функции одной переменной определяются путем приравнивания к нулю ее первой производной и последующего нахождения корней полученного таким образом уравнения. В данном случае из уравнения
|
|
|
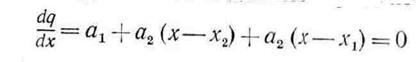
можно получить
Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина 
окажется приемлемой оценкой координаты точки истинного оптимумал;*.
Пример 2.4
Рассчитать координату точки минимума функции 
при использовании квадратичной аппроксимации в интервале 
.
Пусть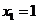 
, 
, а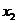 
есть средняя точка интервала, т. е. 
. Вычислим соответствующие значения функции:
Для того чтобы оценить , необходимо найти значения параметров 
и аппроксимирующей функции. Имеем
Подстановка этих значений в формулу для позволяет получить
Точный минимум достигается при 
=1.5874.
|
|
|
Дата добавления: 2018-02-15; просмотров: 804; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!