Метод последовательного оценивания с использованием квадратичной аппроксимации
Этот метод, разработанный Пауэллом [4], основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схему алгоритма можно описать следующим образом. Пусть  - начальная точка,
- начальная точка,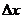 - выбранная величина шага по оси х.
- выбранная величина шага по оси х.
Шаг 1. Вычислить  .
.
Шаг 2. Вычислить  и
и  .
.
Шаг 3. Если  , положить
, положить  . Если
. Если 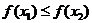 , положить
, положить  .
.
Шаг 4. Вычислить  и найти
и найти
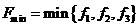
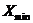 =точка
=точка  , которая соответствует
, которая соответствует  .
.
Шаг 5. По трем точкам  вычислить
вычислить  , используя формулу для оценивания с помощью квадратичной аппроксимации.
, используя формулу для оценивания с помощью квадратичной аппроксимации.
Шаг 6. Проверка на окончание поиска.
(a) Является ли разность  достаточно малой?
достаточно малой?
(б) Является ли разность  достаточно малой?
достаточно малой?
Если оба условия выполняются, закончить поиск. В противном случае перейти к шагу 7.
Шаг 7. Выбрать «наилучшую» точку ( 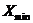 или
или  ) две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
) две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
Заметим, что при первой реализации шага 5 границы интервала, содержащего точку минимума, не обязательно оказываются установленными. При этом полученная точка  может находитьсязаточкой
может находитьсязаточкой  . Для того чтобы исключить возможность слишком большого экстраполяционного перемещения, следует провести после шага 5 дополнительную проверку и в случае, когда точка
. Для того чтобы исключить возможность слишком большого экстраполяционного перемещения, следует провести после шага 5 дополнительную проверку и в случае, когда точка  находится слишком далеко от
находится слишком далеко от  , заменить
, заменить  точкой, координата которой вычисляется с учетом заранее установленной длины шага.
точкой, координата которой вычисляется с учетом заранее установленной длины шага.
Пример 2.5
Минимизировать функцию  , используя метод Пауэлла
, используя метод Пауэлла
|
|
|
Пусть начальная точка 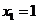 и длина шага
и длина шага  . Для проверкинаокончание поиска используются следующие параметры сходимости:
. Для проверкинаокончание поиска используются следующие параметры сходимости:
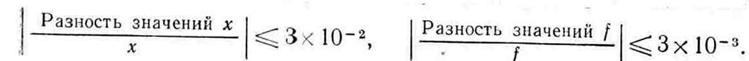
Итерация 1
Шаг 1.  .
.
Шаг 2.  .
.
Шаг 3.  , следовательно,положить
, следовательно,положить .
.
Ш а г 4. 
Шаг 5.

Ш а г 6. Проверка на окончание поиска:
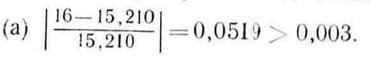
Следовательно, продолжаем поиск.
Шаг 7. Выбираем  как «наилучшую» точку, a
как «наилучшую» точку, a 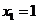 и
и  - как точки, которые ее окружают. Обозначаем, эти точки в естественном порядке и переходим к итерации 2, которая начинается с шага 4.
- как точки, которые ее окружают. Обозначаем, эти точки в естественном порядке и переходим к итерации 2, которая начинается с шага 4.
Итерация 2
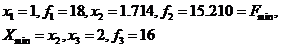
Ш а г 5.

Ш а г 6. Проверка на окончание поиска:
(а)  (условие не выполняется).
(условие не выполняется).
Шаг 7. Выбираем  как «наилучшую» точку, a
как «наилучшую» точку, a  — как точки, которые ее окружают.
— как точки, которые ее окружают.
Итерация 3.
Шаг 4.

Шаг 5.

Шаг 6. Проверка на окончание поиска:
(а  ,
,
(б 
Следовательно, поиск закончен.
Методы с использованием производных
Все рассмотренные в предыдущих разделах методы поиска основываются на предположениях об унимодальности и в ряде случаев о непрерывности исследуемой целевой функции. Целесообразно предположить, что если в дополнение к условию непрерывности ввести требование дифференцируемости функции, то эффективность поисковых процедур можно существенно повысить. Напомним, что в разд. 2.2 установлено необходимое условие существования локального минимума функции в некоторой точке z, согласно которому первая производная функции в точке z должна обращаться в нуль, т.е. 
|
|
|
Если функция f(x) содержит члены, включающие х в третьей и более высоких степенях, то непосредственное получение аналитического решения уравнения  может оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска стационарной точки функции
может оказаться затруднительным. В таких случаях используются приближенные методы последовательного поиска стационарной точки функции  . Прежде всего, опишем классическую поисковую схему, ориентированную на нахождение корня нелинейного уравнения. Эта схема была разработана Ньютоном и позднее уточнена Рафсоном [5].
. Прежде всего, опишем классическую поисковую схему, ориентированную на нахождение корня нелинейного уравнения. Эта схема была разработана Ньютоном и позднее уточнена Рафсоном [5].
Метод Ньютона — Рафсона
В рамках схемы Ньютона - Рафсона предполагается, что функция  дважды дифференцируема. Работа алгоритма начинается в точке
дважды дифференцируема. Работа алгоритма начинается в точке  , которая представляет начальное приближение (или начальную оценку) координаты стационарной точки, или корня уравнения
, которая представляет начальное приближение (или начальную оценку) координаты стационарной точки, или корня уравнения  . Затем строится линейная аппроксимация функции f'(x) в точке
. Затем строится линейная аппроксимация функции f'(x) в точке  , и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.
, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.

Рис. 2.13. Метод Ньютона — Рафсона (сходимость)
Если точка 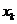 принята в качестве текущего приближения к стационарной точке, то линейная функция, аппроксимирующая функцию f'(x) в точке
принята в качестве текущего приближения к стационарной точке, то линейная функция, аппроксимирующая функцию f'(x) в точке 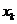 записывается в виде
записывается в виде
|
|
|
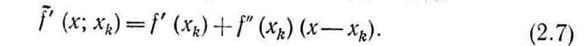
Приравняв правую часть уравнения (2.7) нулю, получим следующее приближение:

Рис. 2.13 иллюстрирует основные шаги реализации метода Ньютона. К сожалению, в зависимости от выбора начальной точки и вида функции алгоритм может, как сходиться к истинной стационарной точке, так и расходиться, что отражено на Рис. 2.14. Если начальная точка расположена правее 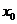 , то получаемые в результате последовательных приближений точки удаляются от стационарной точки z.
, то получаемые в результате последовательных приближений точки удаляются от стационарной точки z.

Рис. 2.14. Метод Ньютона — Рафсона (отсутствие сходимости).
Пример 2.6
Пример 2.10.
Минимизировать функцию  при
при 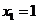 , используя Метод Ньютона — Рафсона.
, используя Метод Ньютона — Рафсона.
Для того чтобы определить стационарную точку функции f(x), воспользуемся методом Ньютона—Рафсона, положив 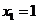 :
:

Итерации продолжаются до тех пор, пока не будет выполняться неравенство  , где
, где  —заранее установленная величина допустимого отклонения.
—заранее установленная величина допустимого отклонения.
Метод средней точки
Если функция f(x) унимодальна в заданном интервале поиска, то точкой оптимума является точка, в которой f'(х)=0. Если при этом имеется возможность вычислять как значения функции, так и се производной, то для нахождения корня уравнения  можно воспользоваться эффективным алгоритмом исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Например, если в точке z выполняется неравенство
можно воспользоваться эффективным алгоритмом исключения интервалов, на каждой итерации которого рассматривается лишь одна пробная точка. Например, если в точке z выполняется неравенство  , то с учетом предположения об унимодальности естественно утверждать, что точка минимума не может находиться левее точки z. Другими словами, интервал
, то с учетом предположения об унимодальности естественно утверждать, что точка минимума не может находиться левее точки z. Другими словами, интервал  подлежит исключению. С другой стороны, если
подлежит исключению. С другой стороны, если  , то точка минимума не может находиться правее z и интервал
, то точка минимума не может находиться правее z и интервал  можно исключить. Приведенные рассуждения лежат в основе логической структуры метода средней точки, который иногда называют поиском Больцано.
можно исключить. Приведенные рассуждения лежат в основе логической структуры метода средней точки, который иногда называют поиском Больцано.
|
|
|
Определим две точки L и R таким образом,  и
и  . Стационарная точка расположена между L и R. Вычислим значение производной функции в средней точке рассматриваемого интервала
. Стационарная точка расположена между L и R. Вычислим значение производной функции в средней точке рассматриваемого интервала  . Если
. Если  , то интервал (z, R) можно исключить из интервала поиска. С другой стороны, если
, то интервал (z, R) можно исключить из интервала поиска. С другой стороны, если  ,то можно исключить интервал (L, z). Ниже дается формализованное описание шагов алгоритма.
,то можно исключить интервал (L, z). Ниже дается формализованное описание шагов алгоритма.
Пусть имеется ограниченный интервал 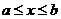 и задан параметр сходимости
и задан параметр сходимости  .
.
Шаг 1. Положить R=b, L=a при этом f'(а)<.0 и f'(b)>0.
Шаг 2. Вычислить  и f'(z).
и f'(z).
Шаг 3. Если  , закончить поиск. В противном случае, если
, закончить поиск. В противном случае, если  , положить L=z и перейти к шагу 2. Если
, положить L=z и перейти к шагу 2. Если  положить R-=z и перейти к шагу 2.
положить R-=z и перейти к шагу 2.
Следует отметить, что логическая структура поиска в соответствии с изложенным методом исключения интервалов основана лишь на исследовании знака производной независимо от значений, которые эта производная принимает. В следующем подразделе рассматривается метод секущих [2], при реализации которого рассматриваются как знак производной, так и ее значения.
Метод секущих (хорд)
Метод секущих, являющийся комбинацией метода Ньютона и общей схемы исключения интервалов, ориентирован на нахождение корня уравнения  в интервале (а, b), если, разумеется, такой корень существует.
в интервале (а, b), если, разумеется, такой корень существует.

Рис. 2.15. Метод секущих
Предположим, что в процессе поиска стационарной точки функции f(x) в интервале (а, b) обнаружены две точки L и R, в которых знаки производной различны. В этом случае алгоритм метода секущих позволяет аппроксимировать функцию f'(x) «секущей прямой» (прямой линией, соединяющей две точки) и найти точку, в которой секущая графика f'(x) пересекаетось абсцисс (Рис. 2.15). Таким образом, следующее приближение к стационарной точке  определяется по формуле
определяется по формуле

Если  , поиск следует закончить. В противном случае необходимо выбрать одну из точек L или R таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на Рис. 2.15, в качестве двух следующих точек должны быть выбраны точки z и R. Легко видеть, что в отличие от метода средней точки метод секущих основан на исследовании не только знака, но и значений производной в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска (см. Рис. 2.15).
, поиск следует закончить. В противном случае необходимо выбрать одну из точек L или R таким образом, чтобы знаки производной в этой точке и точке z были различны, а затем повторить основной шаг алгоритма. Например, в ситуации, изображенной на Рис. 2.15, в качестве двух следующих точек должны быть выбраны точки z и R. Легко видеть, что в отличие от метода средней точки метод секущих основан на исследовании не только знака, но и значений производной в пробных точках и поэтому в ряде случаев позволяет исключить более половины интервала поиска (см. Рис. 2.15).
Пример 2.7
Минимизировать функцию  в интервале
в интервале  , используя Метод секущих
, используя Метод секущих

Итерация 1.
Шаг 1.  .
.
Шаг 2
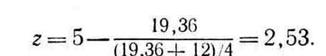
Шаг 3.  ; положить R=2.53.
; положить R=2.53.
Итерация 2.
Шаг 2

Шаг 3.  ; положить R=1.94.
; положить R=1.94.
Итерации продолжаются до тех пор, пока не будет выполняться неравенство  .
.
Дата добавления: 2018-02-15; просмотров: 971; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
