Сравнение методов исключения интервалов
Ниже проводится сравнение относительных эффективностей рассмотренных методов исключения интервалов. Обозначим длину исходного интервала неопределенности через 
, а длину интервала, получаемого в результате N вычислений значений функции,— через 
. В качестве показателя эффективности того или иного метода исключения интервалов введем в рассмотрение характеристику относительного уменьшения исходного интервала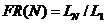 
. Напомним, что при использовании метода деления интервала пополам и метода золотого сечения длина получаемого интервала составляет 
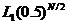и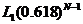 
соответственно. Следовательно, относительное уменьшение интервала после N вычислений значений функции равно
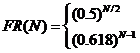
| для метода деления интервала пополам; для метода золотого сечения. |
Для сравнения рассмотрим также метод равномерного поиска, в соответствии с которым оценивание функции проводится в N равноотстоящих друг от друга точках (при этом интервал Li делится на (N+1) равных интервалов длины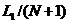 
). Пусть х* - точка, в которой наблюдается минимум функции 
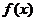. Тогда точка истинного минимума f(x) оказывается заключенной в интервале
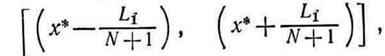
откуда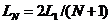 
. Следовательно, для метода равномерного поиска
.
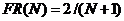В табл. 2.1 представлены значения FR (N), соответствующие выранным N, для трех методов поиска.
Таблица 2.1. Величины относительного уменьшения интервала
| Метод поиска | Количество вычислений значений функции | ||||
| N=2 | N=5 | N=10 | N=15 | N=20 | |
| Метод деления интервала пополам | 0.5 | 0.177 | 0.031 | 0.006 | 0.0009 |
| Метод золотого сечения | 0.618 | 0.146 | 0.013 | 0.001 | 0.0001 |
| Метод равномерного поиска | 0.667 | 0.333 | 0.182 | 0.125 | 0.095 |
Из таблицы следует, что поиск с помощью метода золотого сечения обеспечивает наибольшее относительное уменьшение исходного интервала при одном и том же количестве вычислений значений функции. С другой стороны, можно также сравнить количества вычислений значения функции, требуемые для достижения заданной величины относительного уменьшения интервала или заданной степени точности. Если величина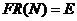 
задана, то значение N вычисляется по следующим формулам:
|
|
|
для метода деления интервала пополам
,
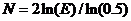для метода золотого сечения
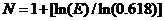б
для метода равномерного поиска
.
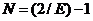В табл.2.2 приведены данные о количествах вычислений значений функции, необходимых для определения координаты точки минимума с заданной точностью.
Таблица 2.2. Требуемые количества вычислений значений функции
| Метод поиска | Количество вычислений значений функции | |||
| Е=0.1 | Е=0.05 | Е=0.01 | Е=0.001 | |
| Метод деления интервала пополам | 7 | 9 | 14 | 20 |
| Метод золотого сечения | 6 | 8 | 11 | 16 |
| Метод равномерного поиска | 19 | 39 | 199 | 1999 |
Следует еще раз подчеркнуть, что метод золотого сечения оказывается более эффективным по сравнению с остальными двумя методами, поскольку он требует наименьшего числа оцениваний значения функции для достижения одной и той же заданной точности.
|
|
|
Дата добавления: 2018-02-15; просмотров: 969; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!