Электромагнитная индукция (ЭИ)

 ЭИ – это явл, состоящее в том, что изменяющееся м. п. создаёт в замкн. проводниках эл. токи. ЭДС, возб-щую эти токи, наз-ют ЭДС индукции, а токи – индукционными (М. Фарадей в 1831 г)

Опыты Фарадея:

1)На дерев. катушку были намотаны изолированным медным проводом 2 одинак. обмотки. Концы 1 обмотки присоед-сь к тангенс-гальванометру, концы 2 – к хим. ист-ку тока (к батарее из элементов Вольты) ч/з ключ При замык ключа стрелка г-метра откл-сь на короткое время в одну сторону, при размык. – в др. 2)Повторяет 1-й с той разницей, что обмотки намат-сь на замк. железный сердечник По сравнению с дерев. катушкой эффект значительно усиливался. Этот опыт считается решающим.3)Повторяет 1-й с той разницей, что обмотки намат-сь на картонную трубку. Если трубка пустая, эффект такой же, как в первом опыте. Если в трубку опускался желез. стержень, эффект усиливался. Если опускался мед. стержень, эффект по сравнению с 1-ым опытом практически не изменялся.4)Повторяет 3-й с той разницей, что ключ обмотки с элементом Вольта не замыкался, а внутри картон. трубки дв-ся вверх-вниз пост. магнит. При дв-нии маг-та вниз стрелка г-метра откл-сь в одну сторону, при дв-нии маг-та вверх - в др. При изм-нии полюсов маг-та напр-ния откл-я стрелки мен-сь.

Закон эм индукции. (По Фарадею) заряд, переносимый индукц. током ч/з попереч. сеч-е пр-ка, пропорц. кол-ву силовых. линий Ф, пересекаемых пр-ком q = k Ф. (1) Здесь Ф – число сил-х линий, или – маг. поток, k – коэф-т пропорц-ти. Ленц дополнил форм-ку Фарадея правилом:

инд. ток во всех случаях направлен т. о., что его действие противоположно действию причины, вызвавшей этот ток. Максвелл дал совр. ф-ку з-на эм индукции. В СИ формула закона имеет вид: 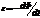(2)

ЭДС индукции возникающая в контуре, пропорц-на скорости измен-я маг. потока, прониз  площадь этого контура.

Формулировка Фарадея получ-ся при вычислении заряда q, протек-го ч/з попереч. сечение замк. пр-ка. Инд. ток в пр-ке i =eçR =-(dФç dt)çR , R– сопр-ние пр-ка. Допустим, в нач. момент t площадку контура пронизывал поток Ф,в конечный момент–поток 0. Для этого достаточно контур повернуть на 90°. dq = idt , то 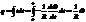Коэф-т k в формуле (1) представляет собой эл. проводимость контура, k = 1çR.

Правило Ленца. Круговой замкн-й контур. n-вектор нормали, направление обхода по правилу прав. Винта (если ввинчивать буравчик по направл тока, то движение рукоятки укажет направление линий магн индукции). Вектор n задаёт направ-е сил. линий B ч/з площ-ку. Допустим, маг. поток Ф ч/з пл-ку увелич-ся. Это значит, что линии B приходят из бескон-ти и сгущ-ся внутри пл-ки. dФçdt > 0 (поток увелич-ся). ЭДС индукции e = - (dФçdt). Знак минус означает, что ЭДС индукции противоположна направл-ю обхода. Инд. ток так же противопол. направл-ю обхода, а сил. линии его маг. поля противопол. линиям внеш. поля B. Потому поле инд. тока ослабляет внеш. поле B, препятствуя его нарас-ю. Т. о., знак “-” в (2) выражает правило Ленца. Если маг. поток Ф ч/з пл-ку контура убывает, сил. линии разбег-ся от центра к бесконечности, то dФçdt < 0, а e = - dФçdt > 0 инд. ток совпадает с напр-ем обхода, его маг. поле усил-т внеш. поле B, препятствуя его убыванию. Величина ЭДС индукции не зависит от материала пр-ка. Она опред-ся исключ-но υ измен-я прониз-го его Ф

Эм индукция и сохранение энергии. Проанализ-ем баланс энергии в явл-ии эм индукции. Для этого рассм. движение пр-ка с током в маг. поле.

Допустим, пр-ник длинной l м скользить в однородном маг. поле по пр-кам, присоед-ным к полюсам ист-ка пост. тока с ЭДС e ₀ Подвижный пр-ник замыкает цепь, её сопр-ние пост-но и равно R , ток в цепи i.Для простоты полагаем, что сам пр-ник и направл-е его движ-я перпенд-ны вектору B. Работа перемещ-я пр-ка под действием силы Ампера F есть 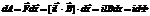.(4)          

Здесь dФ = Bldx = BdS – маг. поток, пересечённый пр-ком при его перемещении на расстояние dx. Т.к. сила Ампера склад-ся из сил Лоренца, не измен-щих энергию движ-я зарядов, то работа перемещ-я пр-ка м соверш-ся не за счёт энергии маг. поля, а за счёт энергии ист-ка тока с ЭДС E ₀. Приняв во внимание тепло Джоуля – Ленца, выдел-еся в пр-ке, полная работа ист-ка тока равна e ₀idt = i²Rdt + idФ.(5) Разделив обе части рав-ва на iRdt и разрешив его отн-но тока i, получаем: 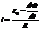(6).Очевидно, - dФçdt – ЭДС индукции. Она напр-на на встречу ЭДС ист-ка тока и ум-ет ток.

Ф-лу (6) получил Гельмгольц Она позв-ет рассма. з-н эм индукции как следствие з-на сохр-я энергии. Чем быстрее скользит пр-ник, тем > линий B он пересекает, тем > ЭДС индукции, тем < ток в цепи. И наоборот. Эта ситуация реализ-ся в якорях эл. двигателей. Чем > нагрузка, тем медленнее вращается якорь, тем < возникающая в нём ЭДС индукции. Поэтому ток, протек-ий по якорю, велик. Велика и потребл-я двиг-ем мощность. С уменьш-ем нагрузки скорость вращения якоря увел-ся, увел-ся так же и ЭДС индукции, ум-щая ток в цепи, и потребл-я двиг-м мощность падает.

Вихревые токи Фуко. Если массивный проводник находится в быстро переменном магн поле, то благодаря его малому электр сопротивлению под действием ЭДС индукции в нём могут возбуждаться большие индукционные токи. Эти токи обнаружил по нагреванию проводников Жан Фуко. Токи Фуко тормозят движение проводников в маг поле. Они возникают в любом случае, когда изменяется магн поток, пронизывающий проводник. В индукционных электропечах тепло индукционных токов используется для плавки металлов. В бытовых микроволновых печах – для приготовления пищи. Выделение же тепла в магнитопроводах нежелательно. С целью его уменьшения сердечники трансформаторов, якоря и статоры электродвигателей набирают из отдельных покрытых оксидным слоем тонких стальных пластин, а на высоких частотах используют сердечники из ферритов с большим удельным сопротивлением.

Самоиндукция. Каждый контур, по к-му идёт ток, создаёт маг поле, а поэтому пронизывается маг потоком собственного поля. Величина этого потока Ф ~току i, протекающему по контуру. Ф = L·i. Коэффициент пропорциональности L н-ют коэффициентом самоиндукции или индуктивностью контура.

При изменении тока в контуре изменяется и пронизывающий его магнитный поток. В результате в контуре наводится ЭДС самоиндукции. .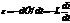

«-» показ-т, что напр-е ЭДС самоиндукции противоположно напр-ю изменения тока. В результате изменение тока в контуре замедляется. Ед индуктивности в СИ. 1 генри (1 Гн) – это индуктивность такого контура, при изменении тока в котором со скоростью 1 А в секунду в контуре наводится ЭДС индукции 1 В.

Энергия м.поля.Если ток в контуре изменяется на величину di, то магнитный поток поля этого тока изменяется на величину dФ = Ldi. Но это изменение потока dФ сопряжено с работой тока dA = idФ.

Если ток увеличивается, то работа тока идёт на увеличение энергии контура с током, так что dA = dW. Отсюда dW = dA = idФ = Lidi. При увеличении тока от 0 до I энергия контура найдётся интегрированием: 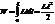.Это энергия магнитного поля, придающая электрическую инертность контуру

Плотность энергии магнитного поля. Для её вычисления рассмотрим секцию бесконечно длинного соленоида длинной l. Полагаем, что на этом отрезке l намотано N витков, магнитная проницаемость сердечника соленоида m, его сечение S Поскольку соленоид бесконечно длинный, то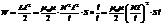        

Разделив на объём Sl, получаем плотность энергии магнитного поля в соленоиде 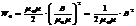.Если в пространстве существуют одновременно электрическое и магнитное поля, то объёмная плотность энергии электромагнитного поля в целом равна сумме энергий электрического и магнитного поля: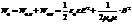

Скин-эффект (поверхностный эффект) — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.Если по проводнику течёт постоянный ток, то его плотность во всех точках сечения проводника примерно одинакова. На каждый заряд действует сила Лоренца, стремящаяся сместить его к центру провода.Рассмотрим механизм скин-эффекта при нарастании и убывании тока. Данное явление используется в важном с промышленной точки зрения методе закалки металлов в промышленности.

а. Ток нарастает. Нарастающая индукция магнитного поля B вызывает появление вихревого эл поля E, к-е у поверхности проводника направлено по току, а на оси проводника – противоположно току. В результате у поверхности ток усиливается, а центре – ослабляется б. Ток убывает. В этом случае ослабевающая индукция B вызывает эл поле E, направленное противоположно первому случаю, то есть на оси – по току, а на поверхности – против тока В обоих случаях вихревое эл. поле на оси проводника препятствует, а на поверхности – способствует изменениям тока. Поэтому на оси проводника переменный ток слабее, на поверхности – сильнее.

Взаимоиндукция (взаимная индукция) — возникновение электродвижущей силы (ЭДС) в одном проводнике вследствие изменения силы тока в другом проводнике или вследствие изменения взаимного расположения проводников. Взаимоиндукция — частный случай более общего явления — электромагнитной индукции.При изменении тока в одном из проводников или при изменении взаимного расположения проводников происходит изменение магнитного потока, созданного током первого проводника и проходящего через контур второго, что по закону электромагнитной индукции вызывает возникн ЭДС во втором проводнике. Если второй проводник замкнут, то под действием ЭДС взаимоиндукции в нём образуется индуцированный ток. И наоборот, изменение тока во второй цепи вызовет появление ЭДС в первой. Направл тока, возникшего при взаимоиндукции, определяется по правилу Ленца. Правило указыв на то, что изменение тока в одной цепи (катушке) встречает противодействие со стороны другой цепи (катушки).

Чем большая часть магнитного поля первой цепи пронизывает вторую цепь, тем сильнее взаимоиндукция между цепями. С количественной стороны явление взаимоиндукции характеризуется взаимной индуктивностью. Для изменения величины индуктивной связи между цепями, катушки делают подвижными. Приборы, служащие для изменения взаимоиндукции между цепями, называются вариометрами связи.

Явление взаимоиндукции широко используется для передачи энергии из одной электрич цепи в другую, для преобразования напряжения с помощью трансформатора.

Трансформатор.Служит для повышения или понижения напряжения переменного тока.его действие основано на явл взаимной индукции. Перем магн поле в первичной обмотке вызывает появление ЭДС взаимной индукции во вторичной обмотке 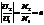коэффициент трансформации. U₂,U₁-абсолют значения напряжений на концах первичных и вторичных обмоток. N₁ и N₂-число витков в первичной и вторичной обмотке. Если число витков во вторичной обмотке больше, чем в первичной-повышающий трансформатор(n<1), наоборот-понижающий(n>1).

Уравнения Максвелла.

 Гипотеза Максвелла о вихревом электрическом поле. Анализируя явление электромагнитной индукции, Максвелл сделал в 60-х. предположение, что причина появления ЭДС индукции состоит в возникновении электрического поля. Это электрическое поле создаётся изменяющимся магнитным полем. При этом проводники играют второстепенную роль. Они являются своеобразными приборами, обнаруживающими это поле. Под действием поля заряды проводимости в проводнике приходят в движение, и если проводник замкнут, в нём возникает индукционный ток.

Электрическое поле, возникающее при электромагнитной индукции, является вихревым. Его силовые линии замкнуты. ЭДС индукции есть 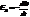,             где Ф – поток магнитной индукции B через площадку S, ограниченную рассматриваемым контуром. В общем случае 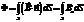Здесь Bn - проекция вектора магнитной индукции B на нормаль n к контуру. С другой стороны, действующая в любом контуре ЭДС может быть представлена как циркуляция вектора электрической напряжённости сторонних сил.

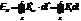Здесь Ест - напряжённость вихревого эл п, Е_l – проекция вектора Ест на касательную к контуру.

Приравняв правые части выражений, получаем количественную связь между напряжённостью вихревого электрического поля и скоростью изменения потока.

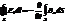.Это ур-е обобщает з-н эл.м. индукции Фарадея. В системе уравнений Максвелла в интегральной форме его обычно записывают вторым.

2. Токи смещения. Гипотеза Максвелла о возникновении вихревого электрического поля, из соображений симметрии, приводит к обратному заключению: всякое изменение электрического поля должно вызывать появление вихревого магнитного поля.

Если включить конденсатор С в цепь, то пока он заряжается, в цепи через лампочку Л будет проходить электрический ток. При изменении переключателем Пк полярности включения конденсатора ток через конденсатор потечёт в обратном направлении до полной перезарядки. Если после каждой перезарядки переключателем Пк менять полярность включения конденсатора, можно заставить лампочку светиться практически непрерывно. Через лампочку течёт пульсирующий ток одного направления, а через конденсатор – ток переменного направления.

    Итак, в отличие от постоянных переменные токи могут существовать и в разомкнутых цепях (в конденсаторе разрыв цепи). В проводниках при этом движутся заряды проводимости, а в пространстве между пластинами конденсатора существует лишь переменное эл. п. Поскольку в этом поле происходит переменная поляризация диэлектрика, то есть переменное смещение связанных зарядов диэлектрика, Максвелл назвал его током смещения. Можно сказать, что ток проводимости в проводнике замыкается током смещения в диэлектрике.

1 уравнение Максвелла в интегральной форме.Согласно Максвеллу, переменное эл. п. в конденсаторе в любой момент времени создаёт такое же м. п., как если бы между обкладками существовал ток проводимости, равный току в проводниках. Иначе, м. п. разомкнутого контура такое же, как если бы контур был замкнут. Это предположение позволяет установить количественную связь между изменяющимся эл.п. и генерируемым им м. п..

Ток в проводнике можно определить как скорость изменения заряда на обкладках конденсатора 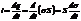где σ – поверхностная плотность зарядов на обкладках площадью S. Разделив на S, получаем плотность тока 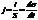.              Если плотность зарядов σ выразить через напряжённость эл. п. в конденсаторе из формулы , σ = εε0Е, и сохранить векторный характер величин j и Е, то получаем плотность тока смещения 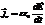.Переменное во времени эл. п. создаёт такое же магнитное поле, как и ток проводимости плотностью .

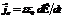В любой т проводника может существовать как ток проводимости, так и ток смещения. Поэтому плотность полного тока jS равна их сумме. 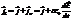.Здесь N – поток вектора электрической напряжённости через площадку S. Интеграл от плотности тока проводимости даёт ток проводимости i через площадку S: .

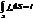После подстановки получаем первое уравнение Максвелла 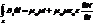. Это ур-е обобщает з-ны Ампера и Био-Савара-Лапласа.

Опыты Роуланда и Эйхенвальда. То, что м. п. возникает вокруг проводника с током ещё не означает, что поле создаётся движущимися эл. зарядами. Не исключалось, что м. п. создаёт проводник, переходящий в некое новое качество, когда в нём существует эл.ток. Поэтому было важно на опыте доказать, что м. п. создаётся любыми эл. зарядами, движущимися в любой среде. Тем самым м. п. токов смещения из гипотезы превращалась бы в реальный факт.

В 1878 г. в лаборатории Гельмгольца американец Генри Роуланд с целью проверки гипотезы Максвелла поставил следующий опыт. Эбонитовый диск толщиной 0,5 см и диаметром 21 см имел на верхней поверхности кольцеобразный носитель электричества – разрезанное в точках а и в кольцо из золочёной фольги. Диск устанавливался на оси и помещался в заземлённую металлическую коробку. Коробка и кольцевой носитель представляли собой конденсатор, ёмкость которого было нетрудно вычислить или измерить. Если к носителю приложить относительно коробки напряжение U, то, зная ёмкость системы, можно всегда определить заряд q на носителе.Над коробкой помещался магнетоскоп М – подвешенная на тонкой нити маленькая магнитная стрелка с зеркальцем, ориентированная в состоянии покоя касательно диску. Когда диск вращался с частотой около ν = 60 об/с, движущийся с кольцевым носителем заряд создавал круговой ток. В результате магнитная стрелка отклонялась, что говорило о появлении м п. Количественная проверка состояла в следующем. Диск останавливался, к точкам а и в носителя подключались проводники, и через кольцевой носитель пропускался такой ток проводимости, при котором магнитная стрелка отклонялась на ту же величину.

Сравнение конвективного тока i = q ν, обусловленного вращением носителя, с током проводимости показало, что токи совпадают.

Опыты Роуланда повторялись с разными результатами и другими исследователями, пока в 1901 – 1904 г.г. русский физик Александр Эйхенвальд окончательно не доказал, что все наблюдаемые в экспериментах токи – проводимости, конвективные и токи смещения – всегда образуют собой замкнутые цепи и генерируют магнитные поля.

   Система ур-й Максвелла в интегральной форме. Всё содержание теории электромагнетизма может быть сконцентрировано в группе математических соотношений, полученных Максвеллом в 60-х годах XIX в. на основе обобщения эмпирических законов электрических и магнитных явлений.

    Полная система у-й, описывающих поля и заряды, включает в себя кроме уравнений поля выражения для сил, действующих на заряды, и законы динамики Ньютона, описывающие движение носителей зарядов под действием этих сил.

  Взаимод полей с материальными средами описывается с помощью макроскопических параметров ε, μ, g, значения которых могут быть в первом приближении вычислены в рамках моделей микроскопической электродинамики. Электромагн явления в области атомных размеров и внутри самих атомов и молекул могут быть описаны только с помощью квантовой электродинамики.

Уравнения М. для с-мы зарядов в вакууме:

Первая и вторая пара ур-й М. в дифференц-ой форме:

 

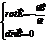
Первая и вторая пара ур-й М. в интегр-ой форме:

 

 

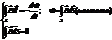
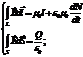
  Q - пространственный заряд. Эти уравнения выражают связь между напряженностью м. п. и эл. п. Полная система ур-й, описывающих поля и заряды, включает в себя кроме уравнений поля выражения для сил, действующих на заряды, и законы динамики Ньютона, описывающие движение носителей зарядов под действием этих сил.

Из 1-го (эм индукция) и 3-го (з-н полного тока (закон Ампера)) диф-х ур-й видна взаимосвязь м-у полями (асимметрия-наличие э.м. волн, т.к. знаки разные), двусторонняя связь полей одно из к-рых с «-» дает возможность сущ-ния эл.м. волн.

  2-з-н отсутствия магнитных зарядов в природе, 4- з-н Кулона в форме теоремы Гаусса.

  В целом, решение этих уравнений довольно затруднительно, так как они зависят еще и от координат, и от времени.

Эл.м. волна представляет собой эл.м. возмущение, распространяющееся в вакууме со скоростью света.

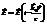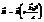Случай плоской волны более простой - это волна , в которой векторы Е и В зависят лишь от времени и одной координаты. 1). ;2). ; где 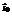-единичный вектор, задающий направление движения фронта волны. Часто используются уравнения волны вида: 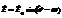; 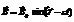, где 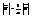; ; 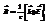 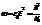или w=2pn - циклическая частота; k=2p/l - волновой вектор. Скорость распространения волны есть величина:  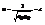, где с - скорость света. Максвелл сделал вывод, что свет и эм волны имеют одну природу, свет-это частный случай эм волны. В однородном диэлектрике 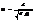-это закон Максвелла. Максвелл ввел особую - полевую форму материи, которая не может существовать в покое и движется со скоростью с. Плоская волна может быть линейно поляризованной, т.е. плоскость колебаний векторов Е и В неизменна во времени. Световое поле - это усреднение квантовой картины взаимодействия фотонов и связанных в атомах электронов.

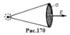
Условия излучения эл.м. волн. Важное практическое значение имеют электронейтральные системы, излучающие электромагнитные волны; системы характеризуются электрическим дипольным моментом 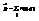и магнитным

дипольным моментом .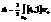

Выделяют два вида излучения:

1.Электр дипольное излучение 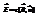, возникает, если р¹0 ;

2.Магнитное дипольное излучение, чья интенсивность на несколько порядков меньше электрического дипольного излучения (возникает, если ¹ 0).

 Шкала эл.м. волн: радиоволны - 10⁵-10¹² м, инфракрасные - 8×10^-7-10^{-9 м,видимыйсвет-(ф)4*10-7}-(к)8*10^-7м, ультрафиолетовый-1*10^-8-4*10^-7м, рентгеновские лучи - 10^-14-10^{-8 м (проходят через вещество), гамма-излучение-}l 10^-10м (корпускулярные свойства).

Энергия и импульс э/м поля.

Перенос энергии и импульса в ЭМ-волне. Эл.м.волны переносят в пространстве энергию.

В случае упругих волн эта энергия слагается из потенциальной энергии деформации среды и кинетической энергии движения её частиц. Энергия же электромагнитных волн слагается в любой момент времени из энергии взаимосвязанных электрического и магнитного полей.

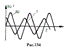
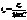Энергия, переносимая электромагнитными волнами определяется вектором плотности потока энергии S, то есть количеством энергии, которое переносится волновым процессом через единичную площадку σ, ориентированную перпендикулярно вектору скорости движения волнового фронта v в данный момент времени . Здесь w₀ – плотность энергии ЭМ-поля. Так как ;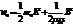

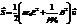
Вектор S можно представить через характеристики ЭМ-поля E и B. Как и в колебательном контуре средние энергии электрического и магнитного полей в ЭМ-волне одинаковы. Е и В изменяются в одной фазе, то одинаковы и мгновенные значения плотности энергии, то есть εε₀E² = B²çμμ₀ в итоге можно записать: 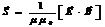.Вектор Пойнтинга

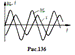Электромагнитное поле массой и импульсом. Из формулы Эйнштейна W = mc² = w₀V, где V – объём, получаем пространственную плотность распределения массы поля: 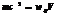Þ .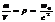

Импульс единичного объёма электромагнитной волны есть .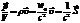

Пон-е эн-гии в физике соот-ся с пон-ем работы (эн. рассм-ся как запасы работы, кот. м.б. совер-на).

-

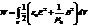энергия э/м поля в заданном объеме.

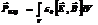-импульс э/м поля.

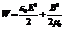-объемная плотность энергии поля.

 

 

28.Перем. эл. ток

Получение гармонич. тока технич. частоты. Перем наз-ся ток электр зарядов, величина и направление к-го изменяются во времени. З-н измен-я тока м. б. каким угодно. Но в практике наиболее важны гармонич. токи, их величина измен-ся во времени по з-ну sin или cosin. Если частота изменений тока не превышает нескольких сотен герц, её называют технической (промышленной). Перем. токи промыш. частоты исп-ются в кач-ве носителей энергии. Если S – пл-дь контура, а n - его единичная нормаль, то маг. поток, прониз-щий контур, есть 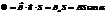  Если контур

покоится, то Ф=const, и ЭДС инд-ии в контуре нет. При вращении жёсткого контура (S = const) в однород. маг. поле (B=const) в нём наводится ЭДС индукции

  

 

технически удобнее реализовать равномер. вращ-е контура, когда a=wt, где w-угл. скорость вращения. Отсюда daçdt=w и ε=BSwsinw=ε_asinwt (3) Здесь ε_a = BSw - амплитуда ЭДС. (4) Если контур замкнут на некот. сопр-ние R, то под действием переем. ЭДС в контуре возникает переем. ток той же частоты, колебания кот. совпадают по фазе с колебаниями ЭДС

 

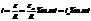
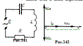Здесь 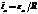 - амплитудный ток.

Частота колебаний тока n = w / 2p,, период Т = 1çn = 2pçw.

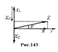Цепь с актив. сопр-ем R, L=0 и С=0. Пусть в цепи действует внеш. синусоид. ЭДС e = e_а Sinwt В случае квазистац. тока в люб. мом-т времени дл

 контура справ-во 2-е пр-ло Кирхгофа i R = e_a Sinwt,Þ .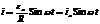

Ток ч/з актив R совпадает по фазе с ЭДС. Т. к. напряжение на сопр-нии равно ЭДС, то мож. сказать, что измен тока и напряжения на актив. R совпад по фазе.

Цепь с конд-ром,(С-емкость) 2-е пр-ло Кирхгофа запишется так: i R + u_c = e.. Но R = 0, u_c = e (u_C – напряжение на обкладках конд-ра. Т. к. u_C= qçC, где q – заряд на обкладках конд-ра, то получаем: 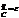, или q = e_a C×Sinwt

Продиф-вав по времени получаем ток в цепи

с ёмкостью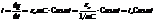

Выражение есть амплитудный ток.

 

 

1çwС = X_C - сопр-ние конд-ра переем. току – ёмкостное сопр-ние. Т. к. coswt = sin(wt + pç2), то, сравнив напряж-е на конд-ре u_c = e = e_a Sinwt t с током i = i_asin(wt + pç2), видим, что ток в цепи опережает напряж-е на конд-рена 1/4 периода Если сместить начало координат на pç2 влево, для чего из аргументов ф-ции вычесть pç2, то выраж-я для тока и напряж-я приним. вид:

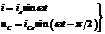
Цепь с катушкой, R=0,. В контуре дейст-ют две ЭДС: внеш. гармонич. e = e_a Sinwt и ЭДС индукции, противодейст-щая направлению изм-ния внеш.. По 2-му пр-лу Кирхгофа их сумма в люб. мом-т времени=0 т к R=0

 

Чтобы выразить зависи i(t), разделяем переменные и интегрируем

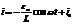
Пост. интегрир-ния i₀

 отбрас-ем, т. к. это составляющая пост. тока ч/з катушку и в данном исслед-нии не интересна.,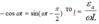

Sin(wt - p/2) = i_a Sin(wt - p/2). Величина wL = X_L им. смысл индуктив. сопр-ния цепи. Напряж-е на зажимах катушки совп-ет с внеш. ЭДС. u_L = e_a Sinwt = u_La Sinwt Поэт. ток в цепи с L отстаёт от напряж-я на L сопр-нии на 1/4 периода. Если сместить на графике начало корд-т на pç2, то выражения для тока и напряж-я на индукт-ти приним-т вид:

    

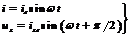
З-н Ома в цепи переем. тока. Рассм. цепь, включающую в себя R, C и L. Если ток квазистац-ый, то в люб. мом-т времени его величина одинакова во всех точках цепи и равна i = i_acoswt. U на каж. эл-те цепи соотв-но равно u_R = i_aRcoswt, u_C = i_aX_Ccos(wt - pç2), u_L = i_aX_Lcos(wt + pç2). Как пр-ло, диаг-мы изобр-ся в тот мом-т времени, когда i = i_a). Каж. вектор амплитуд. напряж-я м представить как произведение действит-го числа i_a на векторы R, X_C, X_L, Поэтому для вычисления полного сопр-ния цепи нужно найти векторную сумму сопр-ний всех эл-тов цепи, соединённых послед-но. Модуль полного сопр-ния Z равен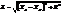

 

|X_L - X_C| - реактив. сопр-ние. Умножив диагр-му сопр-ний на скаляр. величину амплитуд. тока i_a, получаем диагр-му напряж-ий .Угол j определяет сдвиг по фазе м/у I в цепи i и прилож. к ней U u. М/у величинами амплитуд. тока i_a и амплитуд. напряж-я u_a сущ-ет пост. связь. 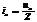 Разделив это выр-ние на 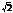, получаем  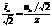Но -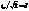 

эфф. ток. Если ввести по формальной аналогии

понятие эффект. напряж-я 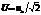,то

получаем: 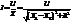З-н Ома для цепи 

переем. тока. Эфф I протекающий по участку цепи, пропорц. эфф. U, приложенному к этому участку, и обратно пропорц. полному R цепи.

Дейст. и ср. значение перем. тока. для хар-ки перем. тока во мн. случаях удобнее указывать величину пост. тока, производящего такое же действие, как и данный переем-ый. В кач-ве такого действия принято брать тепловой эффект. соотношение м-у эффект. (действующим) и амплит. токами. За один период Т перем. Ток

 выделяет тепло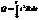

Но такое же кол-во тепла за время Т выд-т пост. ток некот. величины I. Так что

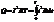Þ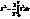

Подставив сюда i = i_asinwt  получаем 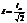 - эфф. знач-е тока . Пост. ток i_ср переносит за 1/2 периода такой же заряд q, как и данный переем  Отсюда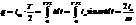  

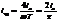
Матем-ски эфф ток есть среднекв-ный, а ср. ток–среднеариф-ий по модулю. Выразив из получ-х ф-л амплит. ток i_a, найдём связь м/у эфф. и ср. токами.

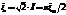Þ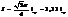

Квазистационарные токи – это такие перем токи, при к-х мгновенные значения I практически одинаковы во всех точках цепи. Т.к. распространение элек и магн полей в пространстве происходит с конечной скоростью, то для того, чтобы в самых отдалённых участках цепи “почувствовалось” изменение ЭДС, д пройти некоторое время t. Если ЭДС изменяется очень быстро, то напряжённость электр поля в удалённых точках цепи не успевает за изменением ЭДС.

Если l – линейный размер контура, с – скорость распространения в контуре эм волны, то t = lçc. Время полного изменения ЭДС равно периоду Т. Если период Т много больше времени t, то ток является квазистационарным.

Т >> lçc, или Tc >> l, или длина цепи l << λдлины эм волны, соответствующей переменному току. Критическое значение частоты n в цепи n_max = сçl. Выражения формул через синус и косинус. Часто I и U удобно выражать ч.з ф-ю cos. Фазовый сдвиг м/у I и U на элементах цепи остаётся прежним, а сам переход от ф-и синуса к ф-и косинуса графически соответствует переносу начала координат по оси аргументов на pç2 вправо.

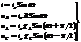
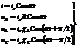
Здесь X_L = w L, X_C = 1çwС.

Мощность в цепи переменного тока. Мгновенное значение мощности в цепи переменного тока есть p = iu , где i и u – мгновенные I и U

Пусть между I и U есть сдвиг по фазе на угол j.

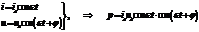Среднее значение мощности переменного тока за период T найдётся интегрированием. 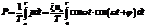. Т.к. cos(wt + j) = coswt cosj - sinwt sinj, а cos²wt = (1+cos2wt)ç2 .

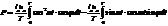Cosj и sinj - const данной цепи числа и выносятся из под интеграла. Правый интеграл обращается в нуль, а левый от cos²wt распадается на два .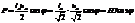

Здесь I и U – эффективные ток и напряжение.

Величина cosj называется коэффициентом мощности. Чем > косинус фи, тем < бесполезные потери в цепи переменного тока.

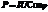 определяет активную мощность, к-я х-ет скорость необратимого превращения электр энергии в другие виды энергии.

Произведения эффективных I и U н-ют полной мощностью и обозначают S.

I×U = S, P = S×cosj.

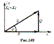Q = IUsinj = S×sinj - реактивная мощность. Она х-ет скорость передачи энергии от источника тока к приёмнику и обратно.

Величины P, S, Q образуют в комплексной плоскости треугольник мощностей для цепи с преобладанием индуктивности.

Ед активной мощности P – ватт (Вт), ед полной мощности S – вольт-ампер (В×А), ед реактивной мощности Q – вольт-ампер-реактивный (вар).

Реактивная мощность, потребляемая в электрических цепях, вызывает дополн активные потери в подводящих проводах. Для устранения перегрузок и повышения коэффициента мощности делают компенсацию реактивных нагрузок, максимально приближая X_L к X_C. Амперметры и вольтметры в цепях переменного тока проградуированы на эффективные I и U. Поэтому произведение показаний амперметра и вольтметра, подключённых к нагрузке, даёт полную мощность S, потребляемую данной нагрузкой. Для измерения активной мощности применяются специально сконструированные ваттметры

 

  

29. Эл. колебания в колеб. контуре.

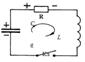Колеб. контур - цепь, содержащая С и L. Реальный контур всегда имеет некот.активн (омическое) R.

Свобод. (незатух.) колебания в контуре В идеал. контуре, в кот. отсутствует затухание, R = 0, колебания должны продолжаться бесконечно долго. При этом макс. энергия конд-ра 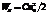, а макс. энергия поля катушки составляет 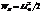. Когда конд-р макс-но заряжен, i = 0, 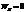, вся энергия колебаний заключена в эл. поле. Когда конд-р разряжен, u = 0, а ток максимален вся энергия контура заключена в маг. поле катушки. Ср. и макс. энергии эл. и маг. полей одинаковы, 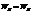. Однако колебания в люб. реал. контуре даже из сверхпроводящих материалов обязательно затухают. Это происходит потому, что контур с перем. током излучает электромаг. волны, кот. уносят запасённую в нём энергию. В дифф-ном ур-нии эти потери не учтены.

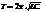- ф-ла Томсона.

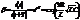декремент затухания

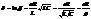- логарифм-ий декремент затухания

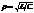- волновое сопр-ние

Затух. колебания Если на пластинах конденсатора есть заряд q, то при замыкании ключа в цепи возникает изменяющийся во времени ток. Для его определения составим дифф. ур-ние, описывающее изменение заряда на обкладках конд-ра. В случае квазистац. тока для контура справедливо 2-ое пр-ло Кирхгофа: iR=UC+e. Здесь i=dq/dt, , Отсюда: 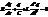,или  Это дифф. ур-ние затух. колебаний. Его решение зависит от соотношения между коэф-тами. Обозначив R/L=2n, 1/CL=w₀², получаем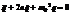

а). Периодич. затух. колебания. Если w>>n, то решение имеет вид:

q = q₀ e-nt coswt,

i = q₀ w e-ntcos(wt + p/2),

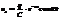.Здесь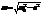

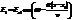б). При n>w разряд конд-ра апериодический, а w и Т мнимые числа. Если n>>w, заряд на конд-ре при разряде и заряде изменяется по экспоненц. з-ну. При разряде: 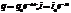. При зарядке: 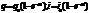. Здесь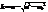

Из равенства n=w0 находим критическое сопр-ние контура. При R<<Rкрит в контуре возникают периодические колебания, при R>Rкрит-апериодические.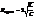

2).Вынужденные колебания. Если в контуре действует периодич. ЭДС e=eаcosWt, то уравнение колеб. электр. заряда на обкладках конденсатора принимает вид: 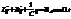Решение этого ур-ния состоит из 2-х членов, и при n<<w0 имеет вид:

.

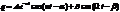Первый член описывает собст. затух. колебания в контуре. Спустя время t>>t(t-время релаксации колеб.) эти колебания практически исчезают. Остается лишь 2-я часть описывающая вынужденные колебания: q|t>>t=Bcos(Wt-b), В- амплитуда вынужд. колебаний. 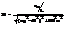; ; 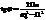Дифф-я по времени, получаем ток в контуре. i = = - BWSin(Wt - j) = BWCos(Wt - j + p/2). Величина ВW= iа есть амплитудный ток. Он зависит от соотношения частот w0 и W.

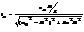
Если частота изменения внеш. ЭДС W приближается к собст. частоте своб. колебаний в контуре w0, то ток возрастает до некоторого макс. значения, называемого резонансным. При W®w0 последняя формула примет вид: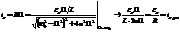

 

Очевидно, резонансная частота 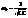, а резонансный ток iа=eа/R. Рассмотренная ситуация соответствует резонансу напряжений (последов. резонансу) в цепи переем. тока, а ф-ла амплитуд. тока соответствует з-ну Ома для цепи переем. тока. Т.к. 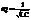, n=R/2L, то  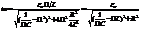  Чем больше добротность контура, тем уже его резонансная кривая, тем выше его избирательность (селективность). Поэтому с увеличением добротности Q ширина частот ±(W-w0), при которых в контуре раскачиваются значительные токи, становятся уже. Этот интервал частот, близких к w0, называется полосой пропускания контура.

Искровой колебательный контур.

Для возбуждения в колебательном контуре незатух. колебаний выс. частоты использ-ся Искровой колебательный контур, которой изобрёл в Герц. После включения ист-ка пост. напряжения конд-р ч/з дроссельные катушки заряжается, и напряжение м/у его обкладками увелич-ся. Когда оно достигает значения напряжения пробоя, через разрядник проскакивает искра, замыкающая колеб. контур, и в контуре возникает цуг затух-х колебаний. Он обрывается, когда напряжение на искровом разряднике упадёт до напряжения гашения искры.

Искровой колебательный контур представляет собой автоколебательную систему. Один из главных недостатков его в том, что энергия вводится слишком редко– м/у цугами. Поэтому трудно обеспечить стабильность амплитуды ВЧ колебаний

Генератор ВЧ колебаний на ламп. триоде.

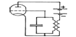
Вследствие тепловых флуктуаций электронов контуре C–L1 самопроизв возникают слабые колебания. Но изменение напряжения на обкладках конденсатора С вызывает изменение потенциала сетки S триода. При полож-ном потенциале верхней пластины конд-ра триод открывается, в анодной цепи течёт ток, кот. ч/з индуктивную связь м/у катушками L1 и L2 усиливает ток в контуре. Когда конд-р перезарядится в обратном направлении, лампа заперта, ч/з катушку L2 тока нет. Затем весь процесс повторяется. Т. о., ток в анодной цепи течёт лишь в те мом-ты времени, когда лампа открыта, и когда маг. поле катушки L2 подпитывает ток в контуре. Управление электронной лампой с помощью цепи обратной связи может осущ-ся разными способами. Наряду с рассмотренной индуктивной связью часто применяется также ёмкостная и автотрансформаторная обратная связь.

Токи высокой частоты, ТВЧ. С помощью генераторов эл. колебаний можно вырабатывать почти синусоидальные перем. токи частотой в тысячи и миллионы герц. Благодаря вытеснению быстроперем. токов к периферии пр-ка вследствие скин-эффекта, оказывается возможным с помощью ТВЧ закаливать поверхность стальных деталей, не уменьшая их пластичности в глубине. Использ токов частотой в сотни и тысячи герц эффективно при индукционном нагреве металлов в плавильных индукционных электропечах, поскольку вихревые токи Фуко увеличиваются с ростом частоты электромаг. поля.

ТВЧ широко используются при высокочастотной сварке и в многоканальной телефонной связи.

 

Интерференция световых волн

Сложение световых волн. Пусть на оси ОХ находятся два источника S1 и S2 в точках с координатами х1 и х2 В момент времени t = 0 ист-ки начали излучать две монохроматич. одинак. частоты w линейно поляризов-е в 1й плоскости световые волны. Здесь v – ск-ть распр. Волны.

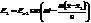Суперпозиция: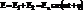

Здесь j = w(х2 – х1)/v - сдвиг фаз м/у волнами, расст-е м/у источниками D = х2 – х1.Сдвиг фаз определяет амплитуду Еа суммарной волны . Если разность фаз в данной точке пр-ва постоянна, то амплитуда результир. колебания в этой точке постоянна. Усиление интенсивности света (j = 0, Еа = Еа1 + Еа2), или ослабление (j = p, Еа = Еа1 – Еа2). При равенстве амплитуд Еа1 = Еа2 и при j = p,  Еа = Еа1 – Еа2 = 0. Происходит полное гашение света.

4.Интерференционная картина. В реальных случаях складываемые волны сходятся обычно под некотор. углом друг к другу. В разных точках пр-ва j оказ-ся разной. Возникает пространственное распределение интенсивности света в виде чередующихся светлых и темных полос -интерференционная картина. Явление сложения волн с одинаковой частотой и постоянной во времени, достаточном для наблюдения, разностью фаз, при котором происходит перераспределение интенсивности в пространстве, называется интерференцией. Интерференционная картина наиболее контрастна, когда амплитуды складываемых волн одинаковы.

5.Когерентность – согласованность во времени нескольких колебательных или волновых процессов, проявляющаяся при их сложении. Получение когерентных лучей от естеств. Источ-ов возможно путем расщеплен. луча от одного ист-ка и создания м-у ними постоянного сдвига фаз. В этом случае лучи повторяют себя во всех деталях и потому могут интерферир-ть м-у собой. Фаза колебан. вектора Е на его протяжении непрерывно изменяется. Поэтому «голова» цуга не когерентна его «хвосту». Время t, в течен. кот. фаза колебаний в световой волне, измер-ая в постоянной точке пр-ва, изменяется на p, наз-ся временем когерентности. Расстояние сt, с - длина когерентности. Свет разных источников имеет длину когерентности от нескольких микрометров до нескольких километров. В пл-ти, перпенд-й направлен. ее распростр-я, применяют термин пространственная когерентность. Она опред-ся площадью круга диаметром l, во всех точках которого разность фаз не превышает величины p. Пр-во когер-ти у точечн. Ист-ка естеств. света приближ-ся к объему усеченного конуса длинной неск-ко мкм и диаметром основания неск-ко мм. С удалением от источника оно увеличивается.

Практич. методы наблюден. Интерференции: Опыт Юнга.

             

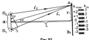
Даёт на экране интерфер. картину в виде системы парал-х щелям полос. Удобен для теоретического изучения 2х лучевой интерф. с целью получения количественных оценок. S1 и S2 – когер-е ист-ки света, излуч-е в одинаков. фазе, то в любую произвольн. точку А экрана Э3 будут приходить волны с разностью хода D = l2 – l1. рисунке а<<L и D/а = yçL получ-м велич. разности хода, D = аyçL. , k = 0, 1, 2, 3, (max), 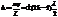, k = 1, 2, 3,(min), k – номер полосы.

 

Бизеркала Френеля.

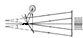
Свет от источника, заключенного в светонепроницаемый кожух, через отверстие в нем попадает расходящимся пучком на два плоских зеркала. Угол между зеркалами a » 179°. Достоинство – хорошая освещ-ть, недостаток – сложность юстировки зеркал на оптической скамье.

 

Бипризма Френеля

Достоинства – хорош.освещ-ть и простота юстировки, недостаток – требуется специальная бипризма, изделие оптической промышленности.

Билинза Бийе,

Собирающая или рассеивающая линза разрез-ся по диаметру, и обе половины слегка раздвигаются в стороны. Чем дальше раздвинуты друг от друга полулинзы, тем сильнее сжата интерф.картина, тем уже полосы.

Зеркало Ллойда, Прямой пучок от источника S интерферирует с пучком, отраженным от зеркала.

7.Интерференция в тонких пленках. 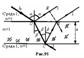Пусть на пов-ть прозрачной плоскопараллельной пластинки в точку О падает луч света Часть эн-ии падающ. луча отраж-ся в точке падения (луч 1), часть проходит в пластину и, отразившись от ее грани, выходит в точке В (луч 2). Часть эн-ии проходит сквозь пластину (луч 3) и часть поглощается. Рассмотрим лучи 1 и 2, отразившиеся от пластинки в точках О и В. Лучи 1 и 2 парал-ны, когерентны и мало отличаются по интенсивности. Вычислим разность хода лучей 1 и 2. При отражении от оптически более плотной среды свет теряет полволны, то есть луч как бы проходит дополнительный путь lç2. В результате полная разность хода D между лучами 1 и 2 равна:  Преобразовав выражение запишем условия максимума и минимума. 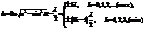Число k порядок интерфер. max (min).

Число k называется здесь порядком интерференционного максимума (минимума). Оно тем больше, чем толще пластина.

Если смотреть на тонкую освещенную пленку, то при разности хода D, не выходящей за пределы длины когерентности света, можно увидеть на ее поверхности темные и светлые полосы. Различают полосы равной толщины и полосы равного наклона.

8.Просветление оптики. Если на поверхность стеклянной пластинки с показателем преломления n2 нанести тонкую пленку с показателем преломления n < n2, то, подобрав толщину пленки а так, чтобы в отраженных лучах наблюдался интерференционный минимум, получаем оптическую систему с увеличенным коэффициентом пропускания. Наиболее полное гашение происходит при 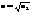. Просветление рассчитывается обычно для желто-зеленой области спектра.

Двухлучевые интерферометры. Это измерит. приборы, в кот. исп-ся интерфер. двух световых волн.

а. Интерферометр Ж. Жамена,

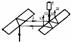 Сост-т из двух толстых плоскопараллельных пластинок высокооднородного стекла, смонтированных на массивной плите почти параллельно друг другу. Лучи 12 и 21 налагаются друг на друга и интерферируют между собой. Интерференционная картина наблюдается в зрительную трубу Т, сфокусированную на бесконечность. Исп-ся для измерен. показателей преломлен. газов, жидкостей, для измерения концентрации растворов.

б. Интерферометр Дж. Релея.

Взаимод-ие пучки выдел-ся с пом-ю д2х щелевых диафрагм. Пройдя кюветы пучки собир-ся в фокальной пл-ти линзы, где обр-ся интерфер.картина полос равн. наклона, рассматрив-я ч-з окуляр. Измер-т показат. преломлен. газов.

в. Интерферометр А. Майкельсона,

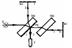1881 г. Сконструированный с целью определения влияния движения Земли на скорость света, он сыграл выдающуюся роль в истории науки. Прибор построен на основе двух плоских зеркал и двух стеклянных пластинок (рис.100).

Луч света от источника S падает на полупрозрачную пластинку Пл1, покрытую тонким слоем серебра или алюминия. В точке О луч расщепляется. Луч 1 сквозь прозрачную пластинку Пл2 идет на неподвижное зеркало Зк1. Отразившись от него в точке В, он возвращается к пластине Пл1 и, отразившись от нее в точке О, попадает в зрительную трубу Т.

Луч 2 идет на зеркало Зк2 и, отразившись от него в точке С, через пластину Пл1 также попадает в трубу Т.

Луч 2 дважды проходит сквозь пластину Пл1. Чтобы скомпенсировать возникающую за счет этого дополнительную разность хода, на пути луча 1 помещается точно такая же пластинка Пл2.

 Если плечи интерферометра одинаковы, то лучи 1 и 2 имеют одинаковую интенсивность, когерентны и приходят в зрительную трубу с нулевой разностью хода. При перемещении одного из зеркал, например, интерфер. полосы перемещ-ся. Поэтому, измеряя смещение полос, можно с очень высокой точностью измерить отрезки длин.

 

 

31 Дифракция света – явление, состоящее в загибании световых волн в обл. геомет-ой тени.

Принцип Гюгенса -Френеля. Свет есть процесс распространения в пр-ве генерируемых ист-ком электромаг. волн. Каж. точка фронта волны есть ист-к вторичных волн. Вторичные волны когерентны и поэтому интерферируют м/у собой.

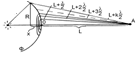
Зоны Френеля а)Объяснение прямолинейного распространения света. Волновой фронт Ф в однородной изотопной среде имеет в произвольный момент времени форму сферы радиуса а. Почему наблюдатель, находящийся вне волнового фронта в точке А, не воспринимает всю сферу как светящуюся поверхность? Ведь в точку А должны приходить все вторичные волны от всех видимых точек сферы. Для подсчета суммарного действия вторичных волн в произвольной точке А Френель предложил разбивать волновой фронт на кольцевые зоны.Граница первой зоны очерчивается лучом из точки А длиной L + λç2, внеш. граница второй зоны –L + 2λç2, третьей зоны –L + 3λç2 и так далее. Внеш. граница произвольной k-той зоны очерчивается лучом L + kλç2. Шаровой сегмент высотой х и радиусом R, содержащий k зон имеет площадь 2pах, где а – радиус сферы. Величина х найдется из условия . Пренебрегая малыми членами l2 и х2, получаем 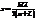. Отсюда площадь k зон 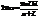. Интенсивность I электромагнитной волны пропорциональна квадрату амплитуды вектора напряженности Е0 электрического поля волны, I ~ Е02. Поэтому подсчет суммарной интенсивности сводится к сложению амплитудных векторов Е01, Е02, Е03 и так далее. Нечетные векторы направлены в одну сторону; а четные – в противоположную, поскольку волны от зон в точке А сдвинуты по фазе одна от другой на lç2. Это вытекает из условия построения зон.

С увеличением номера зоны проекция площади зоны, видимая из точки А, постепенно уменьшается. Уменьшается в точке А и модуль вектора Е0. Поэтому Френель предложил записать сумму так: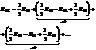  

При постепенном убывании Е0 суммы в скобках стремятся к нулю. Поэтому .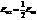

Действие всей волны в точке А сводится к половине действия центральной зоны. Вторичные волны от других участков волнового фронта, интерферируя, гасят друг друга. Радиус центральной зоны 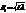 очень мал.

Распространение света от S к А происходит так, как если бы световой поток шел внутри очень узкого прямого канала вдоль оси SA. Этот вывод и есть объяснение прямолинейного распространения света в волновой теории.

Дифракция на круглом отверстии. Пусть в непрозрачной стенке есть круглое отверстие радиуса R. На оси отверстия слева находится точеч. ист-к S, излучающий монохром. свет с длиной волны l Часть световых волн проходит сквозь отверстие и распростр-ся вдоль оси ОХ. 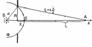Что должно наблюдаться – свет или темнота в точке А, расположенной на оси отверстия в сторону от источника S. Для ответа на этот вопрос достаточно определить, четное или нечетное число зон укладывается на фронте волны Ф в пределах отверстия. При чет. числе зон в точке А – темнота, при нечет. – свет.

Для изучения дифракции на одномерных препятствиях, таких как прямолинейный край полубесконечного экрана, щель и цилиндр, Артур Шустер предложил разбивать плоский волновой фронт не на кольцевые, а на полосатые зоны Френеля. (зоны Шустера)

Дифракция на краю прямолинейного полубесконечного экрана. 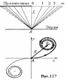 Участки правой спирали Корню соответствуют действию зон, расположенных слева от точки О.

Совмещаем плоский волновой фронт с плоскостью экрана и производим разбиение фронта на зоны Шустера (прямые полосы перепендик плоскости рисунка), параллельные краю экрана.Если точка А находится точно под краем препятствия, то все левые зоны Френеля оказываются закрыты препятствием. Отсюда длина светового вектора Е в точке А равна половине длины вектора Е¥ от бесконечного волнового фронта. .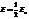

При смещении точки А вправо открывается столько полувитков левой спирали, сколько укладывается левых зон. При смещении точки А влево в область геометрической тени закрываются и часть полувитков правой спирали Вычисленный так вектор Е позволяет найти распределение интенсивностей в дифракционной картине на краю полубесконечного экрана

дифракция Фраунгофера. Йозеф Фраунгофер изучил в 1820 г. типы дифракции в параллельных лучах. Дифракционная картина, образованная параллельными лучами, формируется в идеале на бесконечности от препятствия, а реально в фокусе собирающей линзы. В результате освещенность картины сильно увеличивается.

В отличие от дифракции в сходящихся лучах, называемой дифракцией Френеля, дифракцию в параллельных лучах называют дифракцией Фраунгофера. Последняя имеет важное значение в виду того, что на ее основе создан такой замечательный многолучевой интерферометр как дифракционная решетка.

 

Дифракция света на щели. 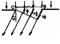 Пусть на щель шириной а перпендикулярно падает пучок параллельных лучей Щель СВ вырезает часть падающей плоской волны. Все точки этой части фронта являются источниками вторичных когерентных волн, которые интерферируют друг с другом. Результат интерференции в любом направлении под углом j можно определить, если разбить щель на зоны так, чтобы каждые две вторичные волны были сдвинуты друг относительно друга на полволны, то есть lç2.

Если разбиение дает четное число зон, то все волны попарно гасят друг друга, и в направлении j наблюдается минимум освещенности. Если же разбиение дает нечетное число зон, то одна волна остается не скомпенсированной, и в направлении j наблюдается максимум освещенности.

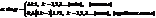 4. Дифракционная решетка – это система из большого числа параллельных щелей одинаковой ширины а, расположенных на одинаковом расстоянии друг от друга b. 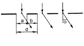Рас-ние a + b = d называется периодом решеткм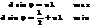

dsinφ = ± kλ, k = 0, 1, 2, 3 (главные максимумы         решётки)(N∙d)sinφ = ± kλ, 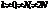(вторичные мин с-мы N щелей)Способность решетки разлагать белый свет в спектр позволяет использовать ее как спектральный прибор. Основными хар-ками дифракционной решетки как спектрального прибора являются дисперсия и разрешающая способность.

 

 

32. Поляризация световых волн.

Поляри-я– это одно из фундам-х св-в ЭМ излучения. Оно состоит в неравноправности различных направлений в плоскости, перпен-ой световому лучу. Поляр-я присуща т-ко поперечным волнам. Поперечность световых волн выражается в том, что колеблющиеся в них векторы напряженности электрического поля Е и индукции магнитного поля перпендикулярны направлению распространения волны. Ест-ный свет, не поляризован. Хотя каждый элементарный цуг, излучаемый атомом, поляризован, плоскости поляризации разных цугов (плоскости колебаний Е) хаотично ориентированы в простр-ве. Для того, чтобы получить пучок света, плоскости поляризации цугов в котором совпадают в оптике используются два способа: взаимодействие световых волн с границей раздела сред и взаимодействие света с анизотропной средой – кристаллом. Рассм-м 1-й способ, основанный на взаимодействии электр-ой волны с границей раздела сред. Это взаим-ие зависит от того, как расположена относительно плоскости падения плоскость колебаний вектора E волны. Выделим и рассмотрим здесь два случая:

а. Плоскость колебаний вектора E лежит в плоскости падения; б. Плоскость колебаний вектора E лежит перпендикулярно плоскости падения.

Коэфф-ты отраж-я и пропуск-я по интенсивности. При падении на границу раздела двух сред неполяризованного света его интенсив-ность I может быть представлена как сумма интенсивностей двух его компонент, 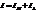. Здесь 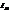- интенсивность компоненты, вектор  которой колеблется в плоскости падения, - интенсивность компоненты, вектор  которой перпендикулярен плоскости падения. В силу случайной ориентации плоскостей колебании 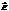 отдельных цугов обе этих компоненты равноправны,  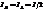Отсюда можно найти суммарный коэффициент отражения по интенсивности неполяризованной волны, падающей на границу раздела сред.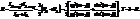

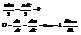
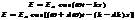
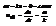Закон Брюстера. Если β+α = 90°, то tg(β+α )= ∞, а 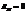. Следовательно, если луч естественного света падает на границу раздела сред под углом α = 90°– β, то в отражен-ном луче будут присутствовать только те волны, вектор  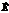которых перпендикулярен плоскости падения и отражаться будет полностью поляризованная волна. Угол полной поляризации из закона преломления.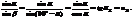

Угол падения, при котором отраженный от диэлектрика свет полностью поляризован, открыл эксп-но в 1815 году Д. Брюстер. 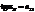 - з-н Брюстера,α Б– угол Брюстера.

Поляризаторы – это устройства, позволяющие выделить из пучка естественного света поляризованную в одной плоскости компоненту.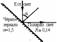

Двойное лучепреломление. Бартолин открыл явление двойного лучепреломления. Суть его в том, что пучок естественного света, падая перпендикулярно на грань кристалла исландского шпата расщепляется на два пучка. Один из них продолжается без преломления, как в изотропной среде, другой же отклоняется в сторону, нарушая обычный закон преломления. Не отклоняющийся луч 1 назвали обыкновенным, а отклоняющийся луч 2 – назвали необыкновенным. В исландском шпате существует одно направление, вдоль которого нет двойного лучепреломления. Это направление называют оптической осью кристалла. Если на кристалл падает естественный свет, то интенсивности обыкновенного и необыкновенного лучей одинаковы. Основная их особенность в том, что оба этих луча линейно поляризованы, причем векторы  колеблются во взаимно перпендикулярных направлениях. Если передняя и задняя границы кристалла параллельны между собой, то оба луча на выходе из кристалла параллельны друг другу. Кроме ориентации плоскости колебаний вектора  оба луча вне кристалла ничем не отличаются друг от друга.

Закон Малюса. Чтобы убедится в том, что свет поляризован, нужно на его пути поставить второй поляризатор, называемый в этом качестве анализатором. В 1810 году Этьен Малюс нашел закон изменения интенсивности линейно поляризованного света после его прохождения через анализатор. 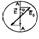I = I0cos2j Здесь I0 - интенсивность линейно поляризованного света, падающего на анализатор, j – угол между плоскостью поляризации света, падающего на анализатор, и плоскостью пропускания анализатора. Закон Малюса вытекает из того, что через анализатор проходит составляющая вектора E0 падающей волны, приходящейся на плоскость пропускания анализатора АА Очевидно, E = E0cosj. Но интенсивность света пропорциональна квадрату амплитуды вектора E. Следовательно: I0 = kE02, I = kE2 = kE02cos2j = I0cos2j. Здесь k – коэффициент пропорциональности.

 

 

33.Распространение света в среде.Дисперсия света- это завис-ть показателя преломлен вещ-ва от длины волны света. Первым изучать дисперсию стал Ньютон. Пропустив узкий пучок солнеч света, ч/р стеклянную призму,он получил на экране окрашенное пятно,кот назвал спектр.Ньютон объяснил появление спектра тем, что лучи разного цвета по-разному преломляются.В рез-те пучок белого света расщепляется на семь цветов.Более всего отк

лоняются фиолетовые лучи,менее всего-красные. Дисперсия света сводится к завис-ти показ-ля преломлен среды n от длины волны света l(от скорости распространения света).Отражение и преломлен света.При падении свет волны на плоскую границу раздела 2х диэлектриков с разными значениями относит-но диэл

ектрической проницаемости,свет волна частично отраж-ся и час

тично преломл-ся.Закон отражения:Угол падения равен углу отражения.Закон преломления:Луч падающ,преломлен и перпендикул к поверх-ти раздела 2х сред, восстановлен из точки падения луча лежат в одной плоскости и вып-ся соотношение: n -абс. пок-ль преломлен

n₂₁- относител показатель преломления. При определенном угле луч будет полностью отражаться обратно в стекло.Угол полного внутреннего отражения:

Поглощение света.Из-за рассеяния эн-гии в-во поглощает свет. В рез-те светов поток по мере распростран-я света в в-ве умень

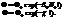ш-ся.Обычно суммарное эффективное сечение атомов в единице объема S₀N₀ наз коэффициентом поглощения среды, S₀N₀ = c.Это Закон Бугера:световой поток в поглощающей среде убывает по экспоненциальному закону.Фазовая и групповая скорость света.Встал вопрос об уточнении понятия ск-ти свет волны.

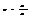
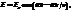Рэлей показал,что ур-ние плоской монохроматич волны: Фазовая ск-ть- ск-ть распространения фазы волны:

 

Групповая ск-ть– ск-ть переноса энергии световым сигналом. Пусть имеем две волны: колебания(волны) с близкими частотами:

 

 

фазовая скорость

групповая ск-ть(движ-я макс. амплитуды)

В отсутствии дисперсии U=u_Ф

U<u_Ф Нормальная дисперсия

U<u_Ф Аномальная дисперсия.

всегда U<C.

Рассеяние света.Среда явл-ся оптически однородной,если люб

ой элемент её объёма имеет постоянное для данной среды значе

ние показателя преломлен n. В идеальн оптически однородной среде не д.б. рассеяния света.Мутные среды–это среды, оптичес

ки неоднородные и интенсивно рассеивающие свет.Это туманы,

взвеси,эмульсии,перламутры.Опытные законы:**Чем короче длина волны λ,тем интенсивнее рассеив-ся свет. Если рассеяние наблюд-ся в белом свете,то рассеянный свет имеет сине-голубой оттенок.**Свет,рассеянный под прямым углом к первичному пу

чку естественного света,полностью или почти полностью линей

но поляризован.**Кривая интенсив-ти рассеянного света симме

трична относит-но направлений первичного пучка и перпендику

лярному ему.Рэлей:**Интенсивность рассеянного света пропорц

иональна шестой степени радиуса рассеивающих частиц. С увел

ичением размера частиц рассеяние быстро увеличивается.**Чем короче световые волны, тем сильнее они рассеиваются. Зависимость I_расс~1/λ⁴ наз законом Рэлея.       

 

 

---

Дата добавления: 2018-02-18; просмотров: 1028; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!