Элементы зонной теории твердого тела.
Современная теория твердого тела (ТТ) построена на ур-и Шредингера. Она рассматривает ТТ как многоядерную и многоэлектронную систему, в которой действуют кулоновские электрические силы. Магнитное взаимодействие между атомами в кристаллической решетке ТТ гораздо слабее, чем электрическое. Это позволяет часто им пренебрегать.
Точное решение у-я Ш для многоатомной и многоэлектронной сис-мы, каковой явл кристалл, упирается в непреодолимые математ. трудности. В физике ТТ задача решается с помощью прибл-ых методов. Их суть в том, что задача многих частиц сводится к одноэлектронной задаче.Вместо многих Эл-ов рассматр один электрон, движущийся в постоянном периодическом поле многих ядер (крист. решетки).
Энергетические зоны. Два одинаковых атома, бесконечно удаленные друг от друга, имеют тождественные энерг-ие уровни. Если эти атомы постепенно сближать, то из-за взаимного влияния их эл-их полей энергетические уровни атомов будут расщепляться. При образовании двухатомной молекулы группы таких расщепленных уровней образуют энергетические полосы.Max ширина полос опред min расст м/у двумя ближайшими атомами. Поэтому каждый последующий атом не делает полосы шире. Он лишь увеличивает число энергетических уровнейв постоянной по ширине полосе. Сильнее всего расщеп-я внешние уровни. Чем ниже уровень, тем слабее он расщепляется.
Энергия теплового движения примерно на 20 порядков превосходит ширину энергетических ступеней в полосе. Поэтому в нагретых кристаллах, то есть при Т>0К, Эл-ны в энерг полосах при наличии вакансий могут дрейфовать в пределах полос за счет энергии теплового движения. Поэтому такие полосы в кристаллах назыв энергетическими зонами. Различают разрешенные зоны, то есть зоны – полосы, состоящие из разрешенных уровней, на каждом из которых могут находиться Эл-ны, и запрещенные энерг-кие зоны, то есть области, где Эл-ны находиться не могут.
|
|
|
Энергетическую зону, возникшую из того уровня, на кот нах-ся валентные Эл-ны в основном (не возбужденном) состоянии атома, называют валентной зоной. В зав-ти от степени заполнения валентной зоны эл-ми и ширины выше расположенной запрещенной зоны возможны три случая:
1.Проводники(пример натрий). В изолированном и невозбужденном атоме натрия в 3s-состоянии находится один валентный Эл-н. Max возможное число Эл-в в 3s-состоянии =2. При объединении атомов натрия в кристалл уровни расщепляются, но соотношение м/д заполненными и свободными вакансиями сохраняется. В результате в кристалле натрия образ валентная зона, заполненная Эл-ми при температуре абсолютного 0 наполовину. Валентную зону в металлах называют зоной проводимости. Металлы (Au, Cu, Ag, Na, K, Li...).
|
|
|
Электр-я проводимость в кристаллах оказывается возможной потому, что валентные и более высокие разрешенные зоны соседних атомов в кристаллах перекрываются. Валентные электроны в кристаллической решетке металлов обобществляются между всеми атомами. В результате возникает зона проводимости, пронизывающая весь кристалл.
2.Диэлектрики(пример алмаз) В них при Т=0 эл-ны заполн валентную зону полностью. В кристалле сущ зоны двух типов: до конца заполн и совсем пустые. Такой кристалл при Т=0 не проводит эл-ий ток и является диэлектриком. При наложении на кристалл диэлектрика внешнего Эл поля (с напряженностью не большей напряженности пробоя кристалла), валентные Эл-ны в таких кристаллах остаются на своих местах, ибо нет близко распол своб уровней, на к-рые они могли бы перейти.
3.Полупроводники(пример кремний) Кристалл с заполненной при Т=0 валентной зоной при нагрев ведет себя по-разному в зависимости от ширины запр зоны Еg. Кристаллы с широкой запрещенной зоной являются диэлектриками вплоть до высоких температур. Твердых диэлектриков одноэлементного состава сравнительно мало. Это сера S, алмаз C, кристаллический азот N. Более распр высокотемпературными диэлектриками являются оксиды SiO2 (кварц), Al2O3 (глинозем) и др. Обычно к диэлектрикам относят кристаллы с шириной запрещенной зоны Еg>3эВ. Например, у алмаза Еg=5,2эВ, у глинозема Еg=7эВ.
|
|
|
Если ширина запр зоны невелика, так что при нагревании кристалла до нескольких сот кельвин тепловой энергии оказывается достаточно для перехода Эл-ов из валентной в свободную зону, то диэлектрик превращается в проводник. Свободная зона при переходе в нее Эл-ов становится зоной проводимости. Такие кристаллы с малой шириной запрещенной зоны называются полупроводниками (Еg~1эВ). При низких температурах они прибл к диэлектрикам, при высоких – к проводникам. Резкой границы м/у диэлектриками и полупроводн нет, и в реальных диэлектриках при Т>0 в зоне проводимости всегда есть некот кол-во эл-ов. Оно тем больше, чем меньше ширина запрещенной зоны и чем выше температура.
Поверхность Ферми. Сравним распределение Эл-нов проводимости в металлах с распределением Максвелла-Больцмана молекул идеального газа при Т=0.
Классический газ при Т=0 должен прекратить свое существование, поскольку энергия его частиц обращается в нуль, 
=3кТ/2=0.отсюда, обращается в 0 и скорость движения частиц. С Эл-ми проводимости при Т®0 энергия Эл-нов проводимости в кристалле не может стремиться к 0, т.к. все Эл-ны перейдут в одинаковое состояние с 0 энергией. Но это запрещено принципом Паули. При Т=0 эл-ны проводимости располагаются на энергетической лесенке, начиная с самой нижней ступеньки и плотно заполняя все разрешенные энергетические уровни так, что на каждом из них находится не более 2 эл-в.
|
|
|
Ф-я плотности вероятности q(Е) распред-ния Эл-ов проводимости в Ме по энергиям Е имеет вид:
Здесь V – объем кристалла, me – масса электронов, h – постоянная Планка.
График функции q(Е) показан на рис. Верхний из заполненных при Т=0К уровней зоны проводимости металла называют уровнем Ферми, а его энергию – энергией Ферми Еф. Величина Еф при Т=0 определяется выражением:
, n – концентрация свободных Эл-ов в Ме.
Распределение Максвелла-Больцмана для идеального газа при Т>0К выглядит как центрально – симметричная туманность в пространстве импульсов с увелич-ся к центру концентрацией частиц чем больше энергия частиц, тем дальше они от центра. При Т®0К туманность стягивается в центральную точку. С ростом температуры туманность увелич в размерах.
В отл от классич газа эл-ны в зоне проводимости Ме образуют в импульсном пространстве тело с гладкой при Т=0 поверх-ю. Ее называют поверхностью Ферми. Вид этой пов-ти существенно сказывается на многих электрич, магнитных и других св-вах Ме. Это позвол строить поверхность Ферми по эксперим-ым данным.
У одновалентных (щелочных) металлов поверхность Ферми имеет форму сферы. У двух валентных, имеет более сложн форму.
С ростом температуры распределение электронов по энергиям приближается к классическому. Критерием поведения электронного газа является температура вырождения
, n-концентрация, m- масса частиц, k-постоянная Больцмана,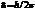 
- постоянная Планка.
При Т<Т0 газ называется вырожденным, его поведение описывается законами квантовой механики. След-но, при всех температурах сущ кристаллических проводников Эл-ны проводимости в Ме представляют собой вырожденный газ (Ферми-газ), подчиняющийся квантовым законам.
Если Т>Т0, то газ невырожден, по своим св-вам он приближается к классическому.
Парадокс теплоемкости металлов. Для твердых диэлектриков справедлив з-н Дюлонга- Пти: молярная теплоемкость всех твердых кристаллических веществ есть величина одинаковая для всех веществ, не зависящая от температуры и равная 3R.
Кл теория: каждый атом – узел крист-ой решетки можно уподобить упругому осциллятору, способному колебаться в 3-х взаимно перпендикулярных направлениях. Полагая осцилляторы гармоническими с непрерывно измен энергией, можно постулировать, что на каждое направление приходиться в среднем kT/2 кинет и kT/2 потен энергии осциллятора. Средняя энергия осциллятора:
.
В 1 моль кристалла входит число Авогадро NA атомов. Внутренняя энергия одного моля U= NA=3kNA·T=3RT, где R - универсальная газовая постоянная. Изохорная молярная теплоемкость
, что соответствует закону Дюлонга и Пти.
Теория Друде – Лоренца оказалась не в состоянии объяснить закон Дюлонга и Пти у Ме. Действительно, если в объеме кристалла наряду с атомами – узлами есть эл-ый газ, то теплоемкость кристалла должна складываться из теплоемкости этих двух систем частиц, находящихся в тепловом равновесии. Пусть на каждый атом приходиться z валентных Эл-ов. Тогда на 1 моль узлов приходится z молей эл газа. Молярная теплоемкость узлов – осцилляторов равна 3R, теплоемкость z молей идеального газа равна (3R/2)· z. Суммарная теплоемкость
CV=3R+3 z R/2. При z=1 CV=4,5R. Опыт показывает, что CV металлов, как и диэлектриков, ближе к 3R. В этом суть парадокса теплоемкости.
Кв теория объясняет этот парадокс. Средняя энергия Эл-ов проводимости на нижних заполненных уровнях составляет при Т=0К около 3 эВ. Средняя тепл энергия при нагревании на 1К примерно в 10000 раз меньше. Поэтому тепловой энергии, получаемой Эл-ми проводимости от узлов крист-ой решетки при нагревании кристалла, недостаточно для перевода эл-ов на верхние свободные уровни.Вклад в теплоемкость вносят лишь самые верхние Эл-ны проводимости, к-ые имеют сверху свободные энерг уровни с относительно малой шириной энергетического перехода.
Сверхпроводимость. В 1911г Оннес, измеряя сопротивление ртути в области низких температур, обнаружил, что при Т =4,2К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью.
Это явление не сводится к нормальному падению уд сопротивления бездефектного кристалла, когда rn=0, и rТ 
. Переход в сверхпроводящее состояние скачкообразно при некоторой температуре Ткр, которую называют критической температурой перехода.
Эффекты сверхпроводимости.
а. Электрический ток, возбужденный в сверхпроводящем кольце, может циркулировать в нем годами.
б. Эффект Мейснера. Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле, при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема. Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m=0.
Вещ-во в сверхпроводящем сост приобр два не связанные друг с др-м фунд-ые св-ва: идеальную проводи-ть и ид-ый диамагнетизм.
Если усиливать ток, идущий по сверхпроводнику, то при некотором его критическом значении Iкр сверхпроводящее состояние разрушается. Поскольку магнитное поле В пропорционально току I, то зависимость Iкр от температуры аналогична зависимости Вкр(Т).
г. Эффект Джозефсона. Джозефсон теоретически предсказал два эффекта
Подсоединим к сверхпроводнику (он изображается в виде бруска) амперметр А с источником постоянного тока e и вольтметр V. При замыкании ключа Кл в цепи возникает постоянный ток, регистрируемый амперметром. Т.к. сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль.Разрежем сверхпроводник на две части и раздвинем их так, чтобы между ними возник диэлектрический зазор толщиной d»1нм. Как предсказал Джозефсон, при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов.Стационарный эффект Джозефсона. Ч/з сверхпроводник по-прежнему протекает постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка.Нестационарный эффект Джозефсона. На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов. В этом случае из щели излучается высокочастотная электромагнитная волна.Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток.
Теория сверхпроводимости. Ее построили Бардин, Кулер и Шриффер. По первым буквам их фамилий ее назвали БКШ – теорией. В основе БКШ - теории лежит представл, что м/у Эл-ми проводимости Ме могут действ силы притяжения, возник вследствие поляризации ими кристаллической решетки.
Можно предположить, что сверхпр-ть следует ожидать прежде всего у тех Ме, у которых имеет место сильное взаимод эл. газа с решеткой, привод в обычных условиях к высокому удельн сопрот.
Как показал Купер, при Т<Ткр, самые верхние Эл-ны, распол на уровне Ферми, могут спариваться. При этом их суммарная энергия оказ меньше суммы энергий отдельных электронов. Выдел-ся энергия дол отводиться от кристалла охл-ем. Понижение энергии куперовских пар приводит к понижению верхнего занятого эл-ми уровня. В рез-те м/д уровнями куперовских пар и ближайшими свобод уровнями возникает запрещ зона шириной 2D. Эта возникшая энерг-ая щель не позвол куперовским парам эл-ов принимать малую энергию. Они могут принять лишь энергию не менее 2D, кот-я позволит эл-ам перепрыгнуть через эту щель. Поэт при Т<Ткр купер-ие пары оказываются весьма устойчивыми.
При Т<Ткр спариваются не все эле-ны. При каждой темп-ре устанав некот равновесное соотн м/д концентрациями норм и спаренных эл-ов. Оказ-ся, что ширина 2D энерг-ой щели в сверхпроводнике зависит от кол-ва неспаренных эл-ов. Их концентрация понижается с уменьшением температуры и соответственно растет ширина щели.
Эл-ны, образующие куперовские пары, имеют противопол спины. Поэтому спин пары равен нулю, и она представл собой бозон. Бозоны могут накапливаться в основном энерг-ком состоянии, из кот-го их трудно перевести в возбужд сост. Поэтому куперовские пары в сост согласованного движен м. оставаться неопределенно долго. Такое согласованное движение пар и есть ток сверхпр-ти.
Дата добавления: 2018-02-18; просмотров: 1044; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!