Теорема о равномерном распределении энергии по степеням свободы.

⇐ ПредыдущаяСтр 8 из 17Следующая ⇒

Теплоемкостью тела называют величину C, численно равную количеству тепла, которое нужно подвести к телу или отнять от него для изменения его температуры на 1К. . Различают ещё молярную теплоемкость C = С|n и удельную теплоемкость с = С| m, где n и m – количество вещества в теле и его масса. Еденица измерения молярной теплоемкости – Дж| (моль×К), единица измерения удельной теплоемкости – Дж| (кг×К).

Если M – молярная масса вещества, между ними такая связь: C = c×M, Поскольку нагревание тел и особенно газов можно проводить как при постоянном объеме, так и при постоянном давлении, то различают изохорную и изобарную теплоемкости. Изохорная теплоемкость газа

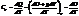Изохорная теплоемкость тела (системы) определяется лишь изменением его внутренней энергии, C_v = dU| dT. Изобарная больше на величину работы расширения тела. Для вычисления этой работы в случае ИД выразим объем газа V из уравнения Клапейрона-Менделеева, V = nRT| p. Продифференцируем по температуре.

Подставив получаем C_p = C_v+R –уравнение Майера.

Универсальная газовая постоянная R численно равна работе изобарного расширения одного моля идеального газа при нагревании на 1 К. В термодинамике широко применяется величина, равная отношению теплоемкостей, показатель адиабаты

Теорема о равномерном распределении энергии по степеням свободы. Классическая теория теплоемкости основана на предположении, что к атомно-молекулярным сист применимы законы класс Ньютоновой механики. Постулат Больцмана:Если система молекул находится в тепловом равновесии при температуре T, то средняя механическая энергия равномерно распред по всем степеням свободы и для каждой степени свободы каждой молекулы она равна ¹/₂kT. Если всего степеней свободы i, то средняя кинет энергия каждой молекулы составляет ⁱ/₂kT.

Теплоемкость одноатомных газов средняя кинетическая энергия молекул идеального газа составляет .Полагаем их материальными точками, у них по 3 степени свободы. Тогда на каждую степень свободы приходится в среднем энергия . Внутренняя энергия одноатомного идеального газа

Изохорная молярная теплоемкость

Изобарная молярная теплоемкость .

Ппоказатель адиабаты

Теплоемкость двухатомных газовАтомы скреплены между собой упругим стержнем. К трём степеням свободы поступательного движения таких молекул добавляются две степени вращательного Всего степеней свободы . Тогда

Теплоемкость многоатомных газов Многоатомными считаются молекулы с числом атомов 3 и более. Благодаря тому, что валентные связи атомов образуют углы, отличные от 180˚, атомы в молекулах газов не располагаются вдоль одной прямой. Поэтому такие молекулы можно рассматривать как систему материальных точек, жестко связанных между собой и образующих пространственную фигуру. При не очень больших скоростях движения эти фигуры можно моделировать абсолютно твердыми телами с 6 степенями свободы. Кроме 3 степеней свободы поступательного движения молекула имеет три степени вращательного движения. Тогда

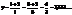
твердое тело - кристалл. В твердом теле атомы совершают колебания около положения равновесия. Каждый м колебаться в 3х взаимно перпендикулярных направлениях=>полагаем кристалл системой из 3N независимых гармонических осцилляторов с непрерывно изменяющейся энергией. По теореме о равномерном распределении энергии по степеням свободы ср тепловая энергия одного узла . Внутренняя энергия одного моля кристалла =3RT. Изохорная молярная теплоемкость (з-н Дюлонга и Пти).Молярная теплоемкость всех ТВ тел есть величина одинаковая для всех веществ, не зависящая от тем-ры и равная 3R.

Однако в классической теории существует ряд затруднений: При описании газов: 1). Согласно III началу термодинамики все теплоемкости должны приближаться к 0, если Т®0, а вточке, где Т=0, должны =0. В ходе эксперим. для двухатомных газов теор.= 7/2R.практика=5/2R.При дальнейшем уменьшении Т теп-сть падала до 3\2R. Теор анализ экспер показыв: при высокихТ кол-я не возб-ся =5/2R при низких Т вымерзают и вращ-е степ свободы остается только поступательная.

2). При описании тв тел по теории: с_v=c_v(решетки.)+c_v(электр.газ) . Эксперимент дает c_v=3R(закон Дюлонга и Пти.), кроме того, вблизи абсолютного 0 c_v~T³. Для диэлектрика мы имеем 7/2R по теории а на практике получаем график. При понижении темп-ры теплоемкость падает, пока не достигнет 3/2R , здесь она задерживается, но потом снова падает. Это можно объяснить так: в двухатомных молекулах выключена колебательная степень своб. Классич теория не может объяснить отступления от з-на Дюлонга и Пти. Это удается сделать лишь в рамках квантовых представлений.

Проблема расхождения теории и эксперимента была снята работой Энштейна в 1905 г. Используя гипотезу квантов Планка он показал, что ход теплоемкости можно объяснить, если предположить дискретность уровней энергии для колеблющихся частиц. Было выяснено поведение теплоемкости ид. Газов

Было выяснено, что при высоких температурах для теплоемкостей получаем классический результат, при низких температурах другой. Кроме того, открытие Ферми-газа и Бозе-газа объяснило аномальный ход теплоемкости. Проблема теп-ти эл-го газа снята – он вырожден и его теп-ть мала, т.к. ничтожное число е-ов – активны.

Квант теория колебаний крист решетки.Модель решетки: 1. Реш-ка сос-т из N атомов, кажд атом совершает 3 независимых кол-я, т.о. вместо решетки рассматриваем совок-ть 3N гармонич осцилляторов. 2. В квант-м случае дополнение: все осцилляторы кол-ся с одной и той же частотой Согласно кв мех-ке эн-ия осциллятора квантуется по з-ну , где n=0,1,2... Видно, что мы получили рез-т, в корне отличающийся от классического, т.к. по классич теории Е одной колебат степени свободы =кТ и не зависит от частоты. Но нас интерес-т тепл-ть. 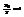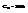Рассмотрим комбинацию: => или В этой области: => При больших темпер-х рез-ты квантов теории не расходятся с классич теорией и эксперим-м. Расс-м случай: -низкие темпер-ры. В знаменателе выражения единицей можно пренебречь. Экспонента убывает быстрее, чем График: С_V от Т, прямая линия С_V=3Nk –классика. Меньше T₀ – убыв. до 0.

Квантовые осцилляторы. Формула Планка. Планк предположил, что энергия узлов в кристалле изменяется не непрерывно, как у макротел, а порциями величиной hv, где v – частота колебаний осциллятора, h – постоянная Планка, называемая квантом действия, h = 6,6×10^-³⁴ Дж×с. Планк предположил, что осцилляторы, колеблющиеся в данном направлении, распределены по энергиям ε в соответствии с законом Больцмана. 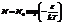,где N₀ – число осцилляторов с нулевой энергией. средняя энергия квантовых осцилляторов, колеблющихся вдоль одного направления, равна

.Макс Планк.

многократно вырождены. Кроме того н. учитывать и внутр-ие степени свободы, мы возьмем только спин. Спектр квант состоя-ний и уровней эн-ии у всех час-ц одинаков.

Дата добавления: 2018-02-18; просмотров: 2311; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!