Построение  оптимального  портфеля ценных  бумаг  при рискованных и  безрисковых вложениях. Задача Д.Тобина (J.Tobin).

Постановка задачи.

 

Ценные бумаги, входящие в портфель инвестора, можно разделить условно на две группы. В первую группу войдут ценные бумаги, имеющие малый риск и умеренную доходность. Во вторую группу войдут ценные бумаги, имеющие большую доходность и соответственно больший риск. Бумаги, имеющие малую доходность и больший риск, очевидно, не следует включать в портфель.

К безрисковым ценным бумагам можно отнести государственные ценные бумаги. В частности, на рынке США это вексель казначейства (US Treasury Bill), расписки казначейства (US Treasury Notes), бона казначейства (US Treasury bonds).

Тобин Д. рассмотрел следующую предельную ситуацию, когда инвестор выделяет х₀ денег на приобретение государственных ценных бумаг с ожидаемой доходностью г₀ и нулевым риском. Остальные 1-х₀ денег инвестор тратит на рискованные ценные бумаги, например акции, с ожидаемой доходностью m_i большей, чем эффективность безрисковых бумаг г₀, т. е. m_i>r₀ (i=1,2,...,n).

Математическая постановка задачи следующая.

Требуется найти распределение средств инвестора х₀, x₁, х₂..., х_пмежду безрисковыми и рискованными бумагами 1, 2,..., птакое, что выполняются линейные ограничения:

х₀ + х_] + х₂ +... + х_п = 1 (уравнение баланса)                               (3.1)

m_ох_о + m₁х₁ + m₂х₂ +... + m_пх_п = m_s                                                                   (3.2)

(фиксация ожидаемой суммарной доходности портфеля акций на уровне т_s)

и минимизируется риск, равный

V=v₁₁x₁²+v₂₂x₂²+...+v_nnx_n²+2(v₁₂x₁x₂+v₁₃x₁x₃+…+v_n-1,n x _n-1x_n),        (3.3)

где  - риск i-ой ценной бумаги (дисперсия эффективности i-ой ценной бумаги) i=1,2,…n.,

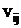- ковариация i-ой и j–ой ценной бумаги, определяющая связь между эффективностями i-ой и j–ой ценной бумагой i=1,2,…n, j =1,2,…n.

Аналитическое решение задачи построения оптимального портфеля (задача Д.Тобина).

 

Рассмотрим упрощенную постановку задачи Д.Тобина (J.Tobin). Инвестор формирует портфель из четырех ценных бумаг, одна из которых является государственной безрисковой ценной бумагой. Средняя доходность портфеля m выражается формулой:

m = x₀+5x₁+11x₂+21x₃,                                                 (3.4)

где: х₀ – доля государственных безрисковых ценных бумаг,

х₁, х₂, х₃ – доля ценных бумаг 1, 2, 3 с ненулевым риском (например акций).

При этом выполняется уравнение баланса:

х₀+х₁+х₂+х₃ = 1                                             (3.5)

Риск портфеля зависит только от количества рискованных ценных бумаг (акций) и их рисков:

σ²= х₁²+2х₂²+5х₃²                                                                                (3.6)

 

Задача Д.Тобина в этом случае имеет вид. Найти структуру x₀  x_1, x₂, x₃ портфеля ценных бумаг, обеспечивающую минимальный риск (3.6), при выполнении линейных ограничений: уравнения баланса (3.5) и фиксации доходности m = const (3.4). Определить риск оптимального портфеля инвестора.

Решение:

Вычитая из уравнения доходности (3.4) уравнение баланса (3.5), получим уравнение не содержащее переменной х₀.

(x₀+5x₁+11x₂+21x₃)-( х₀+х₁+х₂+х₃)=m-1

                   4 x₁ + 10 x₂ + 20 x₃ = m-1                          (3.7)

Таким образом, задача упрощается. Нужно найти минимум функции риска (3.6) при одном ограничении (3.7).

Воспользовавшись функцией Лагранжа, получим:

L = х₁²+2 х₂²+5 х₃²  - λ (4 x₁ + 10 x₂ + 20 x₃ - (m-1))

где λ – множитель Лагранжа.

Для достижения минимального значения вычислим и приравняем к нулю частные производные от функции Лагранжа:

и в результате для х имеем:

x₁ = 2λ, x₂ = 2,5 λ,          x₃ = 2 λ                   (3.8)

Для вычисления множителя Лагранжа λ, подставим значения (3.8) в ограничения (3.7) и вычисляем значение множителя Лагранжа λ:

Подставляя значение λ в (3.8), вычисляем относительное количество средств потраченных на рискованные и государственные безрисковые ценные бумаги (значения х₁,х₂,х₃,х₀ ):

x₁ = (m-1) = 0,02739(m-1)

x₂ = (m-1) = 0,03424(m-1)                (3.9)

x₃ = (m-1) = 0,02739(m-1)

x₀ =1 - 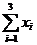(m-1) =1- 0,08902(m-1)

       Для риска σ² из (3.6) и (3.9) получим:

σ² = х₁²+2х₂²+5х₃²= (m-1)²,

Следовательно, среднеквадратическое отклонение σ равно:

σ = =  = 0,08276 (m-1)

В качестве численного примера рассмотрим случай, когда желаемая доходность портфеля равна m=1, 2, 3, 11

 

m	1	2	3	11
x1	0	0,02739	0,05478	0,2739
x2	0	0,03424	0,06848	0,3424
x3	0	0,02739	0,05478	0,2739
x0	1	0,91098	0,82196	0,1098
σ	0	0,08276	0,16552	0,8276

    Таблица 3.1

Зависимость структуры портфеля и риска от доходности портфеля.

 

На рис.3.1. представлена зависимость структуры портфеля х₀, х₁, х₂, х₃ от доходности портфеля m. Прямые для х₁ и х₃ совпадают.

 

На рис.3.2. представлена зависимость риска портфеля σ от доходности портфеля m.

 

 

При доходности портфеля m = 1, равной доходности государственной ценной бумаги, получается очевидный результат х₀=1, х₁=0, х₂=0, х₃ =0,

 т. е. все средства следует вложить в государственную ценную бумагу. При увеличении желаемой доходности портфеля средства начинают понемногу перетекать из государственной ценной бумаги в акции, причем пропорция между средствами на акции будет постоянной на первую и третью акцию одна и та же сумма на вторую акцию в 1,25 раз больше.

Таким образом, структура портфеля ценных бумаг не меняется в зависимости от желаемой доходности портфеля ценных бумаг. Пропорция: х₁:х₂:х₃ не зависит от желаемой доходности портфеля ценных бумаг. Это свойство портфеля остается справедливым и в общем случае.

В общем случае задача оптимизации портфеля ценных бумаг решается численными методами, например, с помощью программы поиск решения из Excel. Для её подключения необходимо произвести следующие операции: войти в Excel, далее Сервис / Надстройки /Поиск решения.

---

Дата добавления: 2018-02-15; просмотров: 1070; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!