Аналитическое решение упрощенной задачи построения оптимального портфеля с минимальным риском (задача об осторожном инвесторе)
В качестве численного примера рассмотрим решение задачи для случая трех ценных бумаг:
Портфель состоит из 3х независимых ценных бумаг, и описываться следующими уравнениями:
x1+x2+x3=1 (уравнение баланса); (2.5)
m=10 x1+20 x2+40 x3 (уравнение дохода) (2.6)
При этом риск портфеля будет равен:
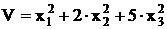(уравнение риска) (2.7)
Найдем структуру портфеля ценных бумаг обеспечивающую минимальный риск (2.7) при выполнении линейного ограничения уравнения баланса (2.5). Определить доходность оптимального портфеля осторожного инвестора.
Поиск оптимального портфеля ценных бумаг производиться методом Лагранжа. Функция Лагранжа будет равна:
,
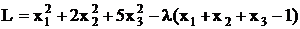где λ - множитель Лагранжа. Вычислим частные производные:
, 
, 
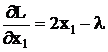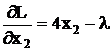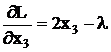
Отсюда, приравнивая к нулю производные, получим структуру портфеля ценных бумаг:
, 
, 
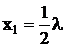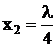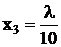
Для определения множителя Лагранжа λ воспользуемся уравнением баланса (2.5):
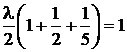
Окончательно имеем:
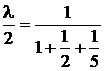
Тогда структура портфеля приобретет вид:
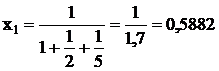
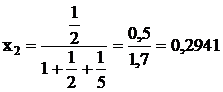(2.8)
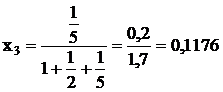
Подставим значения x в уравнения (2.6) и (2.7), и найдем значения дохода и риска оптимального портфеля:
m=10∙0,5882+20∙0,2941+40∙0,1176=5,882+5,882+4,70588=16,4706
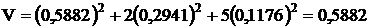
Представим полученные результаты в виде таблицы. Первая строка соответствует оптимальному портфелю осторожного инвестора. Вторая, третья и четвертая строки предполагает вложение всех средств в первую, вторую и третью ценную бумагу соответственно
|
|
|
| x1 | x2 | x3 | m | V |
| 0,5882 | 0,9241 | 0,1176 | 16,4706 | 0,5882 |
| 1 | 0 | 0 | 10 | 1 |
| 0 | 1 | 0 | 20 | 2 |
| 0 | 0 | 1 | 40 | 5 |
Если поверхностно подойти к задаче, то кажется, что минимальный риск достигается в случае, когда все средства вкладывать в наименее рискованную первую ценную бумагу. При этом доходность достигает 10, а риск достигает 1. Однако в случае оптимальной диверсификации следует вложить 58,8% в первую ценную бумагу, во вторую 29,4% и в третью 11,8%. При этом оказывается, что доход портфеля возрастет более чем в 1,5 раза и будет равен 16,46, а риск уменьшиться почти в два раза и будет равен 0,588.
Численное решение с помощью Excel задачи об осторожном инвесторе
Произвести расчет своего варианта финансового инвестиционного проекта:
См. варианты_инв_курс_пр.xls, лист2
· Получить аналитическое решение своего варианта задачи об осторожном инвесторе
· Произвести численный расчет оптимального портфеля острожного инвестора с помощью программы оптимизации Excel «Поиск решения ». Для её подключения необходимо произвести следующие операции: войти в Excel, далее Сервис / Надстройки /Поиск решения.
|
|
|
· Сравнить аналитическое и численное решение задачи об осторожном инвесторе
См. инвестиции_курс_пр.xls, лист3
Численное решение с помощью Excel задачи построения оптимального портфеля (задача Г.Марковица - общий случай)
В качестве численного примера рассмотрим решение задачи для случая трех ценных бумаг с параметрами своего варианта.
См. варианты_инв_курс_пр.xls, лист2
Портфель состоит из 3х независимых ценных бумаг, и описываться следующими уравнениями:
x1+x2+x3=1 (уравнение баланса); (2.9)
m=m1 x1+ m2 x2+ m3 x3 (уравнение дохода) (2.10)
При этом риск портфеля будет равен:
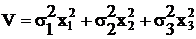(уравнение риска) (2.11),
где x1, x2, x3 - доля средств, потраченных на приобретение 1, 2 и 3-ей ценной бумаги,
mi - средняя доходность i-ой ценной бумаги (математическое ожидание эффективности i-ой ценной бумаги) i=1,2,3,
- риск i-ой ценной бумаги (дисперсия эффективности i-ой ценной бумаги) i=1,2,3,
Задача Г.Марковица в этом случае имеет вид. Найти структуру x1, x2, x3 портфеля ценных бумаг, обеспечивающую минимальный риск (2.7), при выполнении линейных ограничений: уравнения баланса (2.9) и фиксации доходности (2.10). Определить риск оптимального портфеля инвестора.
|
|
|
Для своего варианта
· Численными методами произвести расчет оптимального портфеля инвестора с помощью программы оптимизации Excel «Поиск решения ». Рассмотреть несколько вариантов доходности портфеля. Определить риск оптимального портфеля инвестора
· Определить структуру x1, x2, x3 и риск 
оптимального портфеля инвестора для четырех - восьми значений доходности m портфеля из вашего варианта
· Построить графики зависимости структуры x1, x2, x3 и риска портфеля от доходности m оптимального портфеля.
· Рассмотреть случай, когда дополнительно используются ограничения (2.4) в виде неравенств 
. Определить риск и структуру оптимального портфеля.
· Построить графики зависимости структуры x1, x2, x3 и риска портфеля от доходности m оптимального портфеля для случая когда .
- На основании полученных результатов сделать выводы о свойствах оптимального портфеля в задаче Г.Марковица.
См. инвестиции_курс_пр.xls, лист4
См. Optimal.exe
Дата добавления: 2018-02-15; просмотров: 1184; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!