Построение оптимального портфеля ценных бумаг при рискованных вложениях. Задача Г.Марковица (H.Markowitz).

 

Портфелем ценных бумаг инвестора называется совокупность некоторого количества ценных бумаг различного типа – акций нескольких корпораций, векселей, контрактов, опционов и т.д.

Финансовая операция (сделка) называется рискованной, если ее эффективность недетерминирована, т.е. не известна в момент заключения сделки. В этом случае эффективность финансовой сделки является случайной величиной и зависит от случайных обстоятельств.

Другими словами рискованную финансовую сделку нельзя характеризовать каким-либо одним значением эффективности. Рискованной сделке соответствует целый ансамбль возможных значений эффективности, реализующихся с той или иной степенью вероятности.

Если удается получить некоторые вероятностные характеристики эффективности сделки, то может быть поставлена задача ограничения или минимизации риска при заданном уровне доходности сделки.

Одна из целей курсового проекта является построение оптимального портфеля ценных бумаг при рискованных инвестициях, и таким образом, в частном случае, получить решение задачи Г. Марковица (H.Markowitz).

 

Постановка задачи оптимизации портфеля ценных бумаг.

 

Распределить средства, выделяемые на покупку ценных бумаг так, чтобы при фиксированной эффективности портфеля обеспечить минимальный риск;

Математическая постановка задачи следующая.

Найти структуру портфеля ценных бумаг x₁, x₂, ¼, x_n,, удовлетворяющую линейным ограничениям:

x₁+x₂+¼+x_n=1                        (уравнение баланса);                  (2.1)

x₁m₁+x₂m₂+¼+x_nm_n=m_s     (фиксация эффективности)       (2.2)

и минимизирующие квадратичную функцию риска

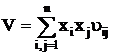.                                                                                   (2.3)

где x_1, x₂,¼x_n   - доля средств, потраченных на приобретение 1, 2, ¼, n-ой бумаги,

m_i - средняя доходность i-ой ценной бумаги (математическое ожидание эффективности i-ой ценной бумаги) i=1,2,…n,,

 - риск i-ой ценной бумаги (дисперсия эффективности i-ой ценной бумаги) i=1,2,…n,

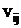- ковариация i-ой и j–ой ценной бумаги, определяющая связь между эффективностями i-ой и j–ой ценной бумагой i=1,2,…n, j =1,2,…n,.

Решение этой задачи может содержать некоторые значения x_n<0. Это означает, что при формировании оптимального портфеля для покупки k-ой ценной бумаги следует взять в долг сумму – x_n. Если портфель ценных бумаг уже существует, то следует продать пакет из n-ых ценных на сумму – x_n.

Если в долг брать нельзя, то дополнительно к ограничениям равенствам в задаче оптимизации добавляются ограничения неравенства:

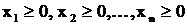.                                                    (2.4)

Рассмотрим сначала задачу построения оптимального портфеля инвестора без ограничения (2.4). Если в задаче оптимизации портфеля на переменные не наложено условие неотрицательности, то задача имеет точное аналитическое решение.

 

---

Дата добавления: 2018-02-15; просмотров: 625; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!