Полиномиальные фильтры Чебышева
Если в качестве функции фильтрации в формулах (1) и (2) использовать полином Чебышева, обозначаемый 
, то формулы примут вид:
, (5) где 
- полином Чебышева степени (порядка) m;
ε – коэффициент неравномерности ослабления, определяемый по формулам (3) или (4).
Фильтры с данными частотными характеристиками называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов . Ниже приведены шесть первых полиномов Чебышева:
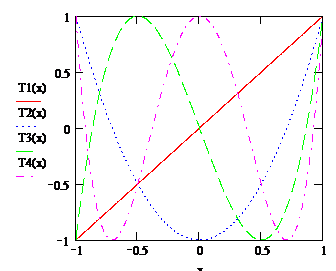
Любой полином Чебышева при 
может быть вычислен по рекуррентной формуле: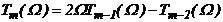 
. Таким образом, выражения (5) удовлетворяют общим выражениям характеристик полиномиальных фильтров и при Ω > 1 значения полиномов резко возрастают.
Существует единая тригонометрическая форма записи полиномов Чебышева в интервале 
:
(6)
Вне этого интервала полиномы также представляются в тригонометрической форме:
(7)
Анализ поведения полиномов Чебышева показывает, что в интервале угол 
изменяется от –π до π, поэтому полином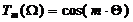 
ровно m раз принимает значения, равные нулю, и m+1 раз достигает значений, равных +1 или -1 и чередующихся друг с другом. Вне интервала полином монотонно возрастает быстрее всех других полиномов такого же порядка.
Рабочее ослабление фильтра Чебышева на тех частотах 
, где полином обращается в нуль, также обращается в нуль. На частотах, на которых равен 
, рабочее ослабление достигает величины:
|
|
|
.
С ростом значений полинома на частотах 
рабочее ослабление 
также монотонно растет. Приведем для примера график рабочего ослабления фильтра Чебышева четвертого порядка: При нечетном n график ослабления начинается с 0, при четном с
Армах=ΔА. Количество экстремумов в ПП с учетом граничной частоты равноn+1. .
Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.
Чтобы характеристики фильтра отвечали требованиям в полосе непропускания, необходимо выбрать порядок фильтра m из условия 
. Для полосы непропускания определяется формулой (7), следовательно, 
. Проведя ряд преобразований получим: 
. В этой формуле величина 
измеряется в неперах. При использовании единицы децибел порядок фильтра вычисляется из выражения:
Для формирования рабочей передаточной функции по Чебышеву поступаем аналогично выше изложенному :
определяется корнями уравнения 
, лежащими в левой полуплоскости:
,
где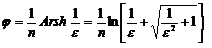 
.
Таким образом,
Сравнение фильтров Баттерворта и Чебышева
Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полиномами наилучшего приближения. Это означает, что при одинаковом значении m из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают 
, наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях m и 
.При заданных требованиях по ослаблению в ПН фильтр Чебышева может иметь меньший порядок чем у Баттерворта. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов. Фильтр Баттерворта из за этого более прост в настройке и изготовлении. Так же у него более линейна фазовая характеристика.
Дата добавления: 2018-02-15; просмотров: 736; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!