Случайная компонента (отклонение фактического значения уровней от их выровненных значений)
а) не подвержена автокорреляции;
б) подвержена автокорреляции;
в) зависит от метода выравнивания.
Г) а, в.
125. Формула для расчета коэффициента корреляции, исключающая влияние автокорреляции, имеет вид:
а)  ; б)
; б) 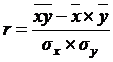 ; в)
; в)  ; г)
; г)  ; е) а, б; ж) в, г.
; е) а, б; ж) в, г.
126. Авторегрессия это:
а) зависимость величины уровня динамического ряда от предыдущих значений уровня в  моменты времени;
моменты времени;
б) взаимосвязь между уровнями двух взаимосвязанных рядов;
в) взаимосвязь между уровнями невзаимосвязанных рядов.
127. При наличии автокорреляции невозможно провести:
а) экстраполяцию будущих уровней нечетных лет;
б) экстраполяцию будущего уровня следующего периода;
в) экстраполяцию будущих уровней, минуя промежуточные уровни.
При линейной функции данная зависимость выражается как
а)  ;
;
б)  ;
;
в)  .
.
129. В статистике под индексом понимается:
а) абсолютный статистический показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве, в сравнении фактических величин с эталоном;
б) относительный статистический показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве, в сравнении фактических величин с эталоном;
в) а, б.
130. Индивидуальные индексы служат для характеристики:
а) изменения отдельных элементов сложного явления;
б) сложного явления, составные части которого непосредственно несоизмеримы;
|
|
|
в) а, б.
131. Сводные (общие) индексы служат для характеристики:
а) изменения отдельных элементов сложного явления;
б) сложного явления, составные части которого непосредственно несоизмеримы;
в) а, б.
132. В международной практике количество (объем) принято обозначать:
а) 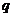 ; б)
; б) 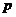 ; в)
; в)  ; г)
; г) 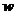 ; д)
; д) 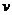 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
133. В международной практике себестоимость единицы продукции принято обозначать:
а) 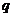 ; б)
; б) 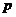 ; в)
; в)  ; г)
; г) 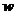 ; д)
; д) 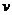 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
134. В международной практике цену единицы товара принято обозначать:
а) 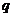 ; б)
; б) 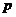 ; в)
; в)  ; г)
; г) 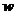 ; д)
; д) 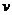 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
135. В международной практике выработку продукции в стоимостном выражении на одного рабочего или в единицу времени принято обозначать:
а) 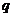 ; б)
; б) 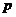 ; в)
; в)  ; г)
; г) 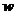 ; д)
; д) 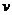 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
136. В международной практике выработку продукции в натуральном выражении на одного рабочего или в единицу времени принято обозначать:
а) 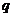 ; б)
; б) 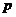 ; в)
; в)  ; г)
; г) 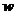 ; д)
; д) 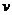 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
137. В международной практике общие затраты времени или численность рабочих принято обозначать:
а) 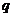 ; б)
; б) 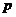 ; в)
; в)  ; г)
; г) 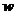 ; д)
; д) 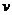 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
138. В международной практике стоимость продукции или товарооборот принято обозначать:
|
|
|
а) 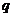 ; б)
; б) 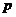 ; в)
; в)  ; г)
; г) 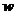 ; д)
; д) 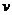 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
139. В международной практике издержки производства принято обозначать:
а) 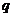 ; б)
; б) 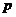 ; в)
; в)  ; г)
; г) 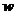 ; д)
; д) 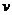 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
140. Используя международную практику обозначения индексируемых показателей, индекс физического объема продукции рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
141. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс цен продукции рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) 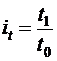 ; е)
; е)  .
.
142. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс себестоимости единицы продукции рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
143. Используя международную практику обозначения индексируемых показателей, индекс количества продукции, произведенной в единицу времени, рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
144. Используя международную практику обозначения индексируемых показателей, индекс производительности труда по трудовым затратам рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
145. Используя международную практику обозначения индексируемых показателей, индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего рассчитывается:
|
|
|
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  .
.
146. Числитель и знаменатель агрегатного индекса состоит из:
а) произведения двух индексируемых величин;
б) сумм двух индексируемых величин;
в) суммы индексируемой величины и веса индекса;
г) произведения индексируемой величины и веса индекса.
147. Индексируемая величина в числителе и знаменателе индекса:
а) остается неизменной;
б) изменяется;
в) не меняется в зависимости от величины индексируемой величины.
148. Вес индекса в числителе и знаменателе индекса постоянного состава:
а) остается неизменной;
б) изменяется;
в) меняется в зависимости от величины индексируемой величины.
149. Агрегатный индекс стоимости продукции (товарооборота)  рассчитывается:
рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 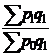 ;
;
д) а, б; е) б, г; ж) в, г.
150. Агрегатный индекс физического объема продукции 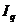 рассчитывается:
рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) а, б; е) б, г; ж) в, г.
151. Агрегатный индекс цен  рассчитывается:
рассчитывается:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) а, б; е) б, г; ж) в, г.
152. К индексам переменного состава относится:
а)  ; б)
; б)  ;
;
в) а, б.
153. К индексам постоянного состава относится:
|
|
|
а)  ; б)
; б)  ; в)
; в)  ;
;
г) а, б; д) а, в; е) в, б.
154. Средний индекс – это:
а) индекс, вычисленный как средняя величина из агрегатных индексов;
б) индекс, вычисленный как средняя величина из индивидуальных индексов;
в) зависит от величины индексируемой величины.
155. Средний индекс физического объема:а)  ; б)
; б)  ; в)
; в) 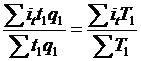 ; г)
; г)  ; д)
; д) 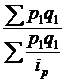 ; е) а, в.
; е) а, в.
156. Средний индекс производительности труда:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 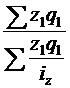 ; д)
; д)  ; е) а, в.
; е) а, в.
157. Средний индекс цен:
а) 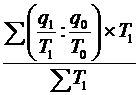 ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 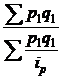 ; е) а, в.
; е) а, в.
158. Средний индекс себестоимости:
а)  ; б)
; б) 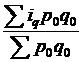 ; в)
; в)  ; г)
; г) 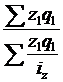 ; д)
; д) 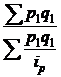 ; е) а, в.
; е) а, в.
159. Системой индексов называется:
а) любой ряд последовательно построенных индексов;
б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения;
в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения.
160. Системой цепных индексов называется:
а) любой ряд последовательно построенных индексов;
б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения;
в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения;
161. Системой базисных индексов называется:
а) любой ряд последовательно построенных индексов;
б) только ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения;
в) только ряд последовательно вычисленных индексов одного и того же явления с меняющейся от индекса к индексу базой сравнения.
162. Между индексом издержек производства  и индексами себестоимости
и индексами себестоимости 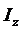 и физического объема
и физического объема  продукции существует следующая взаимосвязь:
продукции существует следующая взаимосвязь:
а)  ; б)
; б)  ; в)
; в)  .
.
163. Между индексом затрат времени на производство продукции  и индексами физического объема продукции
и индексами физического объема продукции 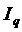 и индексом трудоемкости
и индексом трудоемкости  существует следующая взаимосвязь:
существует следующая взаимосвязь:
а)  ; б)
; б) 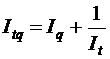 ; в)
; в)  .
.
164. Индекс физического объема продукции равен:
а) произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых);
б)  ;
;
в)  ;
;
г) 
д) а, б; е) а, г.
165. Дефлятор – это:
а) коэффициент, переводящий значения стоимостного показателя за отчетный период в стоимостные измерители базисного;
б) коэффициент, переводящий значения стоимостного показателя за отчетный период в стоимостные измерители отчетного;
в) а, б.
166. Индекс-дефлятор рассчитывается как отношение фактической стоимости продукции отчетного периода к стоимости объема продукции:
а) структура которого аналогична структуре отчетного года, но определенного в ценах базисного года;
б) структура которого аналогична структуре отчетного года, определенного в ценах отчетного года;
в) структура которого аналогична структуре базисного года, но определенного в ценах отчетного года.
167. В основе индекса-дефлятора лежит:
а) формула Пааше;
б) формула Ласпейреса;
в) формула Струмилина.
168. Выборочным наблюдением называется наблюдение, при котором:
а) обследованию подвергается вся исследуемая совокупность;
б) обследованию подвергается часть исследуемой совокупности;
в) обследованию подвергаются только качественные признаки совокупности;
г) а, б.
169. Выборочная совокупность – это:
а) часть единиц генеральной совокупности подлежащих наблюдению;
б) часть единиц генеральной совокупности не подлежащих наблюдению;
в) все единицы изучаемой совокупности;
г) а, б.
170. Генеральная совокупность – это:
а) часть единиц генеральной совокупности подлежащих наблюдению;
б) часть единиц генеральной совокупности не подлежащих наблюдению;
в) все единицы изучаемой совокупности;
г) а, б.
171. Разницей между генеральными и выборочными параметрами называется:
а) ошибка репрезентативности;
б) ошибка генеральной совокупности;
в) ошибка выборки;
г) а, б; д) а, в; е) б, в.
172. Какой способ отбора не дает возможность один раз отобранной единице попасть в выборку еще раз:
а) повторный;
б) бесповторный;
в) метод серий;
г) а, б.
173. Какой способ отбора дает возможность один раз отобранной единице попасть в выборку еще раз:
а) повторный;
б) бесповторный;
в) метод серий;
г) а, б.
174. Ошибка выборки зависит от:
а) ее численности;
б) вариации признака в изучаемой совокупности;
в) а, б.
175. Величины ошибок выборки:
а) прямо пропорциональны корню квадратному из численности единиц выборки;
б) обратно пропорциональны корню квадратному из численности единиц выборки;
в) прямо пропорциональны среднему квадрату отклонений единиц выборки;
г) обратно пропорциональны среднему квадрату отклонений единиц выборки;
д) а, б; е) а, в; ж) а, г; з) б, в; и) б, г; к) в, г.
176. Формула средней ошибки для бесповторной выборки имеет вид:
а)  ; б)
; б) 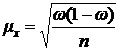 ;
;
в)  ; г)
; г)  ;
;
д) а, б; е) а, в; ж) а, г; з) б, в; и) б, г; к) в, г.
177. Формула средней ошибки для повторной выборки имеет вид:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д) а, б; е) а, в; ж) а, г; з) б, в; и) б, г; к) в, г.
178. Предельная ошибка выборки рассчитывается как:
а)  ; б)
; б)  ; в) а, б; г) нет правильного ответа.
; в) а, б; г) нет правильного ответа.
179. Численность выборки определяется как:
а)  ; б)
; б)  ; в) а, б; г) нет правильного ответа.
; в) а, б; г) нет правильного ответа.
180. При механическом способе отбора единиц в выборку:
а) отбирается каждая пятая или каждая десятая или каждая сотая и т.д. единицы;
б) генеральная совокупность предварительно разбивается на однородные группы;
в) проводится отбор не отдельных единиц, а сразу гнезд.
181. При типическом способе отбора единиц в выборку:
а) отбирается каждая пятая или каждая десятая или каждая сотая и т.д. единицы;
б) генеральная совокупность предварительно разбивается на однородные группы;
в) проводится отбор не отдельных единиц, а сразу гнезд.
182. При серийном способе отбора единиц в выборку:
а) отбирается каждая пятая или каждая десятая или каждая сотая и т.д. единицы;
б) генеральная совокупность предварительно разбивается на однородные группы;
в) проводится отбор не отдельных единиц, а сразу гнезд.
183. Дисперсия малой выборки рассчитывается как:
а)  ; б)
; б) 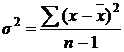 ; в)
; в)  .
.
184. Корреляционная (схоластическая) связь, это:
а) неполная связь между признаками, которая проявляется при большом числе наблюдений;
б) полная связь между признаками;
в) а, б
185. Функциональная связь, это:
а) неполная связь между признаками, которая проявляется при большом числе наблюдений;
б) полная связь между признаками;
в) а, б
186. Корреляционная таблица, это:
а) таблица, в которой записываются частоты сочетаний двух взаимосвязанных величин;
б) таблица, в которой записываются исходные данные двух взаимосвязанных величин;
в) таблица, в которой записываются результаты корреляционно-регрессионного анализа;
г) а, б.
187. Корреляционное поле показывает:
а) наличие зависимости между признаками;
б) характер зависимости между признаками;
в) а, б.
188. Факторный показатель:
а) зависимая величина;
б) независимая величина;
в) зависит от вида модели.
189. Частный коэффициент линейной корреляции может принимать значения:
а) от 0 до 1;
б) от –1 до 1;
в) может принимать любое значение.
190. Коэффициент линейной корреляции рассчитывается как:
а)  ; б)
; б)  ; в) а, б.
; в) а, б.
191. Коэффициент регрессии может принимать значения:
а) от 0 до 1;
б) от –1 до 1;
в) может принимать любое значение.
192. Надежность параметров корреляции проверяют:
а) сравнивая оцениваемую величину со средней случайной ошибкой;
б) при помощи критерия Стьюдента;
в) по средней случайной ошибке коэффициента корреляции;
г) а, б; д) а, в; е) а, б, в.
193. Для функции  критерий Стьюдента для коэффициента регрессии рассчитывается как:
критерий Стьюдента для коэффициента регрессии рассчитывается как:
а)  ;
;
б) 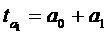 ;
;
в)  ,
,
где  – критерий Стьюдента для коэффициента регрессии.
– критерий Стьюдента для коэффициента регрессии.
194. Для функции  критерий Стьюдента для коэффициента корреляции рассчитывается как:
критерий Стьюдента для коэффициента корреляции рассчитывается как:
а)  ;
;
б)  ;
;
в)  ,
,
где  – критерий Стьюдента для коэффициента регрессии.
– критерий Стьюдента для коэффициента регрессии.
195. Коэффициент парной линейной регрессии признается статистически значимым, если фактическое значение критерия Стьюдента по сравнению с табличным;
а) меньше;
б) равное;
в) больше.
196. Для функции  критерий Фишера рассчитывается как:
критерий Фишера рассчитывается как:
а)  ; б)
; б)  ; в) а, б.
; в) а, б.
197. Функция регрессии признается статистически значимой, если фактический критерий Фишера по сравнению с табличным;
а) меньше;
б) равно;
в) больше.
198. Факторы, включаемые в модель множественной регрессии, не должны быть;
а) интеркоррелированны;
б) коллинеарные;
в) а, б.
199. Факторы, включаемые в модель множественной регрессии, являются интеркоррелированны, если;
а) теснота связи между какими-то факторами меньше, чем теснота связи между данными факторами и результативным признаком (например,  );
);
б) теснота связи между какими-то факторами больше, чем теснота связи между данными факторами и результативным признаком (например,  );
);
в) теснота связи между какими-то факторами такая же, как и теснота связи между данными факторами и результативным признаком (например,  ).
).
200. Множественный коэффициент линейной корреляции характеризует тесноту связи между:
а) результативным признаком и одним факторным признаком;
б) результативным признаком и несколькими факторными признаками;
в) факторным признаком и несколькими результативными.
201. Множественный коэффициент линейной корреляции может принимать значения:
а) от –1 до 1; б) от 0 до 1;
в) любые.
202. Множественный коэффициент линейной корреляции рассчитывается как:
а)  ; б)
; б)  ; в)
; в)  .
.
203. Множественный коэффициент детерминации показывает:
а) на сколько единиц каждый объект совокупности отличается от множественного коэффициента корреляции;
б) часть вариации результативного признака, объясненную всеми включенными в модель факторами;
в) часть вариации факторного признака, объясненную всеми включенными в модель результатами;
г) а, в.
204. Скорректированный индекс множественной детерминации рассчитывается как:
а) 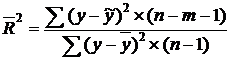 ;
;
б)  ;
;
в)  .
.
205. Коэффициент линейной регрессии показывает:
а) на сколько единиц, в натуральном выражении, изменится результативный признак, если факторный признак изменится на одну единицу;
б) на сколько процентов изменится результативный признак, если факторный признак изменится на один процент;
в) на сколько средних квадратических отклонений изменится результативный признак, если факторный признак изменится на одно среднее квадратическое отклонение.
206. Коэффициент эластичности показывает;
а) на сколько единиц, в натуральном выражении, изменится результативный признак, если факторный признак изменится на одну единицу;
б) на сколько процентов изменится результативный признак, если факторный признак изменится на один процент;
в) на сколько средних квадратических отклонений изменится результативный признак, если факторный признак изменится на одно среднее квадратическое отклонение.
207. β-коэффициент показывает:
а) на сколько единиц, в натуральном выражении, изменится результативный признак, если факторный признак изменится на одну единицу;
б) на сколько процентов изменится результативный признак, если факторный признак изменится на один процент;
в) на сколько средних квадратических отклонений изменится результативный признак, если факторный признак изменится на одно среднее квадратическое отклонение.
208. Коэффициент регрессии рассчитывается как:
а)  ; б)
; б)  ; в)
; в)  .
.
209. Коэффициент эластичности рассчитывается как:
а)  ; б)
; б)  ; в) нет верного ответа.
; в) нет верного ответа.
210. β-коэффициент рассчитывается как:
а)  ; б)
; б)  ; в) нет верного ответа.
; в) нет верного ответа.
Ответы на вопросы к тестам
Таблица 61
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| От. | г | а | б | б | г | д | а | в | б | б | а | б | б | а | ж |
| № | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| От. | в | в | а | б | а | в | а | а | б | в | в | б | е | а | б |
| № | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
| От. | в | а | а | а | б | б | а | в | г | в | а | б | а | б | в |
| № | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| От. | г | д | б | д | а | е | д | б | б | а | д | е | д | а | б |
| № | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| От. | в | г | а | з | а | б | в | г | а | б | в | б | а | г | б |
| № | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| От. | а | д | г | б | г | а | в | а | б | в | е | б | д | а | а |
| № | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 |
| От. | а | б | г | б | а | в | а | б | д | б | а | в | б | а | е |
| № | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| От. | в | а | б | в | б | з | е | в | ж | д | в | а | б | а | д |
| № | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 |
| От. | в | а | б | а | ж | а | в | б | б | а | б | а | в | б | г |
| № | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| От. | д | е | ж | з | б | а | в | г | д | е | г | б | а | д | в |
| № | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 |
| От. | г | а | е | б | б | е | д | г | а | в | б | б | а | д | а |
| № | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 |
| От. | а | а | б | а | в | д | б | а | в | з | к | д | б | в | а |
| № | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 |
| От. | б | в | б | а | б | а | в | б | б | в | в | а | в | в | в |
| № | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 |
| От. | в | в | в | б | б | б | в | б | в | а | б | в | а | б | а |
Приложения
Приложение 1
Титульный лист контрольной работы
(рекомендуемое)
Министерство сельского хозяйства Российской Федерации
Департамент научно-технологической политики и образования
Федеральное государственное образовательное учреждение
высшего профессионального образования
«Красноярский государственный аграрный университет»
Институт Экономики и финансов АПК
Кафедра__________________________
__________________________________
_____________________________________________
(наименование дисциплины)
КОНТРОЛЬНАЯ РАБОТА
____________________________________________________________
(вариант)
00.00.00.00.ПЗ[2]
(обозначение документа)
| Выполнил (Студент группы, отделения, шифр специальности) | (ФИО) | |
| (подпись) | ||
| Принял (Ученое звание, степень, или должность) | (ФИО) | |
| (подпись) |
Красноярск 20___ г
Приложение 2
Значение критерия t Стьюдента при уровне значимости 0,10, 0,05 и 0,01
| n | a
| n | a
| ||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | ||
| 1 | 6,3138 | 12,706 | 63,657 | 18 | 1,7341 | 2,1009 | 2,8784 |
| 2 | 2,9200 | 4,3027 | 9,9248 | 19 | 1,7291 | 2.0930 | 2,8609 |
| 3 | 2,3534 | 3,1825 | 5,8409 | 20 | 1,7247 | 2,0860 | 2,8453 |
| 4 | 2,1318 | 2,7764 | 4,6041 | 21 | 1,7207 | 2,0796 | 2,8314 |
| 5 | 2,0150 | 2,5706 | 4,0321 | 22 | 1,7171 | 2,0739 | 2,8188 |
| 6 | 1,9432 | 2,4469 | 3,7074 | 23 | 1,7139 | 2,0687 | 2,8073 |
| 7 | 1,8946 | 2,3646 | 3,4995 | 24 | 1,7109 | 2,0639 | 2,7969 |
| 8 | 1,8595 | 2.3060 | 3,3554 | 25 | 1,7081 | 2,0595 | 2,7874 |
| 9 | 1,8331 | 2,2622 | 3,2498 | 26 | 1,7056 | 2,0555 | 2,7787 |
| 10 | 1,8125 | 2,2281 | 3,1693 | 27 | 1,7033 | 2,0518 | 2,7707 |
| 11 | 1,7959 | 2,2010 | 3,1058 | 28 | 1,7011 | 2,0484 | 2,7633 |
| 12 | 1,7823 | 2,1788 | 3,0545 | 29 | 1,6991 | 2,0452 | 2,7564 |
| 13 | 1,7709 | 2,1604 | 3,0123 | 30 | 1,6973 | 2,0423 | 2,7500 |
| 14 | 1,7613 | 2,1448 | 2,9768 | 40 | 1,6839 | 2,0211 | 2,7045 |
| 15 | 1,7530 | 2,1315 | 2.9467 | 60 | 1,6707 | 2,0003 | 2,6603 |
| 16 | 1.7459 | 2,1199 | 2,9208 | 120 | 1.6577 | 1,9799 | 2,6174 |
| 17 | 1,7396 | 2,1098 | 2,8982 | 1,6449 | 1,9600 | 2,5758 | |
Приложение 3
Таблица 5%-го уровня распределения F (уровень значимости 0,05)
v1 – число степеней свободы для большей дисперсии;
v2 – число степеней свободы для меньшей дисперсии.
| v2 | v2 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 |
| 3 | 10,13 | 9,55 | 9,28 | 9,19 | 9,01 | 8,94 | 8,88 | 8,84 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 |
| 13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,70 | 2,64 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,62 | 2,55 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,58 | 2,51 |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,55 | 2,48 |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,52 | 2,45 |
| 21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,49 | 2,42 |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,47 | 2,40 |
| 23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,45 | 2,38 |
| 24 | 4,26 | 2,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,43 | 2,36 |
| 25 | 4,24 | 3,88 | 2,99 | 2,76 | 2,60 | 2,49 | 2,41 | 2,34 |
| 26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,39 | 2,32 |
| 27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,37 | 2,30 |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,36 | 2,29 |
| 29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,35 | 2,28 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,34 | 2,27 |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,25 | 2,18 |
| 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,20 | 2,13 |
| 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,17 | 2,10 |
| 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,10 | 2,03 |
| ∞ | 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 2,01 | 1,94 |
Окончание прил. 3
Таблица 5%-ного уровня распределения F (уровень значимости 0,05)
v1 – число степеней свободы для большей дисперсии
v2 – число степеней свободы для меньшей дисперсии
| v2 | v1 | ||||||||
| 9 | 10 | 11 | 12 | 14 | 16 | 20 | 30 | ∞ | |
| 1 | 241 | 242 | 243 | 244 | 245 | 246 | 248 | 250 | 254 |
| 2 | 19,38 | 19,39 | 19,40 | 19,41 | 19,42 | 19,43 | 19,44 | 19,46 | 19,50 |
| 3 | 8,81 | 8,78 | 8,76 | 8,74 | 8,71 | 8,69 | 8,66 | 8,62 | 8,53 |
| 4 | 6,00 | 5,96 | 5,93 | 5,91 | 5,87 | 5,84 | 5,80 | 5,74 | 5,63 |
| 5 | 4,78 | 4,74 | 4,70 | 4,68 | 4,64 | 4,60 | 4,56 | 4,50 | 4,36 |
| 6 | 4,10 | 4,06 | 4,03 | 4,00 | 3,96 | 3,92 | 3,87 | 3,81 | 3,67 |
| 7 | 3,68 | 3,63 | 3,60 | 3,57 | 3,52 | 3,49 | 3,44 | 3,38 | 3,23 |
| 8 | 3,39 | 3,34 | 3,31 | 3,28 | 3,23 | 3,20 | 3,15 | 3,08 | 2,93 |
| 9 | 3,18 | 3,13 | 3,10 | 3,07 | 3,02 | 2,98 | 2,93 | 2,86 | 2,71 |
| 10 | 3,02 | 2,97 | 2,94 | 2,91 | 2,86 | 2,82 | 2,77 | 2,70 | 2,54 |
| 11 | 2,90 | 2,86 | 2,82 | 2,79 | 2,74 | 2,70 | 2,65 | 2,57 | 2,40 |
| 12 | 2,80 | 2,76 | 2,72 | 2,69 | 2,64 | 2,60 | 2,54 | 2,46 | 2,30 |
| 13 | 2,72 | 2,67 | 2,63 | 2,60 | 2,55 | 2,51 | 2,46 | 2,38 | 2,21 |
| 14 | 2,65 | 2,60 | 2,56 | 2,53 | 2,48 | 2,44 | 2,39 | 2,31 | 2,13 |
| 15 | 2,59 | 2,55 | 2,51 | 2,48 | 2,43 | 2,39 | 2,33 | 2,25 | 2,07 |
| 16 | 2,54 | 2,49 | 2,45 | 2,42 | 2,37 | 2,33 | 2,28 | 2,20 | 2,01 |
| 17 | 2,50 | 2,45 | 2,41 | 2,38 | 2,33 | 2,29 | 2,23 | 2,15 | 1,96 |
| 18 | 2,46 | 2,41 | 2,37 | 2,34 | 2,29 | 2,25 | 2,19 | 2,11 | 1,92 |
| 19 | 2,43 | 2,38 | 2,34 | 2,31 | 2,26 | 2,21 | 2,15 | 2,07 | 1,88 |
| 20 | 2,40 | 2,35 | 2,31 | 2,28 | 2,23 | 2,18 | 2,12 | 2,04 | 1,84 |
| 21 | 2,37 | 2,32 | 2,28 | 2,25 | 2,20 | 2,15 | 2,09 | 2,00 | 1,81 |
| 22 | 2,35 | 2,30 | 2,26 | 2,23 | 2,18 | 2,13 | 2,07 | 1,98 | 1,78 |
| 23 | 2,32 | 2,28 | 2,24 | 2,20 | 2,14 | 2,10 | 2,04 | 1,96 | 1,76 |
| 24 | 2,30 | 2,26 | 2,22 | 2,18 | 2,13 | 2,09 | 2,02 | 1,94 | 1,73 |
| 25 | 2,26 | 2,24 | 2,20 | 2,16 | 2,11 | 2,06 | 2,00 | 1,92 | 1,71 |
| 26 | 2,27 | 2,22 | 2,18 | 2,15 | 2,10 | 2,05 | 1,99 | 1,90 | 1,69 |
| 27 | 2,25 | 2,20 | 2,16 | 2,13 | 2,08 | 2,03 | 1,97 | 1,88 | 1,67 |
| 28 | 2,24 | 2,19 | 2,15 | 2,12 | 2,06 | 2,02 | 1,96 | 1,87 | 1,65 |
| 29 | 2,22 | 2,18 | 2,14 | 2,10 | 2,05 | 2,00 | 1,94 | 1,85 | 1,64 |
| 30 | 2,21 | 2,16 | 2,12 | 2,09 | 2,04 | 1,99 | 1,93 | 1,84 | 1,62 |
| 40 | 2,12 | 2,07 | 2,04 | 2,00 | 1,95 | 1,90 | 1,84 | 1,74 | 1,51 |
| 50 | 2,07 | 0,02 | 1,98 | 1,95 | 1,90 | 1,85 | 1,78 | 1,69 | 1,44 |
| 60 | 2,04 | 1,99 | 1,95 | 1,92 | 1,86 | 1,81 | 1,75 | 1,65 | 1,39 |
| 100 | 1,97 | 1,92 | 1,88 | 1,85 | 1,79 | 1,75 | 1,68 | 1,57 | 1,28 |
| ∞ | 1,83 | 1,83 | 1,79 | 1,75 | 1,69 | 1,64 | 1,57 | 1,46 | 1,00 |
Приложение 4
Греческий алфавит
| Греческое написание | Прочтение | ||
| Заглавные | Строчные | Английское | Русское |
| A | a | alpha | альфа |
| B | b | beta | бета |
| G | g | gamma | гамма |
| D | d | delta | дельта |
| E | e | epsilon | эпсилон |
| Z | z | zeta | дзета |
| H | h | eta | эта |
| Q | q | theta | тета |
| I | i | iota | йота |
| K | k | kappa | каппа |
| L | l | lambda | ламбада |
| M | m | mu | мю |
| N | n | nu | ню |
| X | x | xi | кси |
| O | o | omicron | омикрон |
| P | p | pi | пи |
| R | r | rho | ро |
| S | s | sigma | сигма |
| T | t | tau | тау |
| U | u | upsilon | ипсилон |
| J F | j f | phi | фи |
| C | c | chi | хи |
| Y | y | psi | пси |
| W | w | omega | омега |
Список литературы
В основу работы положены следующие учебные и справочные пособия:
| 1. | Гришин, А.Ф. Статистика: учеб пособие / А.Ф. Гришин. - М.: Финансы и статистика, 2003. |
| 2. | Елисеева, И.И. Статистика: учеб / Под ред. И.И. Елисеевой. - М.: Проспект, 2003. |
| 3. | Ефимова, М.П.. Общая теория статистики: учеб пособие / М.П. Ефимова - М.: ИНФРА -М ,1998. |
| 4. | Зинченко, А.П. Практикум по общей теории статистики и сельскохозяйственной статистики / А.П. Зинченко. -М.: Финансы и статистика, 1988. |
| 5. | Кильдишев, Г.С. Общая теория статистики / Г.С. Кильдишев. - М.: Статистика, 1980. |
| 6. | Кимбл, Г.Как правильно пользоваться статистикой / Г. Кимбл.- М.: Финансы и статистика, 2001. |
| 7. | Пасхавер, И.С. Общая теория статистики / И.С. Пасхавер. - М.: Финансы и статистика, 1983. |
| 8. | Харченко, Л.П. Статистика. Курс лекций / Л.П. Харченко. - Новосибирск: ИНФРА-М, 1997. |
| 9. | Шмойлова, Р.А. Практикум по статистики / Р.А. Шмойлова –М.: Финансы и статистика, 2002. |
| 10. | Шмойлова, Р.А. Теория статистики / Р.А. Шмойлова -М.: Финансы и статистика, 2003. |
| 11. | Юзбашев, М.М. Общая теория статистики / М.М. Юзбашев. - М.: Финансы и статистика, 2002. |
| 12. | Копыл, В.И. Курсовая работа на компьютере / В.И. Копыл - Минск: Харвест, 2003. –48 с. |
| 13. | Статистический словарь - М.: Статистика, 1965. |
| 14. | Ряузов, Н.Н. Общая теория статистики / Н.Н. Ряузов - М.: Статистика, 1979. |
[1] также используют и другие линеаризуемте функции для построения уравнения множественной регрессии – экспоненту, гиперболу и т.д.
[2] Код обозначения документа необходимо уточнять на кафедре
Дата добавления: 2018-02-15; просмотров: 476; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
