Анализ сезонных колебаний ряда динамик
При анализе динамических рядов может быть обнаружена периодичность колебаний уровней динамического ряда, то есть наблюдается устойчивое отклонение уровней от тенденции в зависимости от периода времени (внутригодичного, внутриквартального, внутримесячного и т.д.). в данном случае статистика говорит, что в динамическом ряду наблюдаются сезонные колебания.
Сезонные колебания – внутригодичные (внутриквартальные, внутримесячные и т.д.) изменения в ряду динамики, вызванные специфическими условиями, возникающими в определенном периоде года (квартала, месяца, и т.д.). Например, в сезонность наблюдается по уровню удоев, яйценоскости, потребление топлива, сезонность наблюдается в потреблении определенных товаров и т.д.
Изучения явления сезонности имеет большое практическое значения для минимизации отрицательного воздействия сезонности на уровень развития производства, торговли и т.д. Наиболее часто, сезонные колебания статистика изучает при помощи следующих методов:
1. метод абсолютных разностей и относительных разностей
2. расчет индексов сезонности
Метод абсолютных и относительных разностей.
При методе абсолютных разностей используют непосредственно размеры данных разностей. При методе относительных разностей определяют отношения абсолютных размеров указанных разностей к среднему уровню. При расчете абсолютных и относительных разностей:
|
|
|
1. определяют абсолютные уровни ряда
2. рассчитывают средний месячный уровень ряда
3. сопоставляя абсолютные уровни ряда (находя разности или отношения) определяют показатели сезонности (абсолютные или относительные).
Расчет индексов сезонности.
Индекс сезонности показывает, во сколько раз фактический уровень динамического ряда  на определенный момент времени
на определенный момент времени  больше среднего уровня
больше среднего уровня  либо выровненного, методом скользящей средней, либо методом аналитического выравнивания, уровня. При анализе сезонных колебаний динамического ряда рассматривают развития по месяцам (кварталам, неделям, и т.д.) одного или нескольких лет (кварталов, месяцев и т.д.). Метод определения индекса сезонности зависит от того, наблюдается наличие тренда в изучаемом ряду или тренд отсутствует.
либо выровненного, методом скользящей средней, либо методом аналитического выравнивания, уровня. При анализе сезонных колебаний динамического ряда рассматривают развития по месяцам (кварталам, неделям, и т.д.) одного или нескольких лет (кварталов, месяцев и т.д.). Метод определения индекса сезонности зависит от того, наблюдается наличие тренда в изучаемом ряду или тренд отсутствует.
Если тренд отсутствует, то
· для каждого конкретного месяца (квартала, недели и т.д.):
 , (7.49)
, (7.49)
где 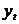 - уровень динамического ряда за месяц (квартал, неделю и т.д.)
- уровень динамического ряда за месяц (квартал, неделю и т.д.)
 - средний уровень за весь период (год, квартал и т.д.)
- средний уровень за весь период (год, квартал и т.д.)
· для больших (средних) промежутков времени (за несколько месяцев, кварталов и т.д.)
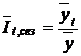 или
или 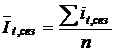 , (7.50)
, (7.50)
|
|
|
где  - средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)
- средний уровень динамического ряда за одноименные месяцы (кварталы, недели и т.д.)
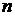 - число периодов.
- число периодов.
2. Если в динамическом ряду существует ярко выраженный тренд, расчет проводится следующим образом
а) для каждого уровня определяют значения выровненного уровня
б) рассчитывают, как отношение фактического уровня динамического ряда к выровненному уровню по тренду либо как отношение средней из фактических уровней одноименных месяцев (кварталов, недель и т.д.) к средней из выровненных данных по тем же месяцам (кварталам, неделям и т.д.).
 либо
либо 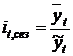 , (7.51)
, (7.51)
в) также находят среднее из отношений фактических уровней к выровненному уровню для одноименных месяцев (кварталов, недель и т.д.)
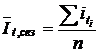 , (7.52)
, (7.52)
где 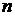 - число периодов
- число периодов
Пример 10.По хозяйству имеются данные о средней урожайности за ряд лет (табл. 20).
Таблица 20
| Год | Урожайность
| Год | Урожайность
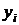
|
| 1997 | 19 | 2002 | 20 |
| 1998 | 17 | 2003 | 21 |
| 1999 | 18 | 2004 | 16 |
| 2000 | 20 | 2005 | 17 |
| 2001 | 21 | 2006 | 20 |
Рассчитать:
1. Показатели динамики:
· абсолютный прирост (цепной и базисный);
· темп роста (цепной и базисный);
|
|
|
· темп прироста (цепной);
· абсолютное значение 1% прироста;
· средние показатели динамики.
Решение.
1.Рассчитаем показатели динамики, результаты занесем в табл.21.
По полученным результатам рассчитаем средние показатели динамики.
Средний абсолютный прирост рассчитывается как:
 .
.
где 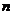 - количество абсолютных приростов.
- количество абсолютных приростов.
Таблица 21
| Год | Урожайность
| Абсолютный прирост | Темп прироста | Темп прироста | Абсолютное значение 1% прироста | ||
| цепной | базисный | цепной | базисный | цепной | цепного | ||

| 
| 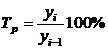
| 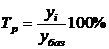
| 
| 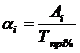
| ||
| 1997 | 19 | - | - | - | - | - | - |
| 1998 | 17 | -2 | -2 | 89,47 | 89,47 | -10,53 | 0,19 |
| 1999 | 18 | 1 | -1 | 105,88 | 94,74 | 5,88 | 0,17 |
| 2000 | 20 | 2 | 1 | 111,11 | 105,26 | 11,11 | 0,18 |
| 2001 | 21 | 1 | 2 | 105,00 | 110,53 | 5,00 | 0,20 |
| 2002 | 20 | -1 | 1 | 95,24 | 105,26 | -4,76 | 0,21 |
| 2003 | 21 | 1 | 2 | 105,00 | 110,53 | 5,00 | 0,20 |
| 2004 | 16 | -5 | -3 | 76,19 | 84,21 | -23,81 | 0,21 |
| 2005 | 17 | 1 | -2 | 106,25 | 89,47 | 6,25 | 0,16 |
| 2006 | 20 | 3 | 1 | 117,65 | 105,26 | 17,65 | 0,17 |
Средний коэффициент роста рассчитывается как:

 – число коэффициентов роста.
– число коэффициентов роста.
Средний темп роста рассчитывается как:
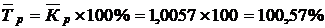
Средний темп прироста рассчитывается как:

Среднее абсолютное значение 1% среднего прироста рассчитывается как:

Пример 11.По хозяйству имеются данные о средней урожайности за ряд лет (табл. 22).
|
|
|
Таблица 22
| Год | Урожайность
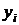
|
| 1998 | 16 |
| 1999 | 18 |
| 2000 | 20 |
| 2001 | 21 |
| 2002 | 20 |
| 2003 | 21 |
| 2004 | 23 |
| 2005 | 27 |
| 2006 | 20 |
Необходимо:
1. Провести выравнивание динамического ряда.
а) методом средних скользящих;
б) аналитическое выравнивание по линейной функции, и по функции параболы второго порядка.
2. Провести экстраполяцию на 2007год.
Решение.
1. Проведем выравнивание динамического ряда.
а) Метод средних скользящих. Для выравнивания динамического ряда методом средних скользящих рассчитаем средние уровни за определенное количество лет (в нашем случае возьмем три года) со сдвигом на одну дату.
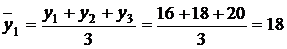
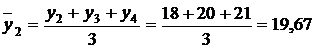
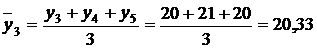
И т.д. результаты занесем в табл. 23.
б) Аналитическое выравнивание динамического ряда по прямой. Линейная функция динамического ряда имеет вид:

Рассчитаем неизвестные параметры уравнения  и
и  при помощи системы уравнений:
при помощи системы уравнений:

Назначим точку отсчета, при которой сумма показателей времени исследуемого динамического ряда будет равна нулю (  ) (табл.23).
) (табл.23).
Сократим систему уравнений:

отсюда
 и
и 
В таблице 23 рассчитаем все необходимые значения для определения параметров уравнения.
Таблица 23.
| Год | 
| Средняя скользящая

| 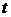
| 
| 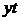
| 
|
| 1998 | 16 | -4 | 16 | -64 | 16,465 | |
| 1999 | 18 | 18,00 | -3 | 9 | -54 | 17,682 |
| 2000 | 20 | 19,67 | -2 | 4 | -40 | 18,899 |
| 2001 | 21 | 20,33 | -1 | 1 | -21 | 20,116 |
| 2002 | 20 | 20,67 | 0 | 0 | 0 | 21,333 |
| 2003 | 21 | 21,33 | 1 | 1 | 21 | 22,550 |
| 2004 | 23 | 23,67 | 2 | 4 | 46 | 23,767 |
| 2005 | 27 | 25,33 | 3 | 9 | 81 | 24,984 |
| 2006 | 26 | 4 | 16 | 104 | 26,201 | |
| Итого | 192 | 0 | 60 | 73 |
Рассчитаем:


Подставим полученные значение в уравнение:

Подставляя в полученные уравнения значения 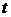 рассчитаем теоретические значения
рассчитаем теоретические значения  :
:


И т.д. результаты занесем в таблицу 22.
2. Проведем экстраполяцию на 2007год. Номер t для 2007г. будет 5. Подставим данные номера в уравнение линейного тренда и проведем прогнозирование на данный период.
Для 2007г: 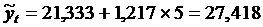
Пример 12.По хозяйству имеются данные о среднедневном надое (кг.) за ряд лет (табл. 24).
Таблица 24
| Год | Среднедневной надой
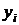
|
| 1998 | 7 |
| 1999 | 8 |
| 2000 | 11 |
| 2001 | 10 |
| 2002 | 12 |
| 2003 | 14 |
| 2004 | 10 |
| 2005 | 13 |
| 2006 | 11 |
Провести выравнивание динамического ряда по параболе второго порядка.
Решение.
Аналитическое уравнение параболы второго порядка имеет вид: 
Для расчета параметров уравнения используем систему уравнений:
 .
.
Приравняв  система сократится:
система сократится:

Рассчитаем все возможные значения в табл. 25
Таблица 25.
| Год | надой | 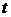
| 
| 
|
| 
| 
|
| 1998 | 7 | -4 | 16 | 256 | -28 | 112 | 6,80 |
| 1999 | 8 | -3 | 9 | 81 | -24 | 72 | 8,60 |
| 2000 | 11 | -2 | 4 | 16 | -22 | 44 | 10,04 |
| 2001 | 10 | -1 | 1 | 1 | -10 | 10 | 11,13 |
| 2002 | 12 | 0 | 0 | 0 | 0 | 0 | 11,86 |
| 2003 | 14 | 1 | 1 | 1 | 14 | 14 | 12,23 |
| 2004 | 10 | 2 | 4 | 16 | 20 | 40 | 12,24 |
| 2005 | 13 | 3 | 9 | 81 | 39 | 117 | 11,90 |
| 2006 | 11 | 4 | 16 | 256 | 44 | 176 | 11,20 |
| Итого | 96 | 0 | 60 | 708 | 33 | 585 |
Из уравнения (5) рассчитаем:

Останется система из двух уравнений:
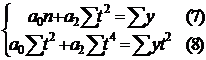 подставим значения
подставим значения 
Рассчитаем параметр  , исключив из системы параметр
, исключив из системы параметр 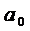 , для этого:
, для этого:
а) разделим 7-е и 8-е уравнения на коэффициенты, стоящие при  , т.е. 7-е на 9, а 8-е на 60.
, т.е. 7-е на 9, а 8-е на 60.

Таким образом, коэффициенты, стоящие при  , будут равны единице.
, будут равны единице.
б) далее из 8-го сокращенного уравнения вычтем 7-е сокращенное уравнение, исключив таким образом  .
.
Получится уравнение с одним неизвестным 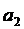 :
:


Подставим параметры  и
и  в 1-е уравнение и рассчитаем параметр
в 1-е уравнение и рассчитаем параметр  .
.


Подставим значение параметров в уравнение  :
:

Подставляя значение 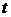 и
и  рассчитаем значения
рассчитаем значения  .
.
Пример 13. За ряд лет по хозяйству имеются данные о сдельной среднемесячной заработной плате (табл.26).
Таблица 26.
| Месяц | Год | ||
| 2004г | 2005г | 2006г | |
| Январь | 7,28 | 8,52 | 5,46 |
| Февраль | 7,54 | 9,12 | 5,88 |
| Март | 8,06 | 7,80 | 6,93 |
| Апрель | 6,76 | 7,44 | 4,62 |
| Май | 6,50 | 7,20 | 3,78 |
| Июнь | 6,11 | 6,72 | 3,99 |
| Июль | 4,16 | 6,12 | 3,32 |
| Август | 6,50 | 7,68 | 6,72 |
| Сентябрь | 8,19 | 7,80 | 6,72 |
| Октябрь | 8,97 | 7,80 | 7,77 |
| Ноябрь | 9,10 | 8,16 | 8,19 |
| Декабрь | 10,14 | 8,28 | 9,87 |
Необходимо выявить сезонность изменений среднемесячной оплаты труда, предварительно проведя аналитическое выравнивание динамического ряда по прямой или по другой более подходящей функции.
Решение. Проведем выравнивание динамического ряда по прямой 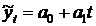 (табл. 27).
(табл. 27).
Рассчитаем параметры уравнения (см. пример 11).
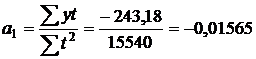


Таблица 27.
| Месяц | 
| 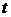
| 
| 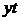
| 
|
| А | 1 | 2 | 3 | 4 | 5 |
| Январь | 7,28 | -35 | 1225 | -254,80 | 7,63 |
| Февраль | 7,54 | -33 | 1089 | -248,82 | 7,60 |
| Март | 8,06 | -31 | 961 | -249,86 | 7,57 |
| Апрель | 6,76 | -29 | 841 | -196,04 | 7,54 |
| Май | 6,50 | -27 | 729 | -175,50 | 7,51 |
| Июнь | 6,11 | -25 | 625 | -152,75 | 7,48 |
| Июль | 4,16 | -23 | 529 | -95,68 | 7,45 |
| Август | 6,50 | -21 | 441 | -136,50 | 7,42 |
| Сентябрь | 8,19 | -19 | 361 | -155,61 | 7,39 |
| Октябрь | 8,97 | -17 | 289 | -152,49 | 7,35 |
| Ноябрь | 9,10 | -15 | 225 | -136,50 | 7,32 |
| Декабрь | 10,14 | -13 | 169 | -131,82 | 7,29 |
| Январь | 8,52 | -11 | 121 | -93,72 | 7,26 |
| Февраль | 9,12 | -9 | 81 | -82,08 | 7,23 |
| Март | 7,80 | -7 | 49 | -54,60 | 7,20 |
| Апрель | 7,44 | -5 | 25 | -37,20 | 7,17 |
| Май | 7,20 | -3 | 9 | -21,60 | 7,14 |
| Июнь | 6,72 | -1 | 1 | -6,72 | 7,10 |
| Июль | 6,12 | 1 | 1 | 6,12 | 7,07 |
| Август | 7,68 | 3 | 9 | 23,04 | 7,04 |
| Сентябрь | 7,80 | 5 | 25 | 39,00 | 7,01 |
| Октябрь | 7,80 | 7 | 49 | 54,60 | 6,98 |
| Ноябрь | 8,16 | 9 | 81 | 73,44 | 6,95 |
| Декабрь | 8,28 | 11 | 121 | 91,08 | 6,92 |
| Январь | 5,46 | 13 | 169 | 70,98 | 6,89 |
| Февраль | 5,88 | 15 | 225 | 88,20 | 6,85 |
| Март | 6,93 | 17 | 289 | 117,81 | 6,82 |
| Апрель | 4,62 | 19 | 361 | 87,78 | 6,79 |
| Май | 3,78 | 21 | 441 | 79,38 | 6,76 |
| Июнь | 3,99 | 23 | 529 | 91,77 | 6,73 |
| Июль | 3,32 | 25 | 625 | 83,00 | 6,70 |
| Август | 6,72 | 27 | 729 | 181,44 | 6,67 |
| Сентябрь | 6,72 | 29 | 841 | 194,88 | 6,64 |
| Октябрь | 7,77 | 31 | 961 | 240,87 | 6,61 |
| Ноябрь | 8,19 | 33 | 1089 | 270,27 | 6,57 |
| Декабрь | 9,87 | 35 | 1225 | 345,45 | 6,54 |
| Итого | 255,20 | 0 | 15540 | -243,18 |
Подставляя значение 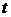 в полученное уравнение рассчитаем значения
в полученное уравнение рассчитаем значения  .
.
Рассчитаем индексы сезонности (табл.28):
Таблица 28
| Месяц | 
| 
| Индексы сезонности

|
| Январь | 7,28 | 7,63 | 0,9535 |
| Февраль | 7,54 | 7,60 | 0,9916 |
| Март | 8,06 | 7,57 | 1,0644 |
| Апрель | 6,76 | 7,54 | 0,8964 |
| Май | 6,50 | 7,51 | 0,8655 |
| Июнь | 6,11 | 7,48 | 0,8170 |
| Июль | 4,16 | 7,45 | 0,5586 |
| Август | 6,50 | 7,42 | 0,8764 |
| Сентябрь | 8,19 | 7,39 | 1,1090 |
| Октябрь | 8,97 | 7,35 | 1,2197 |
| Ноябрь | 9,10 | 7,32 | 1,2427 |
| Декабрь | 10,14 | 7,29 | 1,3906 |
| Январь | 8,52 | 7,26 | 1,1735 |
| Февраль | 9,12 | 7,23 | 1,2615 |
| Март | 7,80 | 7,20 | 1,0836 |
| Апрель | 7,44 | 7,17 | 1,0381 |
| Май | 7,20 | 7,14 | 1,0090 |
| Июнь | 6,72 | 7,10 | 0,9459 |
| Июль | 6,12 | 7,07 | 0,8652 |
| Август | 7,68 | 7,04 | 1,0906 |
| Сентябрь | 7,80 | 7,01 | 1,1126 |
| Октябрь | 7,80 | 6,98 | 1,1175 |
| Ноябрь | 8,16 | 6,95 | 1,1744 |
| Декабрь | 8,28 | 6,92 | 1,1970 |
| Январь | 5,46 | 6,89 | 0,7929 |
| Февраль | 5,88 | 6,85 | 0,8578 |
| Март | 6,93 | 6,82 | 1,0156 |
| Апрель | 4,62 | 6,79 | 0,6802 |
| Май | 3,78 | 6,76 | 0,5591 |
| Июнь | 3,99 | 6,73 | 0,5929 |
| Июль | 3,32 | 6,70 | 0,4956 |
| Август | 6,72 | 6,67 | 1,0078 |
| Сентябрь | 6,72 | 6,64 | 1,0126 |
| Октябрь | 7,77 | 6,61 | 1,1763 |
| Ноябрь | 8,19 | 6,57 | 1,2458 |
| Декабрь | 9,87 | 6,54 | 1,5085 |
| Итого | 35,999278 |
Рассчитаем средний индекс сезонности:

Большое значение индекса сезонности указывает на наличие сезонных колебаний.
Статистические индексы
Обозначения индексов. Буквой «i» обозначаются индивидуальные (частные) индексы, буквой «I» - общие индексы. Знак внизу справа означает период: 0-базисный; 1-отчетный. Помимо этого, используются определенные символы для обозначения индексируемых показателей:
q - количество (объем) какого-либо товара в натуральном выражении;
p - цена единица товара;
z - себестоимость единицы продукции;
w - выработка продукции в стоимостном выражении на одного рабочего или в единицу времени;
v - выработка продукции в натуральном выражении на одного рабочего или в единицу времени;
t – затраты рабочего времени на производство единицы продукции;
T - общие затраты времени (tq) или численность рабочих;
pq - стоимость продукции или товарооборот;
zq – издержки производства.
Индивидуальные индексы получают в результате сравнения однотоварных явлений.
Индекс физического объема продукции  рассчитывается по формуле:
рассчитывается по формуле:
 , (8.1)
, (8.1)
Индивидуальный индекс цен:
 , (8.2)
, (8.2)
Индивидуальный индекс себестоимости единицы продукции:
 , (8.3)
, (8.3)
Производительность труда может быть измерена количеством продукции, производимой в единицу времени (v), или затратами рабочего времени на производство единицы продукции (t). Поэтому можно построить:
· индекс количества продукции, произведенной в единицу времени:
 , (8.4)
, (8.4)
· индекс производительности труда по трудовым затратам:
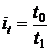 , (8.5)
, (8.5)
Так как между количеством продукции, произведенной в единицу времени, и затратами рабочего времени на производство единицы продукции существует обратно пропорциональная зависимость, т.е.  , то индекс получается в результате деления величины показателя в базисном периоде на величину в текущем периоде.
, то индекс получается в результате деления величины показателя в базисном периоде на величину в текущем периоде.
Для характеристики производительности труда часто используется индивидуальный индекс выработки продукции в стоимостном выражении на одного рабочего:
 , (8.6)
, (8.6)
где p – сопоставимые цены.
Агрегатный индекс - сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов.
Индексируемой величиной называется признак, изменение которого изучается (цена товаров, курс акций, затраты рабочего времени на производство продукции, количество проданных товаров и т.д.).
Вес индекса - это величина, служащая для целей соизмерения индексируемых величин.
При выборе веса индекса принято руководствоваться следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период, при построении индекса качественного показателя используются веса отчетного периода.
Индекс стоимости продукции или товарооборота (  ) представляет собой отношение стоимости продукции текущего периода (
) представляет собой отношение стоимости продукции текущего периода ( 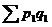 ) к стоимости продукции в базисном периоде (
) к стоимости продукции в базисном периоде (  ) и определяется по формуле:
) и определяется по формуле:
 , (8.7)
, (8.7)
Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости продукции.
Индекс физического объема продукции - это индекс количественного показателя:
 , (8.8)
, (8.8)
Индекс физического объема продукции показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объема ее производства или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения физического объема ее производства.
Индекс цен - это индекс качественного показателя:
 , (8.9)
, (8.9)
где в числителе - фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров в ценах базисного периода.
Индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за снижения цен или сколько процентов составляет рост (снижение) стоимости продукции в результате изменения цен.
Стоимость продукции можно представить как произведение количества товара на его цену. Точно такая же связь существует и между индексами стоимости, физического объема и цен, т.е.:
 или
или  , (8.10)
, (8.10)
Разность числителя и знаменателя каждого индекса-сомножителя выражает размер изменения общей абсолютной величины под влиянием изменения одного фактора. Алгебраическая сумма этих разностей равна разности числителя и знаменателя индекса стоимости продукции:
 , (8.11)
, (8.11)
Средний индекс - это индекс, вычисленный как средняя величина из индивидуальных индексов.
Средний арифметический индекс физического объема продукции вычисляется по формуле:
 , (8.12)
, (8.12)
Средний арифметический индекс производительности труда определяется следующим образом:
 , (8.13)
, (8.13)
Индексы других качественных показателей (цен, себестоимости и т.д.) определяются по формуле средней гармонической взвешенной величины.
Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса. Например, индекс себестоимости можно исчислить так:
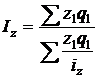 , а индекс цен:
, а индекс цен:  , (8.14)
, (8.14)
Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс переменного состава себестоимости продукции одного и того же вида рассчитывается по формуле:
 , (8.15)
, (8.15)
где 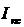 - индекс переменного состава.
- индекс переменного состава.
Индекс переменного состава отражает изменение не только индексируемой величины (в данном случае себестоимости), но и структуры совокупности (весов).
Индекс постоянного (фиксированного) состава - это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксированного состава определяется как агрегатный индекс. Так, индекс фиксированного состава себестоимости продукции рассчитывают по формуле:
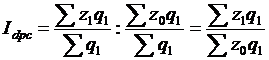 , (8.16)
, (8.16)
где  - индекс фиксированного состава.
- индекс фиксированного состава.
Под индексом структурных сдвигов понимают индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления. Индекс определяется по формуле (при изучении изменения среднего уровня себестоимости):
 , (8.17)
, (8.17)
где  - индекс структурных сдвигов.
- индекс структурных сдвигов.
Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получать другие. Так, индекс издержек производства - это произведение индекса себестоимости продукции и индекса физического объема продукции:
 , (8.18)
, (8.18)
Индекс затрат времени на производство продукции может быть получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемкости, т.е. индекс производительности труда:
 , (8.19)
, (8.19)
Индекс производительности труда рассчитывается на основе следующей формулы  , т.е. представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах.
, т.е. представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах.
Индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых):
 , (8.20)
, (8.20)
Пример 14. По хозяйству за два года имеются данные о количестве реализованной продукции растениеводства и о цене ее реализации (табл. 29, исходные данные).
Необходимо рассчитать:
1. Индивидуальные индексы физического объема и цен по каждому виду продукции.
2. Рассчитать агрегатные индексы и абсолютные приросты:
· товарооборота (стоимости);
· физического объема;
· цен.
Решение.
1. Рассчитаем индивидуальные индексы физического объема и цен рассчитываются как отношение уровня отчетного периода к базисному периоду, результаты занесем в табл. 29.
2. Рассчитаем агрегатные индексы.
Индекс товарооборота, показывает изменение стоимости проданных товаров за счет изменение физического объема реализации этого товара и за счет изменения цен:
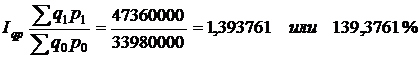
Абсолютный прирост товарооборота рассчитывается:

То есть за счет изменения физического объема реализованной продукции и цен реализации товарооборот увеличился на 39,38% или на 13380000руб.
Индекс физического объема показывает изменение стоимости проданных товаров за счет только изменения объема реализации.

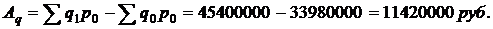
То есть за счет изменения физического объема товарооборот увеличился на 33,31% или 11420000руб.
Индекс цен показывает изменение товарооборота за счет только изменения цен.
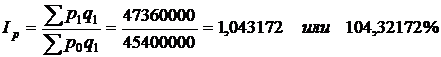

Между индексами и абсолютными приростами товарооборота физического объема и цен существует следующая взаимосвязь:

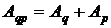
В нашем случае такое равенство соблюдается.
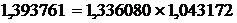

Таблица 29
|
Продукция | Исходные данные | Расчетные данные | |||||||
| Реализовано, ц | Цена реализации, руб. /ц. | Индивидуальные индексы | Выручка, руб. | ||||||
базисный период
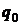
| отчетный период

| базисный период

| отчетный период

| 
| 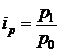
| за базисный период

| за отчетный период

| за условный период

| |
| Зерно | 80000 | 120000 | 201 | 220 | 1,5000 | 1,0945 | 16080000 | 26400000 | 24120000 |
| Картофель | 100000 | 90000 | 102 | 96 | 0,9000 | 0,9412 | 10200000 | 8640000 | 9180000 |
| Капуста | 70000 | 110000 | 110 | 112 | 1,5714 | 1,0182 | 7700000 | 12320000 | 12100000 |
| Итого | х | х | х | х | х | х | 33980000 | 47360000 | 45400000 |
Таблица 30.
|
Продукция | Исходные данные | Расчетные данные | |

| 
| условная стоимость

| |
| Зерно | 16080000 | 1,5000 | 24120000 |
| Картофель | 10200000 | 0,9000 | 9180000 |
| Капуста | 7700000 | 1,5714 | 12099780 |
| Итого | 33980000 | х | 45399780 |
Пример 15. По хозяйству за два года даны сведения о стоимости реализованной продукции растениеводства за базисный период  и величине индивидуальных индексов физического объема
и величине индивидуальных индексов физического объема 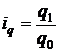 (табл. 30).
(табл. 30).
Рассчитать изменение товарооборота за счет изменения физического объема.
Решение. Изменение товарооборота за счет изменение физического объема показывает индекс физического объема, но по нашим данным рассчитать общий индекс физического объема 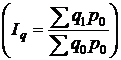 мы не можем из-за отсутствия данных о количестве проданного товара. Поэтому, учитывая наличие значений индивидуальных индексов физического объема, рассчитаем средний арифметический индекс физического объема:
мы не можем из-за отсутствия данных о количестве проданного товара. Поэтому, учитывая наличие значений индивидуальных индексов физического объема, рассчитаем средний арифметический индекс физического объема:
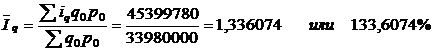
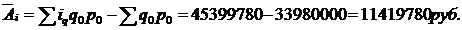
То есть, стоимость реализованной продукции за счет изменения физического объема, в среднем увеличилась на 33,6074% или на 1141978руб.
Пример 16. По хозяйству за два года даны сведения о стоимости реализованной продукции растениеводства за отчетный период  и величине индивидуальных индексов цен
и величине индивидуальных индексов цен  (табл. 31).
(табл. 31).
Таблица 31.
|
Продукция | Исходные данные | Расчетные данные | |

| 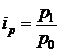
| условная стоимость

| |
| Зерно | 26400000 | 1,0945 | 24120603 |
| Картофель | 8640000 | 0,9412 | 9179770,51 |
| Капуста | 12320000 | 1,0182 | 12099783,9 |
| Итого | 47360000 | х | 45400157,5 |
Рассчитать изменение стоимости продукции за счет изменение цен.
Решение. Изменение товарооборота за счет изменение цен показывает индекс цен, но по нашим данным рассчитать общий индекс цен  мы не можем из-за отсутствия данных о ценах реализации. Поэтому, учитывая наличие значений индивидуальных индексов цен, рассчитаем средний гармонический индекс цен:
мы не можем из-за отсутствия данных о ценах реализации. Поэтому, учитывая наличие значений индивидуальных индексов цен, рассчитаем средний гармонический индекс цен:
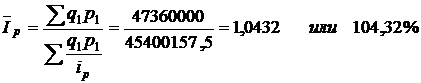
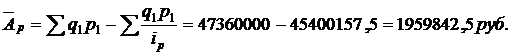
То есть товарооборот за счет изменения цен реализации в среднем увеличился на 4,32% или 1959842,5руб.
Пример 17. По хозяйству, за два года, имеются данные о количестве посевных площадей и урожайности зерновых культур (табл. 32).
Таблица 32
|
Культура | Исходные данные | Расчетные данные | |||||
| Посевная площадь, га. | Урожайность, ц/га | Валовой сбор, ц. | |||||
| базисный | отчетный | базисный | отчетный | базисный | отчетный | условный | |

| 
| 
| 
| 
| 
| 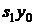
| |
| Пшеница | 9200 | 9600 | 19 | 21 | 174800 | 201600 | 182400 |
| Ячмень | 14300 | 14350 | 22 | 18 | 314600 | 258300 | 315700 |
| Овес | 5600 | 8500 | 20 | 17 | 112000 | 144500 | 170000 |
| Итого | 29100 | 32450 | х | х | 601400 | 604400 | 668100 |
Необходимо провести индексный анализ валового сбора зерновых, то есть определить изменение валового сбора за счет изменения площади посева, структуры посевов и за счет изменения урожайности.
Решение. Рассчитаем валовые сборы базисный, отчетный и условный, результаты занесем в табл. 32.
Рассчитаем индекс переменного состава валового сбора:

Между индексом валового сбора индексом посевных площадей индексом урожайности индексом посевных площадей и индексом структуры посевных площадей существует взаимосвязь.
Индекс переменного состава валового сбора можно представить как произведение двух индексов:
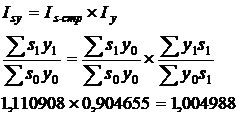
Рассчитаем
Индекс посевных площадей и структуры

Индекс урожайности

Разложим индекс посевных площадей и структуры на индекс размера посевных площадей и индекс структуры посевных площадей
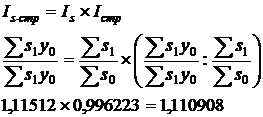
Рассчитаем:
индекс посевных площадей

индекс структуры
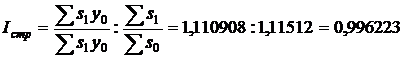
Соответственно индекс валового сбора можно представить как произведение индекс урожайности индекса посевной площади и индекса структуры посевной площади.

На основании индексного анализа валового сбора зерновых можно сказать:
· за счет изменение урожайности валовой сбор уменьшился на 9,5345%;
· за счет изменение площади посева валовой сбор увеличился на 11,512%;
· за счет изменения структуры посевных площадей валовой сбор уменьшился на 0,3777%.
Пример 18. В таблице 33 приведены сведения о количестве произведенной продукции и затратах труда на 1ц. продукции за два года.
Необходимо рассчитать трудовой и стоимостной индексы производительности труда.
Решение.
Трудовой индекс производительности труда рассчитывается как:
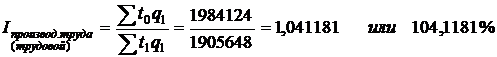

То есть, производительность труда в отчетном году по сравнению с базисным возросла на 4,1181%.
Экономия рабочего времени составила 78476 часов за счет роста производительности труда.
Таблица 33
|
| Исходные данные | Расчетные данные | ||||||||
| Количество продукции, ц. | Затраты труда на 1ц., чел.-ч. | Цена 1ц. Руб. | Затраты труда на всю продукцию, чел.-ч. | Стоимость валовой продукции, руб. | ||||||
| базисный | отчетный | базисный | отчетный | базисный | отчетный | условный | базисный | условный | ||
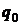
| 
| 
| 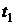
| 
| 
| 
| 
| 
| 
| |
| Зерно | 240000 | 320000 | 0,69 | 0,64 | 230 | 165600 | 204800 | 220800 | 55200000 | 73600000 |
| Привес КРС | 14120 | 12540 | 20,6 | 21,2 | 11000 | 290872 | 265848 | 258324 | 155320000 | 137940000 |
| Молоко | 330000 | 350000 | 4,3 | 4,1 | 630 | 1419000 | 1435000 | 1505000 | 207900000 | 220500000 |
| Итого | х | х | х | х | х | 1875472 | 1905648 | 1984124 | 418420000 | 432040000 |
Таблица 34
|
| Исходные данные | Расчетные данные | ||||||||
| Количество продукции, ц. | Себестоимость 1ц., руб. | Цена 1ц. Руб. | Затраты на продукцию, чел.-ч. | Стоимость валовой продукции, руб. | ||||||
| базисный | отчетный | базисный | отчетный | базисный | отчетный | условный | базисный | условный | ||
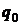
| 
| 
| 
| 
| 
| 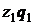
| 
| 
| 
| |
| Зерно | 240000 | 320000 | 210 | 205 | 230 | 50400000 | 65600000 | 67200000 | 55200000 | 73600000 |
| Привес КРС | 14120 | 12540 | 9800 | 10000 | 11000 | 138376000 | 125400000 | 122892000 | 155320000 | 137940000 |
| Молоко | 330000 | 350000 | 550 | 560 | 630 | 181500000 | 196000000 | 192500000 | 207900000 | 220500000 |
| Итого | х | х | х | х | х | 370276000 | 387000000 | 382592000 | 418420000 | 432040000 |
Стоимостной индекс производительности труда рассчитывается как отношение средней производительности труда базисного и отчетного годов.
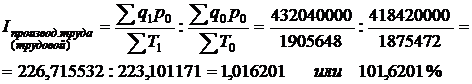
Пример 19.В таблице 34 приведены сведения о количестве произведенной продукции и себестоимости ее производства за два года.
Рассчитать среднее изменение в затратах на производство продукции.
Решение. Среднее изменение в затратах на производство продукции можно определить рассчитав индекс себестоимости и индекс средних затрат на рубль совокупной продукции.
Индекс себестоимости рассчитывается как:

Себестоимость продукции увеличилась на 1,1152% в отчетном периоде по сравнению с базисным.
Перерасход за счет увеличения себестоимости составила:

Индекс средних затрат на рубль совокупной продукции рассчитывается как:
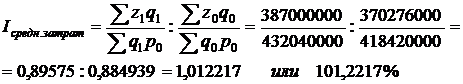
То есть в среднем затраты на рубль продукции возросли на 1,2217%.
Выборочное наблюдение
Выборочное наблюдение – несплошное наблюдение, при котором исследованию подвергается часть единиц изучаемой совокупности, отобранных в определенном порядке.
Вся совокупность, по которой проводится исследование, называется генеральной совокупностью.
Отобранные единицы генеральной совокупности для непосредственного анализа называются выборочной совокупностью (выборка).
Генеральная совокупность может быть реальной, а может быть гипотетической, включающей случаи, которые реально не существуют, например, все возможные результаты эксперимента.
В выводной статистике принято строго различать параметры и свойства генеральной совокупности и их оценки по данным выборки. С этой целью принята следующая система обозначений; генеральные параметры обозначаются греческими буквами, выборочные показатели, которые рассматриваются как оценки генеральных параметров, обозначаются латинскими буквами.
Например, табл. 35.
Таблица 35
Дата добавления: 2018-02-15; просмотров: 977; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
