Показатели вариации альтернативного признака

Альтернативный признак –это качественный (атрибутивный) признак, который показывает наличие или отсутствие данного признака у единицы совокупности (да или нет).

Среднее значение альтернативного признака:

,                           (6.39)

 

где  – доля единиц совокупности, обладающая альтернативным признаком;

 – доля единиц совокупности, не обладающая альтернативным признаком, а .

Дисперсия альтернативного признака:

 

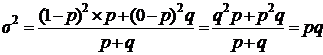,         (6.40)

Показатели вариации для сгруппированных признаков

Общая дисперсия  показывает величину вариации во всей совокупности, сложившуюся под влиянием всех факторов:

 

 – простая,                     (6.41)

 

 – взвешенная,               (6.42)

 

Внутригрупповая (случайная) дисперсия  показывает величину вариации внутри групп, на которые разбита совокупность, обусловленная случайными причинами:

 

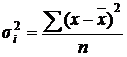 – простая,                       (6.43)

 

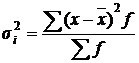 – взвешенная,               (6.44)

 

где  – групповая средняя.

По всем группам рассчитывают среднюю внутригрупповую дисперсию :

 

 – простая,                             (6.45)

 

 – взвешенная,                    (6.46)

 

где  – общая численность по всем группам;

Межгрупповая (систематическая) дисперсия  показывает величину вариации групповых средних относительно общей средней, обусловлена систематическими причинами.

 

 – простая,                    (6.47)

 

 – взвешенная,          (6.48)

 

где  – число групп.

Все три вида дисперсии связанны Законом сложения дисперсий – общая дисперсия всегда равна сумме средней внутригрупповой и межгрупповой дисперсий:

 

,                                     (6.49)

 

Для характеристики влияния группировочного признака на общую вариацию рассчитывают корреляционное отношение :

 

,                                         (6.50)

 

Чем больше корреляционное отношение, тем больше фактор, положенный в основание группировки, оказывает влияние на общую вариацию.

Моменты распределения

Моменты распределения –обобщающая характеристика, определяющая характер распределения. Данное понятие взято из механики.

Моментом -го порядка называется средняя из -х степеней отклонений переменных значений признака  от некоторой величины:

 

 – ,                          (6.51)

 

Моменты, в зависимости от величины , называют:

· начальные;

· начальные относительно ;

· центральные.

Начальные моментырассчитывают, подставляя в предыдущую формулу:

 

: ,                               (6.52)

 

В практике статистики применяют следующие начальные моменты:

 

· нулевого порядка: ,         (6.53)

 

· первого порядка: ,              (6.54)

 

· второго порядка: ,             (6.55)

 

· третьего порядка: ,           (6.56)

 

· четвертого порядка: ,       (6.57)

 

Условные моменты получают при , не равной средней арифметической и отличной от 0:

 

,                                    (6.58)

 

В практике статистики применяют следующие условные моменты:

 

· первого порядка: ,                    (6.59)

 

· второго порядка: 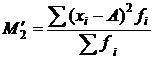,                (6.60)

 

· третьего порядка: ,                (6.61)

 

· четвертого порядка: ,            (6.62)

 

Центральные моменты получают, когда .

В практике статистики применяют следующие центральные моменты:

 

· нулевого порядка: ,                              (6.63)

 

· первого порядка: , (6.64)

 

· второго порядка: ,               (6.65)

 

· третьего порядка: ,   (6.66)

 

· четвертого порядка:

,                      (6.67)

 

На практике используются только центральные моменты третьего порядка для определения показателя асимметрии и четвертого порядка для определения показателя эксцесса.

---

Дата добавления: 2018-02-15; просмотров: 534; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!