Выделение тренда динамического ряда
После того как динамический ряд был исследован на предмет наличия в нем тренда, и данный тренд был обнаружен, приступают к непосредственному выделению тренда с экстраполяцией полученных результатов. Выравнивание динамического ряда производят с помощью механических и аналитических методов выравнивания.
Метод скользящей средней заключается в замене исходного динамического ряда новым, расчетным рядом, состоящим из средних уровней за определенный период, со сдвигом на одну дату. Если исходный динамический ряд обозначить как  , то ряд, выровненный методом скользящей средней (за трехлетний период), будет выглядеть как:
, то ряд, выровненный методом скользящей средней (за трехлетний период), будет выглядеть как:
 ;
;  ;
;  ; и т.д. (7.16)
; и т.д. (7.16)
Аналитическое выравнивание позволяет определить основную тенденцию развития явления во времени, т.е. обобщенный (суммарный), проявляющийся во времени результат действия всех факторов, влияющий на развития изучаемого явления во времени. При этом уровни ряда динамики выражаются как функции времени:
 или
или  , (7.17)
, (7.17)
где  – фактические уровни динамического ряда;
– фактические уровни динамического ряда;
 - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени  ;
;
 - отклонение от тенденции (случайное и циклическое).
- отклонение от тенденции (случайное и циклическое).
При аналитическом выравнивании чаще всего применяют следующие трендовые модели:
1. Линейная  , (7.18)
, (7.18)
|
|
|
2. Парабола второго порядка  , (7.19)
, (7.19)
3. Кубическая парабола  , (7.20)
, (7.20)
4. Показательная  , (7.21)
, (7.21)
5. Экспоненциальная  , (7.23)
, (7.23)
6. Модифицированная экспонента  , (7.24)
, (7.24)
7. Кривая Гомперца  , (7.25)
, (7.25)
8. Логистическая кривая 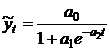 , (7.26)
, (7.26)
9. Логарифмическая парабола  , (7.27)
, (7.27)
10. Гиперболическая  , (7.28)
, (7.28)
Выбор вида модели проводят при помощи графического или экспериментального методов.
Статистическую оценку уравнения проводят при помощи критерия Фишера  . Для чего рассчитывается фактический уровень данного критерия
. Для чего рассчитывается фактический уровень данного критерия  , который сравнивается с теоретическим (табличным) значением
, который сравнивается с теоретическим (табличным) значением  при степенях свободы
при степенях свободы  ,
,  степенях свободы и уровне значимости
степенях свободы и уровне значимости  (как правила
(как правила  ).
).
 ,
,  , (7.29)
, (7.29)
где  – число параметров функции;
– число параметров функции;
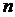 – число уровней ряда;
– число уровней ряда;
 , (7.30)
, (7.30)
 , (7.31)
, (7.31)
|
|
|
 , (7.32)
, (7.32)
Если  (приложение 3), то уравнение регрессии значимо.
(приложение 3), то уравнение регрессии значимо.
Аналитическое выравнивание по прямой
Аналитическое уравнение прямой имеет вид:
 , (7.33)
, (7.33)
Для того чтобы рассчитать  , надо найти неизвестные параметры уравнения
, надо найти неизвестные параметры уравнения 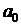 и
и  , для чего воспользуемся методом наименьших квадратов, который в данном случае даст систему из двух нормальных уравнений:
, для чего воспользуемся методом наименьших квадратов, который в данном случае даст систему из двух нормальных уравнений:
 , (7.34)
, (7.34)
Так как время - понятие относительное и зависит только от точки отсчета, можно назначить такую точку отсчета, что сумма показателей времени исследуемого динамического ряда будет равна нулю( 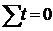 ).
).
При нечетном числе уровней изучаемого динамического ряда за точку отсчета принимают серединный уровень ряда, который обозначают как  . Периоды, стоящие выше данного уровня, обозначают отрицательными натуральными числами
. Периоды, стоящие выше данного уровня, обозначают отрицательными натуральными числами  и т.д. Уровни, стоящие ниже
и т.д. Уровни, стоящие ниже  , обозначают положительными числами
, обозначают положительными числами  и т.д. Например, ряд из семи уровней будет обозначен как
и т.д. Например, ряд из семи уровней будет обозначен как 
Если число уровней изучаемого динамического ряда четное, то точку отсчета берут между двумя серединами уровней, она не обозначается. Периоды, стоящие выше, обозначают отрицательными натуральными числами  и т.д. Уровни, стоящие ниже, обозначают положительными числами
и т.д. Уровни, стоящие ниже, обозначают положительными числами  и т.д. Например, ряд из восьми уровней будет обозначен как
и т.д. Например, ряд из восьми уровней будет обозначен как  .
.
|
|
|
Подставив 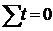 в уравнения системы, мы значительно ее упростим:
в уравнения системы, мы значительно ее упростим:
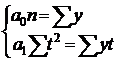 , (7.35)
, (7.35)
отсюда 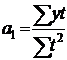 и
и  , (7.36)
, (7.36)
Для линейной зависимости параметр 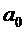 рассматривается как обобщенный начальный уровень ряда,
рассматривается как обобщенный начальный уровень ряда,  – как параметр силы связи, он показывает среднее изменение изучаемого явления за один период времени.
– как параметр силы связи, он показывает среднее изменение изучаемого явления за один период времени.
Подставив значение рассчитанных параметров уравнения  ,
,  и величину периодов времени
и величину периодов времени  , рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую прямую линию (линейный тренд). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
, рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую прямую линию (линейный тренд). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
Дата добавления: 2018-02-15; просмотров: 600; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
