Определение средней ошибки выборочного наблюдения.
Средняя ошибка при случайном повторном отборевыборочной средней рассчитывается по формуле:
, (9.4)
где 
– средняя ошибка выборочной средней;
– дисперсия выборочной совокупности;
n – численность выборки.
Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:
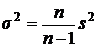, (9.5)
Если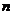 
достаточно велико, то 
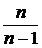близко к единице, этим сомножителем можно пренебречь и генеральную дисперсию можно заменить выборочной дисперсией.
Средняя ошибка выборочной доли при случайном повторном отборе:
, (9.6)
Средняя ошибка выборочной средней при случайном бесповторном отборе:
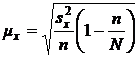, (9.7)
где 
– численность генеральной совокупности.
Средняя ошибка выборочной доли при случайном бесповторном отборе:
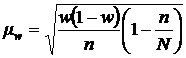, (9.8)
где 
– доля единиц, имеющих изучаемый признак;
n – численность выборки;
– численность единиц генеральной совокупности.
Определение предельной ошибки выборочного наблюдения.
Отклонение выборочной средней (доли) от генеральной средней (доли) с какой-то вероятностью 
называется предельной ошибкой выборки.
Предельная ошибка выборки 
связана со средней ошибкой выборки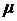 
отношением:
|
|
|
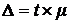, (9.9)
– коэффициент кратности ошибки (коэффициент доверия) выборки зависит от вероятности 
, с которой гарантируется, что величина предельной ошибки не превысит 
среднюю ошибку.
Таблица 36
Значение гарантированного коэффициента 
| 
|
|
|
|
|
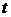
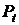
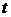
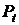
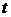
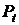
| 1,00 | 0,6827 | 1,70 | 0,9109 | 2,40 | 0,9836 |
| 1,10 | 0,7287 | 1,80 | 0,9281 | 2,50 | 0,9876 |
| 1,20 | 0,7699 | 1,90 | 0,9426 | 2,60 | 0,9907 |
| 1,30 | 0,8064 | 2,00 | 0,9545 | 2,70 | 0,9931 |
| 1,40 | 0,8385 | 2,10 | 0,9643 | 2,80 | 0,9949 |
| 1,50 | 0,8664 | 2,20 | 0,9722 | 2,90 | 0,9963 |
| 1,60 | 0,8904 | 2,30 | 0,9786 | 3,00 | 0,9973 |
При бесповторном отборе предельная ошибка для выборочной долиопределяется как:
, (9.10)
При бесповторном отборе предельная ошибка выборочной средней определяется как:
, (9.11)
При повторном отборе предельная ошибка выборочной доли определяется как:
, (9.12)
При повторном отборе предельная ошибка выборочной средней определяется как:
, (9.13)
Определение необходимой численности выборки
Необходимая численность выборки при повторном отборе для выборочной средней рассчитывается как:
|
|
|
, (9.14)
Необходимая численность выборки при повторном отборе для выборочной доли рассчитывается как:
, (9.15)
Необходимая численность выборки при бесповторном отборе рассчитывается как:
, (9.16)
Необходимая численность выборки при бесповторном отборе рассчитывается как:
, (9.17)
Малая выборка – выборка, объем которой не превышает 20 единиц.
Средняя ошибка малой выборки 
рассчитывается как:
, (9.18)
где 
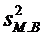– дисперсия малой выборки.
, (9.19)
Предельная ошибка малой выборки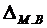 
определяется как:
(9.20)
В малых выборках коэффициент доверия 
зависит не только от заданной доверительной вероятности. Согласно распределению Стьюдента, вероятность того, что предельная ошибка не превысит 
среднюю ошибку, зависит и от величины 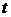, и от численности выборки n. Для отдельных значений 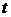и n доверительная вероятность малой выборки рассчитывается по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:
Дата добавления: 2018-02-15; просмотров: 520; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!