Аналитическое выравнивание по параболе второго порядка
Аналитическое уравнение параболы второго порядка имеет вид:
 , (7.37)
, (7.37)
Для расчета параметров уравнения используем систему уравнений:
 , (7.38)
, (7.38)
Как и в аналитическом выравнивании, приравниваем сумму показателей времени исследуемого динамического ряда к нулю(  ).
).
Система уравнений сократится:
 , (7.39)
, (7.39)
Из уравнения (5) рассчитаем:
 , (7.40)
, (7.40)
Останется система из двух уравнений:
 , (7.41)
, (7.41)
Рассчитаем параметр  , исключив из системы параметр
, исключив из системы параметр  , для этого:
, для этого:
1) разделим 7-е и 8-е уравнения на коэффициенты, стоящие при 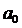 , т.е. 7-е на n, а 8-е на
, т.е. 7-е на n, а 8-е на  . Таким образом коэффициенты, стоящие при
. Таким образом коэффициенты, стоящие при  , будут равны единице.
, будут равны единице.
2) далее из 8-го сокращенного уравнения вычтем 7-е сокращенное уравнение, исключив таким образом  . Получится уравнение с одним неизвестным
. Получится уравнение с одним неизвестным 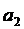 , рассчитаем его.
, рассчитаем его.
Подставим параметры  и
и  в 1-е уравнение и рассчитаем параметр
в 1-е уравнение и рассчитаем параметр  .
.
Подставив значение рассчитанных параметров уравнения  ,
,  ,
,  и величину периодов времени
и величину периодов времени  , рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую линию параболы второго порядка (тренд параболы второго порядка). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
, рассчитаем выровненные теоретические значения уровней динамического ряда, которые образуют теоретическую линию параболы второго порядка (тренд параболы второго порядка). Далее проводят оценку надежности полученного уравнения с помощью критерия Фишера (см. выше).
|
|
|
Статистический анализ случайной величины.
Выравнивание динамического ряда дает возможность определить действия факторов на изменения изучаемого явления, отраженного в динамическом ряду. После проведения выравнивания видно, что фактические уровни исходного динамического ряда отклоняются в разные стороны от уровней выровненного ряда. Данные отклонения образуют так называемый колеблющийся остаток. В статистике данный остаток случайной компонентой динамического ряда. Таким образом, мы можем разложить уровни динамического ряда на систематическую и случайную компоненты.
 , (7.42)
, (7.42)
где 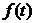 - часть уровня, выраженная трендом
- часть уровня, выраженная трендом
 - случайная компонента.
- случайная компонента.
Для анализа случайной величины в статистики изучают ее колеблемость, которая выражается колеблемостью уровней исходного динамического ряда относительно уровней выровненного динамического ряда. Мерой измерения колеблемости уровней выступают:
· дисперсия случайной величины
 , (7.43)
, (7.43)
· среднее квадратическое отклонение случайной величины
 , (7.44)
, (7.44)
· коэффициент вариации случайной величины
|
|
|
 , (7.45)
, (7.45)
Коэффициент вариации будет тем меньше, чем меньше разница между выровненными и фактическими уровнями, то есть коэффициент вариации служит критерием правильности выбора уравнения выравнивания.
На выбор аналитического уравнения тренда оказывает большое влияние показатель колеблемости уровней исходного динамического ряда. Поэтому расчет показателей колеблемости исходного динамического ряда необходимо провести предварительно, перед непосредственно аналитическим выравниванием. Для данного анализа применяют показатель Ястремского, который строится на расчете разностей первого порядка (абсолютный приростов) уровней динамического ряда и построение показателя средней величины из квадратов абсолютных приростов  :
:
 , (7.46)
, (7.46)
где,  - абсолютные приросты уровней ряда в квадрате
- абсолютные приросты уровней ряда в квадрате
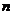 – число уровней.
– число уровней.
Ястремский доказал существование зависимости между дисперсией уровней и показателем колеблемости:
 откуда
откуда  и соответственно
и соответственно  , (7.47)
, (7.47)
Определив среднее квадратическое отклонение до того как был определен тренд, имеется возможность оценить величину колеблемости случайной компоненты (разности между уровнями исходного динамического ряда и уровнями тренда). В случае, когда колеблемость уровней ряда около тренда превосходит его общую колеблемость, тренд рассчитан не правильно, следует выбрать другую форму зависимости, что бы приблизить
|
|
|
Экстраполяция в динамике предполагает распространение полученных выводов, полученных в прошлом на будущее время. При этом предполагается, что закономерность развития динамического ряда сохраняется в будущем.
Интерполяция в динамике предполагает расчет неизвестных промежуточных значений динамического ряда.
Экстраполяция и интерполяция проводятся графическим и аналитическим методами:
1. Графический метод. Заключается в построении точного графика выровненного динамического ряда, на котором линию полученного тренда продлевают до интересующей нас даты.
2. Аналитический метод. При данном методе в рассчитанное аналитическое уравнение подставляют номер интересующего нас периода.
При построении динамического ряда по стоимостным показателям, выраженным в рублях, в целях исключения влияния инфляции фактические цены необходимо выразить или в сопоставимых ценах за какой-то год, или в условных единицах, например, в $ или €, другой «твердой» валюте.
|
|
|
Дата добавления: 2018-02-15; просмотров: 717; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
