Статистический анализ динамических рядов. Показатели динамического ряда
Показатели динамического ряда
Абсолютный прирост  рассчитывается как разность двух уровней динамического ряда, один из которых принят за базу сравнения.
рассчитывается как разность двух уровней динамического ряда, один из которых принят за базу сравнения.
Цепной абсолютный прирост рассчитывается по формуле:
 , (7.1)
, (7.1)
Базисный абсолютный прирост:
 , (7.2)
, (7.2)
Коэффициент роста  – отношение текущего уровня ряда динамики к уровню, принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в %
– отношение текущего уровня ряда динамики к уровню, принятому за базу сравнения. Коэффициент роста, умноженный на 100, называется темпом роста в % 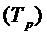 .
.
1. Если динамический ряд обозначить как  , то:
, то:
· цепной коэффициент (темп) роста рассчитывается как:
 ,
, 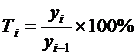 , (7.3)
, (7.3)
· базисный коэффициент (темп) роста рассчитывается как:
 ,
,  , (7.4)
, (7.4)
Коэффициент (темп) роста всегда – число положительное.
Коэффициент (темп) прироста  показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%). Рассчитывается двумя способами:
показывает, на сколько частей (процентов) увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 1 (100%). Рассчитывается двумя способами:
Первый способ - как отношение абсолютного прироста к базисному уровню.
1. Если динамический ряд обозначить как 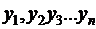 , то:
, то:
· цепной коэффициент (темп) прироста рассчитывается как:
 ,
, 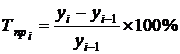 , (7.5)
, (7.5)
· базисный коэффициент (темп) прироста рассчитывается как:
 ,
, 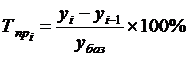 (7.6)
(7.6)
Второй способ – коэффициент (темп) роста минус 1 (100).
|
|
|
 или
или  , (7.7)
, (7.7)
Коэффициент (темп) прироста может быть как положительным, так и отрицательным.
Абсолютное значение одного процента прироста показывает часть абсолютного прироста, которая обеспечила 1% относительного прироста. Рассчитывается двумя способами.
Первый способ – как отношение абсолютного прироста к темпу прироста за тот же период:
 , (7.8)
, (7.8)
Второй способ – как 0,01 часть от предыдущего (базисного) уровня:
 , (7.9)
, (7.9)
Средний абсолютный прирост (средняя скорость роста)  определяется как средняя арифметическая из показателей абсолютного прироста:
определяется как средняя арифметическая из показателей абсолютного прироста:
 , (7.10)
, (7.10)
где 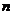 - количество абсолютных приростов.
- количество абсолютных приростов.
Средний коэффициент (темп) роста рассчитывается по формуле средней геометрической из индивидуальных коэффициентов (темпов) роста, так как необходимо учитывать то обстоятельство, что скорость развития явления идет по правилам сложных процентов, где накапливается процент на процент.
 , (7.11)
, (7.11)
где  - знак произведения;
- знак произведения;
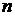 – число коэффициентов роста.
– число коэффициентов роста.
Средний коэффициент (темп) прироста рассчитывают как:
|
|
|
 или
или  , (7.12)
, (7.12)
Тренд – основная тенденция (к снижению или увеличению) развития изучаемого явления.
Методы выявления тренда в динамических рядах.
Метод средних. Данный метод заключается в том, что изучаемый динамический ряд разбивается на несколько интервалов, как правило, на два. По каждому интервалу рассчитывается групповая средняя  . Далее выдвигается гипотеза о существенных различиях между средними. Если данная гипотеза принимается, то наличие тренда признается.
. Далее выдвигается гипотеза о существенных различиях между средними. Если данная гипотеза принимается, то наличие тренда признается.
Фазочастотный критерий знаков первой разрядности. Данный метод основан на анализе ряда абсолютных цепных приростов (разностей первого порядка) исходных уровней динамического ряда. Фазой называется изменение знаков 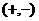 абсолютных приростов. Если в ряду абсолютных приростов отсутствуют фазы (любо их количество невелико), то в данном динамическом ряде наблюдается тренд.
абсолютных приростов. Если в ряду абсолютных приростов отсутствуют фазы (любо их количество невелико), то в данном динамическом ряде наблюдается тренд.
Критерий Кокса и Стюарта. Исследуемый динамический ряд разбивается на три группы с равным количеством уровней (при недостаточном количестве уровней их необходимо добавить). Далее сравниваются уровни крайних групп
Метод серий. При данном методе все уровни изучаемого динамического ряда разбиваются по двум типам. Например если уровень меньше среднего значения, или медианного уровня то он имеет тип А, если больше то В. Серией называется любая последовательность уровней одинакового типа, граничившего с уровнями другого типа. Рассмотрим две последовательности.
|
|
|
1. BBBBBBBAAAAAAA
2. AABBAAABBAB
В первом примере число серий  .
.
Во втором случае 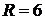 .
.
Если в исследуемом динамическом ряду тенденция развития отсутствует, то количество серий будет величиной случайной, распределенной приближенно по нормальному закону (для  ). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале
). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале  .
.
Величина  (величина нормированного отклонения) задается в таблицах нормального распределения вероятностей в соответствии с принятым уровнем
(величина нормированного отклонения) задается в таблицах нормального распределения вероятностей в соответствии с принятым уровнем  (табл. 19).
(табл. 19).
Таблица 19

| 
|
| 1,0 | 0,683 |
| 1,5 | 0,866 |
| 2,0 | 0,954 |
Среднее число серий рассчитывается как:
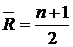 , (7.13)
, (7.13)
Среднее квадратическое отклонение числа серий:
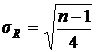 , (7.14)
, (7.14)
где 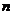 – число уровней ряда.
– число уровней ряда.
Выражение для доверительного интервала приобретает вид:
|
|
|
 , (7.15)
, (7.15)
Границы полученного доверительного интервала округляют до целых чисел, уменьшая нижнюю границу и увеличивая верхнюю.
Если число серий 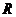 в исследуемом динамическом ряду попадает в доверительный интервал, то тенденция развития в нем отсутствует.
в исследуемом динамическом ряду попадает в доверительный интервал, то тенденция развития в нем отсутствует.
Дата добавления: 2018-02-15; просмотров: 623; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
