Косой изгиб. Определение напряжений и положения нейтральной линии. Определение перемещений.
Вид нагружения, когда плоскость действия нагрузки не совпадает не из одной из главных плоскостей но совпадает с центром тяжести
. Косой изгиб момента не совпадает ни с одной из глав. Под косым изгибом понимается такой случай изгиба, при котором плоскость изгибающего ных плоскостей инерции стержня.
Задачу косого изгиба сводят к одновременному рассмотрению двух плоских (прямых ) изгибов, раскрывая изгибающий момент в сечении на 2 момента, действуя в главных плоскостях (проходят через главные оси сечения) Т.к. напряжение от силы Q является второго напряжения порядка от изгиба.
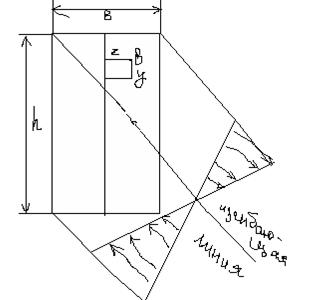Схема сил при косом изгибе.
На рис. показан консольный стержень , нагруженный силой F, действующий перпендикулярно его оси и составляющей угол φ с главной плоскостью ху. Напряжение в некоторой точке В поперечного сечения на расстоянии х от незакрепленного торца. Моменты, изгибающие стержень в вертикальной и горизонтальной плоскостях х.
Где Fу и Fz - вертикаль и горизонталь, составляющие силы.
F,M- составляющие моменты в сечении
Напряжения и нейтральная ось при косом изгибе.Нормальное напряжение в нейтральной точке с координатами у и z определяются суммой напряжений от моментов Му и Мz т.е. 
Максимальное напряжение будет действовать в точках наиболее удаленных от нейтральной линии.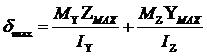 
Положение нейтральной линии при косом изгибе найдем из уравнения полога δ=0 обозначая координаты нейтральной линии Y0 и Z0 получим 
|
|
|
Видно что нейтральная линия является прямой проходящей через начало координат (центр тяжести поперечного сечения) обозначая через α угол наклона нейтральной линии к оси Z найдем 
Определение перемещений при косом изгибе
Перемещения при косом изгибе определяют по принципу независимости действия сил, т.е. рассчитывают прогибы 
в направлении главных осей, а величину полного прогиба в любом сечении балки получают геометрическим суммированием: 
.
Например, для балки, изображенной на рис.7.13, прогиб конца консоли определится следующим образом:
Направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы (рис.7.13).
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:
1) проверка прочности;
2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy];
3) проверка по несущей способности (определить M).
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:
|
|
|
- построить эпюры внутренних усилий (изгибающих моментов). Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно горизонтальной оси , горизонтальная – относительно оси ;
- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;
- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
- записать условие прочности в этих точках. Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.
Дата добавления: 2018-02-15; просмотров: 3039; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!