Влияние повторных нагрузок за пределом текучести на механические свойства материалов (наклеп)
Явление повышения предела пропорциональности после пластической деформации материала при повторном нагружении называется наклепом
Наклеп во многих случаях является нежелательным явлением, так
как наклепанный металл становится более хрупким. Наклеп можно уст-
ранить при помощи специальной термической обработки
Однако в целом ряде других случаев наклеп полезен и его создают
искусственно, например, в деталях, подвергающихся воздействию пе-
ременных нагрузок.
Площадь сечения. Статические моменты. Определение центра тяжести сечения, центральные оси. Осевые, полярные и центробежные моменты инерции. Изменение моментов инерции при параллельном переносе осей. Главные моменты инерции. Радиусы инерции. Эллипс инерции.
Геометрические характеристики плоских сечений.
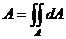- площадь сечения.
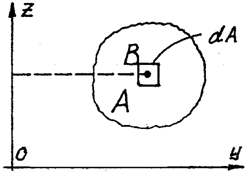
| Статическими моментами ппощади сечения относительно осей X и У (рис.4.3) называются определенные интегралы вида: |
|
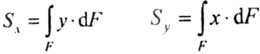
| где F - площадь сечения; X и у - координаты элемента площади dF. |
| Если известно положение центра тяжести сечения (рис. 4.4). то статические моменты сечения могут быть подсчитаны по простым формулам, без взятия интегралов, а именно не F а A в формуле |
|
| где Xc и Yc - координаты центра тяжести сечения. |
| Из выражений (2) можно определить координаты центра тяжести сечения Xc и Yc: |
|
Определение центра тяжести сечения:
|
|
|
По известной из теоретической механике теореме о моменте равнодействующей можно написать
(1.2)
где А - площадь всей фигуры (равнодействующая); ус - расстояние от центра тяжести фигуры до оси х.
Из формулы (1.2) следует формула определения ординаты центра тяжести
ус = Sx/A. (1.3)
Аналогично, статический момент относительно оси у равен
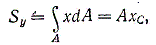(1.4)
Откуда
xс = Sy/A. (1.5)
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.
| Статический момент сечения относительно оси, проходящей через центр тяжести, равен нулю. |
Оси, проходящие через центр тяжести сечения -называются центральными. Центр тяжести сечения лежит на оси симметрии сечения. Если сечение имеет хотя бы две оси симметрии, то центр тяжести лежит на пересечении этих осей.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
|
|
|
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
Осевые моменты инерции некоторых тел.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
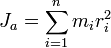где:
· mi — масса i-й точки,
· ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, какмасса тела является мерой его инертности в поступательном движении.
,
где:
· 
— масса малого элемента объёма тела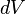 
,
· 
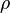— плотность,
· 
— расстояние от элемента 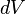до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
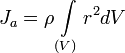
Jy=интегр(z^2dA)
Jz=integ(y^2dA) круг: Jz=Jy=(ПR^4)/4 прямоуг:Jy=bh^3/12 Jz=b^3h/12
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
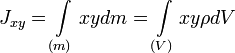
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
|
|
|
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — егоглавными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции
Jyz=integ(yzdA)
Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:
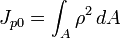
Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, cм4) и может быть лишь положительной.
Дата добавления: 2018-02-15; просмотров: 641; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!