Кручение стержней кругового (сплошного и полого) сечения. Чистый сдвиг как частный случай плоского напряженного состояния. Условия прочности и жестокости.
Кручение стержней- такой вид деформации ,при котором сечения плоско и параллельно поворачиваются относительно друг друга .Поворот происходит относительно оси стержня.
Допущения при выводе формул
1-Все сечения до и после деформации остаются плоскими.
2-Отсутствуют нормальные напряжения
Закон Гука при кручении:O`=Mкр/G*Jро Jро=ПR^4/2 Wро=ПR^3/2
Чистый сдвиг – частный случай плоского напряженного состояния когда отсутствуют нормальные напряжения.
Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.
Условие прочности при растяжении (сжатии) выражается неравенством:
Tmax=Mкр.max/Wро<[T]
:n – коэффициент запаса прочности, устанавливаемый нормативными документами.
Условие жесткости
Условие жесткости стержня
O`(погонный угол закр.)=Mкрmax/G*Jро<[O]
Критерии пластичности и разрушения. Первая, вторая, третья и четвертая теории прочности. Тория Мора. Общие сведения о различных гипотезах прочности и пластичности. Общий план решения задачи о проверки прочности.
В общем случае опасное напряженное состояние элемента конструкции зависит от соотношения между тремя главными напряжениями (s1,s2,s3). Т.е., строго говоря, для каждого соотношения нужно экспериментально определять величину предельного напряжения, что нереально. Поэтому были приняты такие методы расчета прочности, которые позволяли бы оценить степень опасности любого напряженного состояния по напряжению растяжения — сжатия. Они называются теориями прочности (теории предельных напряженных состояний).
1-ая теория прочности (теория максимальных нормальных напряжений)Установил Кулон: При любом напр. состоянии хрупкое разрушение будет, если макс. норм. напряжение достигает предельного значения для данногоматериала Главный недостаток: не учитываются два других главных напряжения. Подтверждается опытом только при растяжении весьма хрупких материалов (стекло, гипс). В настоящее время практически не применяется.
Условия разрушения:
сигма max<сигма пред.(экспиремент на растяжение)
сигма экв.=сигма гл. <[сигма]доп.
2-ая теория прочности (теория максимальных относительных деформаций):При любом напр. сос-ии хрупкое разр. будет если макс. относит. дефор-ии достигнут пред. знач.
Условие разр-ия: епсилон max= епсилон пр.
ус-ие прочности: σэкв.=σ1-V(ню)*(σ2+σ3)<[σ]доп.
3-я теория прочности (теория максимальных касательных напряжений): При При любом напр. сос-ии пластич. разр. будет если макс касательные напряжения достигнут пред. состояния tmax = tпред., tmax=σ1-σ3/2, условие прочности: σэквIII= σ1— σ3≤ [σ]. Основной недостаток — не учитывает влияние s2.
При плоском напряженном состоянии: sэквIII= £ [s]. При sy=0 получаем Широко используется для пластичных материалов.
4-я теория прочности (энергетическая теория) При любом напр. состоянии разр. будет если удельная работа по изменению формы достигнет пред. значения.
σэкв=корень из{0.5*[(σ1-σ2)^2+(σ2-σ3)^2+(σ3-σ1)^2]}≤[σ]
Учитывает, все три главных напряжения.
Широко используется для пластичных материалов.
Теория прочности Мора Получена на основе кругов напряжений Мора. . Используется при расчетах хрупких материалов, у которых допускаемые напряжения на растяжение [sp] и сжатие [sс] не одинаковы (чугун).
Для пластичных материалов [sp]=[sс] теория Мора превращается в 3-ю теорию.
σэкв.=σ1-σв(+)/σв(-)*σ3≤[σ]
Круг Мора(круг напряжений). Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси s из центра С луч под углом 2a (a>0, то против час.стр.), находим точку D,
координаты которой: sa,ta. Можно графически решать как прямую, так и обратную задачи.
Общий план решения задачи о проверки прочности:
1) Проверяем условие прочности ( Для хрупких материалов исп 1, 2 теорию прочности и Теорию прочности Мора; Для пластичных материалов 3ая и 4ая теория прочности)
2) Определяем действительный коэффициент запаса прочности.(n(действ.))
3) Находим опасное сечение.
для 1ой и 2 ой теор. Прочности: опасное сечение – это площадка перпендикулярная первому главному направлению
для 3ей и 4ой теор. Опасное сечение – плозадка на которой действ. Истинный максимум касательных напряжений. И для 4 оп.сеч – октаэдрическая площадка, т.е. равно наклоненная по всем 3ем осям.
Чистый и поперечный изгиб , типы опорных связей , определение спорных реакций. Внутренние усилия при плоском изгибе и связь между ними. Эпюры перерезывающих сил и изгибающих моментов. Дифференциальные зависимости между q, M и Q .
Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб.
Стержни, которые работают преимущественно на изгиб, называют балками (применяются в конструкциях зданий разнообразного назначения, мостах, в виде под крановых балок производственных зданий и т. д.). Они обладают простотой конструкции, изготовления и надежностью в работе.
Виды опор.
Шарнирно'подвижная опора.Эта опора является устройством, допускающим перемещение опорного сечения параллельно опорной плоскости и поворот его в вертикальной плоскости относительно оси цилиндрического шарнира. Это устройство не дает возможности перемещаться в направлении наложенной связи по вертикали. Реакция шарнирно_подвижной опоры VA направлена вдоль опорной связи.
Шарнирно'неподвижная опора.Эта опора не допускает смещений опорного сечения ни в продольном, ни в поперечном направлениях, однако допускает поворот этого сечения относительно шарнира. Шарнирно неподвижная опора представляет собой опору с двумя связями, которые удобно прикладывать по направлению оси балки и перпендикулярно оси балки. В этой опоре появляются две составляющие опорной реакции: HA и VA.
Жесткое закрепление или заделка.Эта опора не допускает поворота опорного сечения и перемещения его ни в каком направ_лении — на это сечение наложены три связи: вертикальная VA, горизонтальная НА, составляющие опорной реакции, и изгибающий момент МА.
Если в балке сечением, имеющим вертикальную ось, внешняя нагрузка и реактивные усилия лежат в одной плоскости, совпадающей с осью сечения, то балка будетизгибаться в той же плоскости. Такой изгиб называют плоским.
Пусть при плоском изгибе внешняя нагрузка перпендикулярна продольной оси балки, тогда в поперечных сечениях балки возникают лишь поперечная сила и изгибающий момент, а продольная сила равна нулю. Такой изгиб называют поперечным.
Дифференциальные зависимости между q, M и Q .
1) 
2) 
3) 
Нормальные напряжения при чистом изгибе – гипотеза плоских сечений, нейтральная ось, определение напряжений. Максимальные нормальные напряжения при изгибе, момент сопротивления сечения, равнопрочные балки.
Гипотеза плоских сечений: сечения, перпендикулярные оси стержня и плоские до деформации остаются такими же и после приложения нагрузки.
От действия изгибающего момента в поперечных сечениях балки возникают нормальные напряжения, определяемые по формуле
 ,где М – изгибающий момент в рассматриваемом сечении;
,где М – изгибающий момент в рассматриваемом сечении;
I – момент инерции поперечного сечения балки относительно нейтральной оси;
у – расстояние от нейтральной оси до точки, в которой определяются напряжения.
Из формулы (8.1), нормальные напряжения в сечении балки по ее высоте линейны, достигая максимального значения в наиболее удаленных точках от нейтрального слоя.
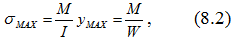 ,где W – момент сопротивления поперечного сечения балки относительно нейтральной оси. В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности. Следовательно, сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений.
,где W – момент сопротивления поперечного сечения балки относительно нейтральной оси. В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности. Следовательно, сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечений.
Нейтральная ось — линия в поперечном сечении изгибаемой балки, в точках которой нормальные напряжения, параллельные оси балки, равны нулю. Нейтральная ось делит сечение на две части, в одной из которых действуют растягивающие нормальные напряжения, а в другой — сжимающие.
Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию от оси до наиболее удаленной точки поперечного сечения

Дата добавления: 2018-02-15; просмотров: 810; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
