Эффектом Доплера называют изменение частоты колебаний, воспринимаемых приемником при движении приемника и источника относительно друг друга. 13 страница
Задача 2. Определить коэффициент трения между телом и наклонной плоскость, на которой оно покоится, если угол наклона плоскости α = 30о.
Решение
На чертеже изображают все силы, действующие на тело (рис. 7.7) и записывают уравнение равновесия в векторном виде:

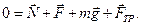
Выбираем оси координат OX и OY. Записываем уравнение равновесия в проекциях на выбранные оси:
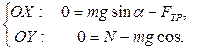
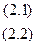
Из уравнения (2.2) определяем силу реакции опоры:
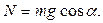
По определению силы трения скольжения:
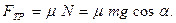
Полученное значение силы трения подставляем в уравнение (2.1) и коэффициент трения:
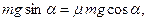
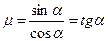 .
.
 Задача 3. Определить положение центра тяжести однородной круглой пластины радиусом R = 0,5 м, в которой вырезано квадратное отверстие со стороной
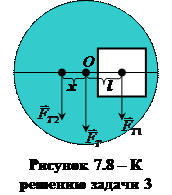
Задача 3. Определить положение центра тяжести однородной круглой пластины радиусом R = 0,5 м, в которой вырезано квадратное отверстие со стороной  так, как указано на рисунке 7.8.
так, как указано на рисунке 7.8.
Решение
Относительно центра тяжести фигуры результирующий момент сил, действующих на тело, равен нулю: 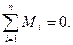 Если вставить вырезанную часть пластинки на прежнее место, то силу тяжести всей пластинки FT можно представить как сумму двух параллельных сил – силы тяжести вырезанной части FT1 и силы тяжести оставшейся фигуры FT2:
Если вставить вырезанную часть пластинки на прежнее место, то силу тяжести всей пластинки FT можно представить как сумму двух параллельных сил – силы тяжести вырезанной части FT1 и силы тяжести оставшейся фигуры FT2:
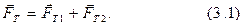
Уравнение моментов относительно точки О будет иметь вид:
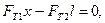 или
или 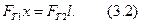
Из уравнения (3.1) получаем 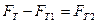 и подставляем в уравнение (3.2):
и подставляем в уравнение (3.2):

По определению силы тяжести:
 ,
,
где ρ – плотность материала, из которого изготовлена пластинка, S – площадь пластинки, h – ее высота, S1 – площадь вырезанной части.
Тогда получаем выражение для положения центра тяжести однородной круглой пластины x:
|
|
|
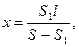
где 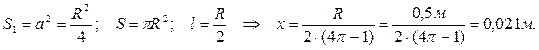
Задача 4. Как надо положить книги, чтобы составить наклонную стопку?
Решение
 Стопка книг не рассыплется, если расставлять их так, чтобы центр тяжести всех книг, находящихся выше некоторой произвольно выбранной книги, лежал на вертикали, проходящей через эту книгу. Это условие должно выполняться для любой книги в стопке.
Стопка книг не рассыплется, если расставлять их так, чтобы центр тяжести всех книг, находящихся выше некоторой произвольно выбранной книги, лежал на вертикали, проходящей через эту книгу. Это условие должно выполняться для любой книги в стопке.
Задача 5. Постройте, как в цирке, фигуру из домино (рис. 7.9).
Решение
Если стол совершенно горизонтален и прочно стоит на полу, можно выстроить фигуру из домино. Сначала надо поставить стоймя три косточки домино, – на них возвести такую хрупкую постройку легче, чем на одной кости. Потом, когда все будет построено, осторожно убирают две крайние косточки, которые служили подпорками, и ставят их на вершину всего непрочного здания.
Равновесие здесь вполне возможно; нужно только, чтобы перпендикуляр, опущенный из центра тяжести всей конструкции, прошел через основание нижней косточки домино.
Вопросы и задания для самоконтроля
1. Что изучает статика? В чем заключается различие между динамикой и статикой? Рассмотрите историю создания статики как науки и составьте свою хронологическую таблицу ее развития.
|
|
|
2. Какая точка твердого тела называется центром тяжести? Как определяется центр тяжести твердого тела? Как связаны между собой центр тяжести и центр масс твердого тела?
3. Какое состояние твердого тела называется равновесием? Сформулируйте два условия равновесия. Какие виды равновесий различают? Дайте им определения и приведите примеры их проявления в природе, быту и т.д.
4. В чем заключается теория рычага великого Архимеда?
5. Какое механическое устройство называется кардановым подвесом? Нарисуйте его схему.
8. Поставьте неваляшку (Ваньку-встаньку) на шероховатую доску и слегка приподнимите один из концов доски, как это показано на рис. 7.10. Как Вы думаете, в какую сторону отклонится голова игрушки при сохранении её равновесия? Правильно ли это явление изображено на рисунке?
9.  Для сохранения в неизменном положении предметов при движении их опоры уже много столетий применяется так называемый карданов подвес – устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. В качестве примера можно рассмотреть корабельную керосиновую лампу. При любой качке на море благодаря вращающемуся карданову подвесу лампа всегда сохраняет вертикальное положение. Нарисуйте схему корабельной керосиновой лампы, прикрепленной к вращающемуся карданову подвесу.
Для сохранения в неизменном положении предметов при движении их опоры уже много столетий применяется так называемый карданов подвес – устройство, в котором центр тяжести тела располагают ниже осей, вокруг которых оно может вращаться. В качестве примера можно рассмотреть корабельную керосиновую лампу. При любой качке на море благодаря вращающемуся карданову подвесу лампа всегда сохраняет вертикальное положение. Нарисуйте схему корабельной керосиновой лампы, прикрепленной к вращающемуся карданову подвесу.
|
|
|
10. На рис. 7.11 изображены два положения грузовой машины. Объясните, почему на фото а машина стоит устойчиво, а на фото б – эта же машина опрокинулась.
11. 
 |
В одном случае два человека тянут за концы каната в противоположные стороны с равными силами F. В другом случае один конец каната привязан к неподвижной опоре, а за другой его конец тянут два человека с теми же силами F. Какое натяжение испытывает канат в обоих случаях?
12. Что человеку делать легче: 1) тянуть груз? 2) толкать груз? Почему? Ответ обоснуйте. По каждому из этих рисунков 7.13 составьте и решите задачи.
13. Объясните причину смешения грузов от положения равновесия в грузовом отсеке автомобиля, изображенных на рис. 7.12.
 |
14.  При взвешивании на неравноплечих весах рычажных весах масса тела (по сумме весов положенных гирь) на одной чаше весов оказалась равной 2,2 кг, а на другой – 3,8 кг. Определить истинную массу груза.
При взвешивании на неравноплечих весах рычажных весах масса тела (по сумме весов положенных гирь) на одной чаше весов оказалась равной 2,2 кг, а на другой – 3,8 кг. Определить истинную массу груза.
15.  Тяжелый цилиндрический каток необходимо поднять на ступеньку высоты h. Определить наименьшую силу F, которую необходимо для этого приложить к центру катка в горизонтальном направлении, если каток имеет радиус R, а масса катка равна М (рис. 7.14).
Тяжелый цилиндрический каток необходимо поднять на ступеньку высоты h. Определить наименьшую силу F, которую необходимо для этого приложить к центру катка в горизонтальном направлении, если каток имеет радиус R, а масса катка равна М (рис. 7.14).
|
|
|
16. К концам груза массой 10 кг и длиной 40 см подвешены грузы массами 40 кг и 10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?
17. Масса Луны составляет 1,2 % массы Земли. Расстояние между их центрами 384000км. Где расположен центр масс системы «Земля — Луна»?
18. Объясните причину устойчивого равновесия огромной глыбы, изображенной на фото (рис. 7.16)
19. Определить положение центра тяжести однородной квадратной пластины со стороной а = 0,18 м, в которой вырезано квадратное отверстие со стороной а = 0,2 м как показано на рисунке 7.15 к задаче.
Рекомендованная литература
1. Евграфова Н.Н., Каган В.Л. Курс физики. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1978. – 512 с. – С. 48-57.
2. Кудрявцев П.С. Курс истории физики: Учебное пособие для студентов пед. ин-тов по физ. спец. – 2-е изд., испр. и доп. – М. : Просвещение, 1982. – 448 с. – С. 30-34.
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
План
1. Механические колебания. Уравнения малых колебаний.
2. Свободные гармонические колебания.
3. Пружинный осциллятор.
4. Физический маятник.
5. Математический маятник.
6. Затухающие колебания.
7. Вынужденные колебания.
8. Резонанс.
9. Автоколебания.
10. Примеры использования механических колебаний.
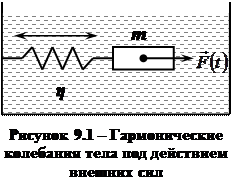
Мы живем в мире колебаний. Маятник стенных часов, фундамент быстроходной турбины, кузов железнодорожного вагона, струна гитары и т.д. совершают различные колебания.
По современным воззрениям, все звуковые, тепловые, световые, электрические и магнитные явления, то есть важнейшие физические процессы окружающего нас мира, сводятся к различным формам колебания материи. Колебания играют важную роль в таких ведущих областях техники, как электричество, радио, телекоммуникации. Выработка, передача и потребление электрической энергии, телефония, радиовещание, телевидение, радиолокация – все эти важные отрасли основаны на использовании электрических и электромагнитных колебаний. С колебаниями мы встречаемся и в живом организме. Биение сердца, сокращение желудка, деятельность кишечника имеют колебательный характер. Строители и механики имеют дело с колебаниями сооружений и машин. Кораблестроители – с качкой и вибрацией корабля и т.д.
Из истории науки. Уже в студенческие годы великий итальянский ученый Галилео Галилей (1564-1642) увлекался изучением колебаний. Он обнаружил, что колебания маятника не зависят от его массы, а определяются длиной подвеса. Сохранилось предание о том, как молодой студент медицинского факультета Г. Галилей в одно из воскресений 1583 года с интересом следил за качаниями зажженных лампад в церкви. По ударам пульса он определил время, необходимое для полного размаха лампад. С этого времени медицину пришлось ему оставить и сосредоточиться на физике.
Г. Галилей опубликовал исследование колебаний маятника и заявил, что период колебаний не зависит от их амплитуды (это приблизительно верно для малых амплитуд). Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Г. Галилея привлекли внимание Х. Гюйгенса (1629-1695).
В 1673 году выходит в свет сочинение Х. Гюйгенса «Маятниковые часы». В этом сочинении ученый устанавливает, что свойством изохронности обладает циклоида, и разбирает математические свойства циклоиды.
В 1657 году Х. Гюйгенс издал описание устройства изобретённых им часов с маятником. В то время учёные не располагали таким необходимым для экспериментов прибором, как точные часы. Г. Галилей, например, при изучении законов падения считал удары собственного пульса. Часы с колесами, приводимыми в движение гирями, были в употреблении с давнего времени, но точность их была неудовлетворительна. Маятник же со времен Г. Галилея употребляли отдельно для точного измерения небольших промежутков времени, причём приходилось вести счёт числу качаний. Часы Х. Гюйгенса обладали хорошей точностью, и учёный далее неоднократно, на протяжении почти 40 лет, обращался к своему изобретению, совершенствуя его и изучая свойства маятника. Х. Гюйгенс намеревался применить маятниковые часы для решения задачи определения долготы на море, но существенного продвижения не добился. Надёжный и точный морской хронометр появился только в 1735 году в Великобритании.
В 1673 году в первой части труда «Маятниковые часы» Х. Гюйгенс описывает усовершенствованный, циклоидальный маятник, который обладает постоянным временем качания независимо от амплитуды. Для объяснения этого свойства автор посвящает вторую часть книги выводу общих законов движения тел в поле тяжести – свободных, движущихся по наклонной плоскости, скатывающихся по циклоиде. Это усовершенствование не нашло практического применения, поскольку при малых колебаниях повышение точности от циклоидального привеса незначительно. Однако сама методика исследования вошла в золотой фонд науки.
В четвёртой части Х. Гюйгенс изложил теорию физического маятника. Х. Гюйгенс решает ту задачу, которая не давалась стольким современным ему геометрам, – задачу об определении центра качаний. Он основывается на следующем предложении: «Если сложный маятник, выйдя из покоя, совершил некоторую часть своего качания, большую полуразмаха, и если связь между всеми его частицами будет уничтожена, то каждая из этих частиц поднимется на такую высоту, что общий центр тяжести их при этом будет на той высоте, на которой он был при выходе маятника из покоя».
Это предложение, не доказанное у Х. Гюйгенса, является у него в качестве основного начала, между тем как теперь оно представляет простое следствие закона сохранения энергии.
Теория физического маятника дана Х. Гюйгенсом в общем виде и в применении к телам разного рода. Х. Гюйгенс исправил ошибку Г. Галилея и показал, что провозглашённая последним изохронность колебаний маятника имеет место лишь приближённо.
1 Механические колебания. Уравнение малых колебаний
В общем случае колебаниями называют любые периодические движения, ограниченные в пространстве. Из всех возможных выделяют гармонические колебания, реализующиеся при малых амплитудах.
Пусть на тело, помещенное в вязкую среду (рис. 9.1), действуют постоянная во времени сила 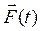 и упругая сила
и упругая сила 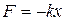 . В этом случае при малых колебаниях возникает сила вязкого трения:
. В этом случае при малых колебаниях возникает сила вязкого трения:
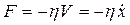 .
.
Запишем II закон Ньютона для тела, массой m, помещенного в вязкую среду:
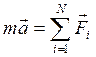 ,
,
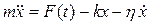 ,
,
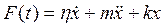 .
.
Последнее уравнение представляет собой дифференциальное уравнение малых колебаний. Каждое слагаемое этого уравнения делим на m:
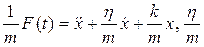 ,
,
где 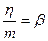 – коэффициент затухания,
– коэффициент затухания,
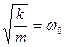 – частота собственных колебаний.
– частота собственных колебаний.
С учетом коэффициента затухания и частоты собственных колебаний дифференциальное уравнение малых колебаний запишется в виде:
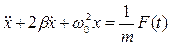 .
.
2 Свободные гармонические колебания
В случае отсутствия сопротивления среды, т.е. затухания ( 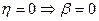 ), уравнение малых колебаний
), уравнение малых колебаний 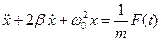 принимает вид уравнения гармонических колебаний или уравнения гармонического осциллятора:
принимает вид уравнения гармонических колебаний или уравнения гармонического осциллятора:
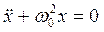 .
.
Осциллятор (от лат. – качаюсь) – система, совершающая колебания, то есть показатели которой периодически повторяются во времени. Понятие осциллятора играет важную роль в теории твёрдого тела, электромагнитных излучений, колебательных спектров молекул. Примеры простейших осцилляторов – маятник и колебательный контур.
Решение уравнения малых колебаний ищется в виде:
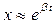 ,
, 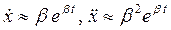 ,
,
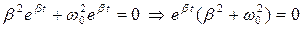 .
.
Так как 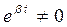 , то
, то 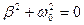 . Следовательно,
. Следовательно, 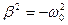 , а
, а 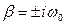 .
.
Используя формулу Эйлера: 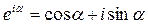 , выделяем вещественную часть и получаем решение гармонических колебаний в виде:
, выделяем вещественную часть и получаем решение гармонических колебаний в виде:
 ,
,
где a 0 – амплитуда – наибольшее отклонение от положения равновесия; ( 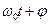 ) – фаза колебаний – характеризует состояние системы в любой момент времени; φ0 – начальная фаза – показывает состояние системы в начальный момент времени; ω0 – циклическая частота колебаний – количество колебаний за 2π секунд,
) – фаза колебаний – характеризует состояние системы в любой момент времени; φ0 – начальная фаза – показывает состояние системы в начальный момент времени; ω0 – циклическая частота колебаний – количество колебаний за 2π секунд, 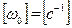 :
:
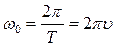 ,
,
υ – частота колебаний – количество колебаний в единицу времени (за одну секунду),  ;
;
Т – период колебаний – время одного колебания, 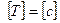 :
:
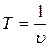 .
.
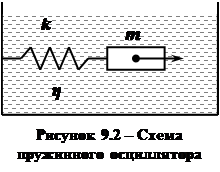
3 Пружинный осциллятор
Собственная частота колебаний пружинного осциллятора (рис. 9.2) равна:
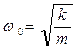 .
.
Тогда уравнение гармонических колебаний пружинного осциллятора принимает вид:
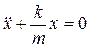 ,
,
а его период колебаний определяется по формуле:
Дата добавления: 2021-05-18; просмотров: 75; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
