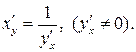Тема: Производная и ее геометрический смысл. Правила дифференцирования
Цель: сформировать умение находить производные функций, заданных в явном виде, знать геометрический смысл производной.
Теоретические сведения к практическому занятию:
Производной функции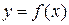 
называется конечный предел отношения приращения функции 
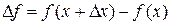к приращению независимой переменной 
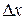при стремлении последнего к нулю:
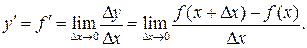(1)
Обозначения производной в точке х0:
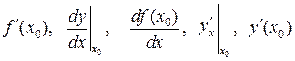и другие.
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.
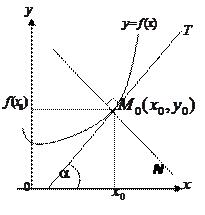Геометрический смысл производной .
Если кривая задана уравнением ,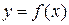
то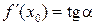 
— угловой коэффициент касательной к графику функции в этой точке ( 
).
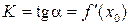Уравнение касательной к кривой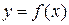
в точке х0 (прямая М0Т) имеет вид:
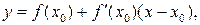(2)
а уравнение нормали (М0N):
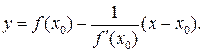(3)
Правила дифференцирования
| № пп | U = u(x), V=V(x) — дифференцируемые функции | № пп | U = u(x), V=V(x) — дифференцируемые функции |
| I |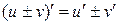 
| VI | Производная сложной функции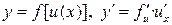 
|
| II |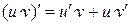 
| VII | Функция задана параметричес-кими уравнениями |
| III |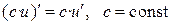 
| ||
| IV |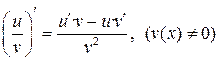 
| VIII | Если |
| V |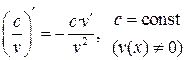 
|
—
Пример 1. Найти производные функций:
а)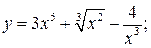 
б) 
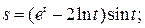в)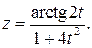 
|
|
|
Решение.
а) Используя правила I, III и формулу (3), получим:
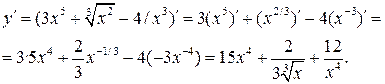
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t=1, получим:
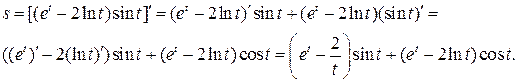
в) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t=1, получим:
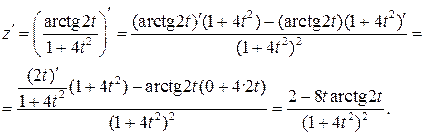
Пример 2. Составить уравнение касательной и нормали к кривой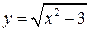 
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 
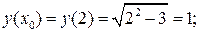
2) 
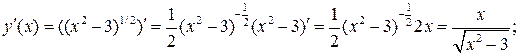
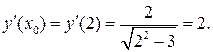
Подставим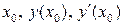 
в уравнения и получим: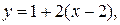 
или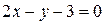 
— уравнение касательной.
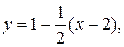или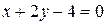 
— уравнение нормали.
Пример 3. Найти дифференциалы функций:
а)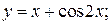 
б) 
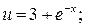в)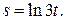 
Для дифференциала функции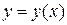 
справедлива формула 
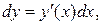т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а)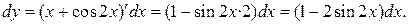 
б)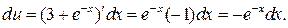 
в)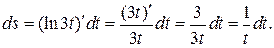 
Самостоятельная работа:
Задание 1. Найти производные 1-го порядка данных функций
1) 
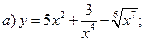
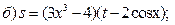
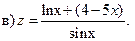
2) 
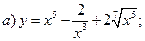
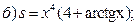
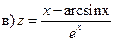
3) 
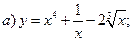
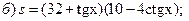
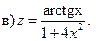
Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1) 
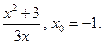12
2) 
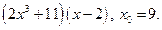
3) 
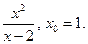
Задание 3. Выполните доклад на тему «История возникновения и развития производной функции»
Содержание практического занятия:
А. Ответить на вопросы:
|
|
|
1) Дать определение производной функции. Привести примеры.
2) В чем заключается геометрический смысл производной?
3) Укажите основные правила дифференцирования функций. Приведите примеры.
4) Дать определение дифференцирования функции.
5) Укажите основные формулы для дифференцирования производных элементарных функций. Приведите примеры.
Б. Выполнить задания:
Задание 1. Найти производные 1-го порядка данных функций
1) 
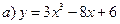
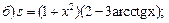
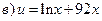
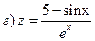
2) 
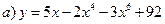
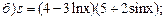
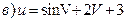
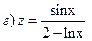
3) 
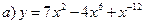
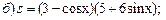
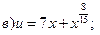
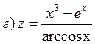
Задание 2. Составить уравнение касательной и нормали к кривой y=f(x) в точке с абсциссой х0.
1) 
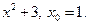
2) 
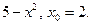
3) 
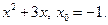
4) 
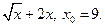
Задание 3. Найти дифференциалы функций:
1) 
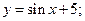
2) 
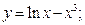
3) 
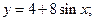
4) 
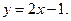
5) 
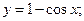
6) 
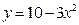
Дата добавления: 2021-04-15; просмотров: 115; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!
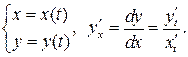
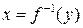