Тема: Применение определенного интеграла для вычисления площадей фигур
Цель: сформировать умение применять определенный интеграл для вычисления площадей фигур
Теоретические сведения к практическому занятию:
Площади плоских фигур
1. Вычисление площадей плоских фигур в декартовой системе координат
Если плоская фигура (рис. 1) ограничена линиями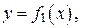 
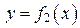, где 
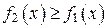для всех 
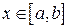, и прямыми 
, 
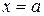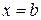, то ее площадь вычисляется по формуле:
(*)
| 
|
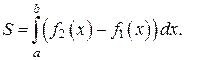| Рис. 1 | Рис. 2 |
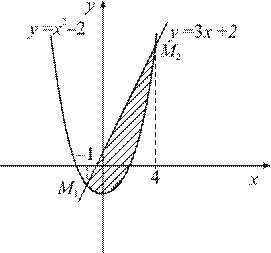
Пример.Найти площадь фигуры, ограниченной линиями:
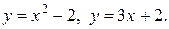
Решение. Построим схематический рисунок (рис. 2). Для построения параболы возьмем несколько точек:
| x | 0 | 1 | –1 | 2 | –2 | 3 | –3 | 4 | –4 |
| y | –2 | –1 | –1 | 2 | 2 | 7 | 7 | 14 | 14 |
Для построения прямой достаточно двух точек, например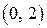 
и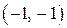 
.
Найдем координаты точек 
и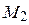 
пересечения параболы 
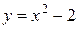и прямой 
.
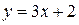Для этого решим систему уравнений
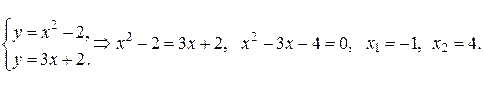
Тогда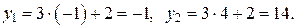 
Итак, 
Площадь полученной фигуры найдем по формуле (*), в которой
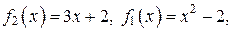поскольку 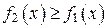для всех 
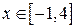. Получим:
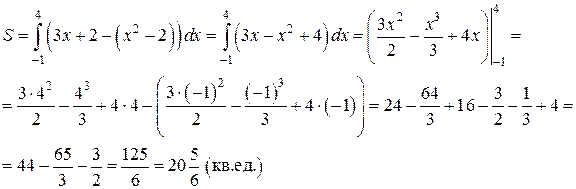
2. Вычисление площадей фигур, ограниченных линиями, заданными параметрически
Если функции 
и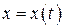 
имеют непрерывные производные первого порядка для всех 
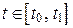, то площадь плоской фигуры, ограниченной линией 
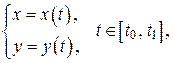прямыми x = a, x = b, где a = x(t0),
b = x(t1), и осью OX, вычисляется по формуле:
(**)
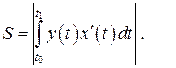Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически:
Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра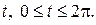 
|
|
|
| t | 0 |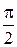 
| 
| 
| 
|
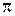
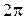
| x | 2 | 0 | –2 | 0 | 2 |
| y | 0 | 3 | 0 | –3 | 0 |
|
| Рис. 3 |
Нанесем точки (x, y) на координатную плоскость XOY и соединим плавной линией. Когда параметр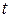 
изменяется от 
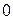до 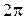, соответствующая точка 
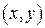описывает эллипс (известно, что 
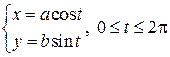— параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдем её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (9) получим:
29
Самостоятельная работа:
Задание 1. Найти площадь фигуры, ограниченной линиями, заданными параметрически.
1) 
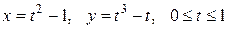
2) 
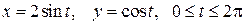
Задание 2. Составьте кроссворд по теме «Дифференциальное и интегральное исчисление» (10-15 вопросов)
Задание 3. Найти площадь фигуры, ограниченной линиями.
1) 
2) 
Содержание практического занятия:
А. Ответить на вопросы:
1) Назовите формулу, которая используется для вычисления площадей фигур в декартовой системе координат.
2) Назовите формулу, которая используется для вычисления площадей фигур, ограниченных линиями, заданными параметрически.
3) Приведите примеры нахождения площадей фигур с использованием определенного интеграла.
|
|
|
Б. Выполнить задания:
Задание 1. Найти площадь фигуры, ограниченной линиями.
1) 
2) 
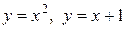
Задание 2. Найти площадь фигуры, ограниченной линиями, заданными параметрически.
1) 
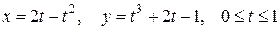
2) 
Тема: Частные производные функций нескольких переменных
Цель: сформировать умение находить частные производные функций нескольких переменных.
30
Теоретические сведения к практическому занятию:
Функция двух переменных обычно записывается как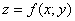 
, при этом переменные 
, 
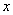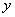называются независимыми переменными или аргументами.
Пример: 
– функция двух переменных
Обозначения:
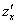или 
– частная производная по «икс»
или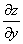 
– частная производная по «игрек»
Пример 1
Найти частные производные первого и второго порядка функции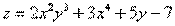 
Решение:
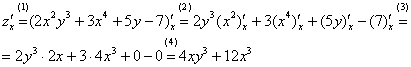
Теперь . Когда мы находим частную производную по «игрек», то переменная 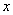считается константой (постоянным числом).
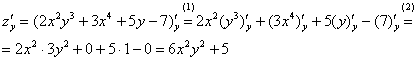
Находим частные производные второго порядка. Их четыре.
Обозначения:
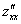или 
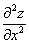– вторая производная по «икс»
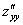или 
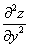– вторая производная по «игрек»
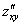или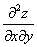 
– смешанная производная «икс по игрек»
или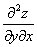 
– смешанная производная «игрек по икс»
Вторая производная – это производная от первой производной.
Для удобства я перепишу уже найденные частные производные первого порядка:
|
|
|
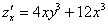
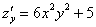
Сначала найдем смешанные производные:
Аналогично:
В практических примерах можно ориентироваться на следующее равенство:
Находим вторую производную по «икс».
Аналогично:
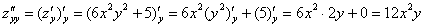
Самостоятельная работа:
Задание 1. Найти частные производные первого порядка функции двух переменных
1) 
2) 
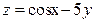
3) 
Задание 2. Найти частные производные второго порядка функции двух переменных
1) 
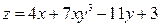
2) 
3) 
4) 
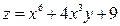
5) 
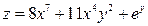
6) 
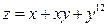
Дата добавления: 2021-04-15; просмотров: 89; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!