Ветвь 1. Попарная проверка вершин и нахождение диаметра 5 страница

а б
Рис. 2.56. Удаление вершины при декомпозиции графа
4) Вершины  и
и  смежные, но выполняется следующее неравенство
смежные, но выполняется следующее неравенство 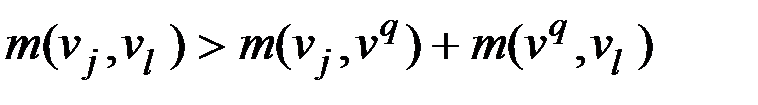 (рис. 2.57, а–г). Тогда при удалении вершины
(рис. 2.57, а–г). Тогда при удалении вершины  и инцидентных ей ребер, ребро
и инцидентных ей ребер, ребро  меняет свой весовой коэффициент на
меняет свой весовой коэффициент на
 .
.
В случае если вершины  и
и  в исходном графе
в исходном графе  смежные (в этом случае
смежные (в этом случае  ), производится присваивание
), производится присваивание  .
.
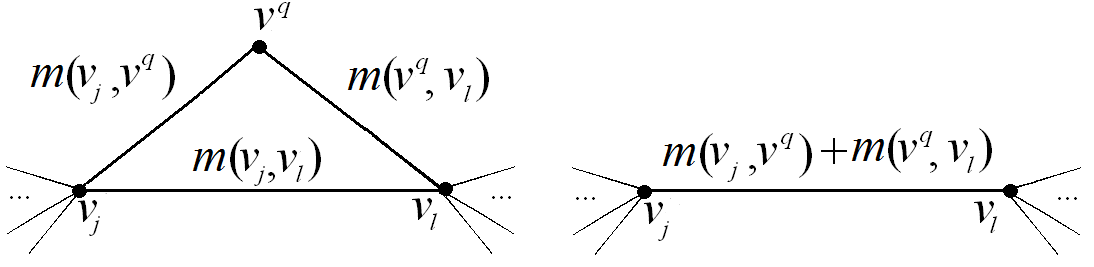
а б

в г
Рис. 2.57. Удаление вершины при декомпозиции графа:
а, б – неориентированного; в, г – ориентированного
В орграфе предыдущее относится к ситуации, когда дуги графа направлены от 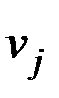 к
к 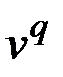 и
и  , от
, от  к
к  (рис. 2.57, в, г).
(рис. 2.57, в, г).
Если же  , то это означает, что последователем
, то это означает, что последователем 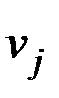 в пути
в пути 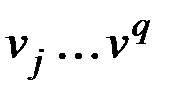 является вершина
является вершина  , то производится следующее присваивание
, то производится следующее присваивание
 .
.
Это означает, что последователем  в пути
в пути  является та же вершина, что и в пути
является та же вершина, что и в пути 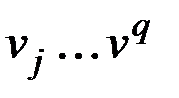 (рис. 2.58, а – г).
(рис. 2.58, а – г).

а б

в г
Рис. 2.58. Удаление вершины при декомпозиции графа
а, б – неориентированного; в, г – ориентированного
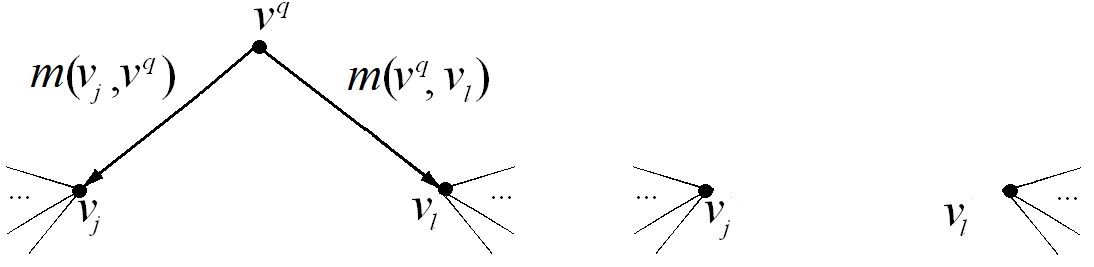
5) В случае, когда прямая дуга  отсутствует и отсутствует путь
отсутствует и отсутствует путь  (рис. 2.59), т. е. в
(рис. 2.59), т. е. в  не входит ни одна дуга, дуги, инцидентные вершине
не входит ни одна дуга, дуги, инцидентные вершине  , просто удаляются. При этом матрицы M и P не меняются.
, просто удаляются. При этом матрицы M и P не меняются.
|
|
|
а б
Рис. 2.59. Удаление вершины при декомпозиции графа
Рассмотрим более сложные случаи, которые являются комбинациями рассмотренных выше.
6) Вершина 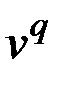 смежна с тремя несмежными вершинами
смежна с тремя несмежными вершинами 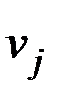 ,
,  и
и  . В этом случае
. В этом случае  удаляется с инцидентными ей ребрами, и вершины
удаляется с инцидентными ей ребрами, и вершины  ,
,  и
и  соединяются новыми ребрами с новыми весовыми коэффициентами, определяемыми следующим образом (рис. 2.60):
соединяются новыми ребрами с новыми весовыми коэффициентами, определяемыми следующим образом (рис. 2.60):
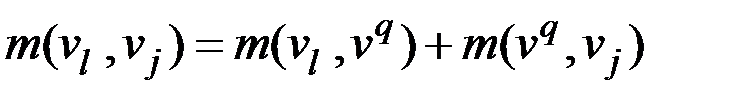 ,
,
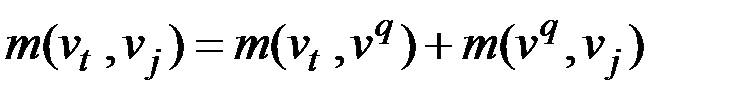 ,
,
 .
.

а б
Рис. 2.60. Удаление вершины при декомпозиции графа
7) Вершина  смежна с тремя вершинами
смежна с тремя вершинами  ,
, 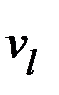 и
и 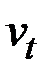 . При этом вершины
. При этом вершины  и
и  ,
,  и
и  попарно смежны. В этом случае удаление вершины
попарно смежны. В этом случае удаление вершины  и инцидентных ей ребер может не менять значения весовых коэффициентов ребер
и инцидентных ей ребер может не менять значения весовых коэффициентов ребер  ,
,  (рис. 2.61), если
(рис. 2.61), если
 ,
,
 .
.
При невыполнении какого-либо из данных неравенств соответствующее ребро приобретает новый коэффициент, равный сумме коэффициентов смежных ребер, удаленных вместе с  . Помимо того вводится новое ребро, соединяющее вершины
. Помимо того вводится новое ребро, соединяющее вершины  и
и 
|
|
|
 .
.
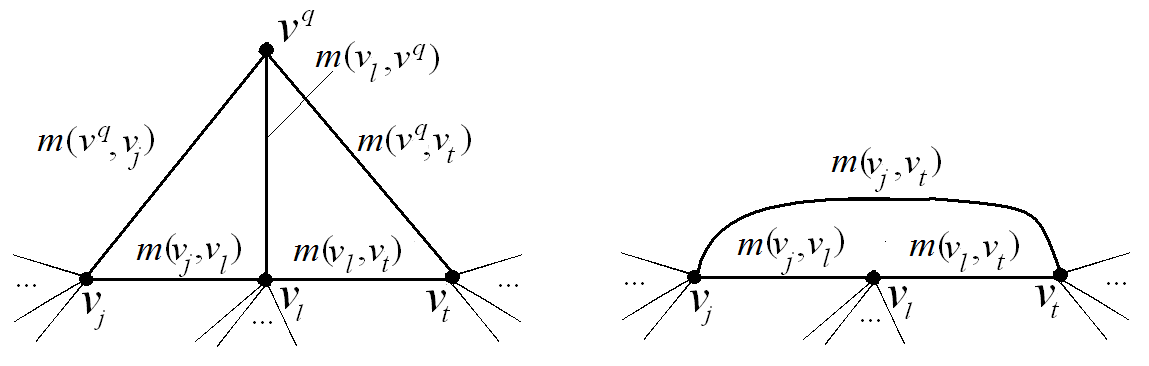
а б
Рис. 2.61. Удаление вершины при декомпозиции графа
8) Вершина  смежна с четырьмя вершинами
смежна с четырьмя вершинами  ,
,  ,
,  и
и 
(рис. 2.62, а). При этом смежны вершины:  и
и  ,
, 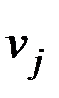 и
и  ,
,  и
и  .
.
В этом случае удаление вершины 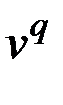 и инцидентных ей ребер формирует значения весовых коэффициентов ребер
и инцидентных ей ребер формирует значения весовых коэффициентов ребер  ,
,  ,
,  согласно предыдущему случаю (рис. 2.62, б)
согласно предыдущему случаю (рис. 2.62, б)

а

б
Рис. 2.62. Удаление вершины при декомпозиции графа
9) Вершина  смежна с четырьмя несмежными вершинами
смежна с четырьмя несмежными вершинами  ,
,  ,
,  и
и  (рис. 2.63). Вершина
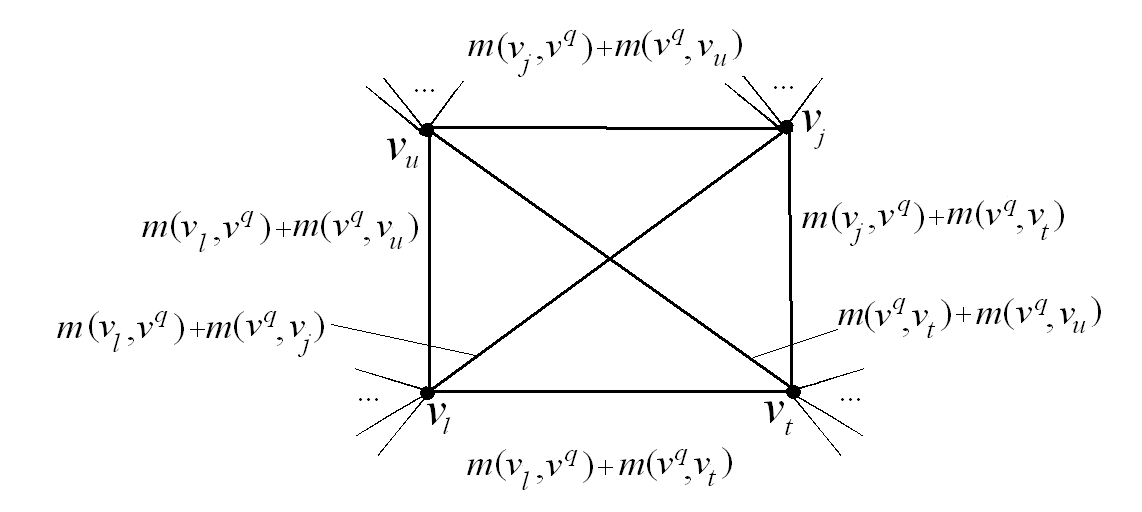
(рис. 2.63). Вершина  и инцидентные ей ребра удаляются, при этом оставшиеся вершины соединяются новыми ребрами с новыми весовыми коэффициентами, определяемыми следующим образом:
и инцидентные ей ребра удаляются, при этом оставшиеся вершины соединяются новыми ребрами с новыми весовыми коэффициентами, определяемыми следующим образом:
 ,
,
 ,
,
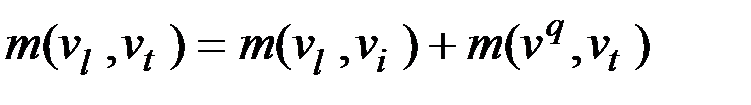 ,
,
 ,
,
 ,
,
 .
.

а
б
Рис. 2.63. Удаление вершины при декомпозиции графа
Таким образом, алгоритм формирования матриц 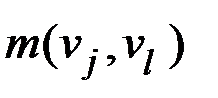 ,
, 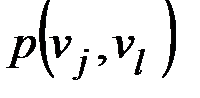 размерности
размерности  может быть представлен в следующем виде.
может быть представлен в следующем виде.
В начале алгоритма элементы матриц равны  ,
,  (или
(или  , если
, если  ).
).
Пусть на шаге q удаляется вершина  . Для сохранения информации о путях на каждом шаге q этапа разборки графа элементы матриц пересчитываются. Для этого рассматриваются все пары вершин, смежных с удаляемой (
. Для сохранения информации о путях на каждом шаге q этапа разборки графа элементы матриц пересчитываются. Для этого рассматриваются все пары вершин, смежных с удаляемой (  ).
).
|
|
|
Если выполняются условия  и
и 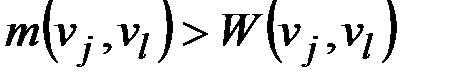 , то
, то
 , (2.29)
, (2.29)
 . (2.30)
. (2.30)
Если  и
и  , то это означает, что дуга
, то это означает, что дуга  графа
графа  состоит из двух или более дуг исходного графа
состоит из двух или более дуг исходного графа  . Если условия выполнения операций (2.29), (2.30) не выполняются, то значения
. Если условия выполнения операций (2.29), (2.30) не выполняются, то значения  и
и  остаются равными значениям на предыдущем шаге разборки.
остаются равными значениям на предыдущем шаге разборки.
Процесс разборки продолжается, пока в графе не останутся только две вершины при  . При этом, как будет доказано ниже, в графе
. При этом, как будет доказано ниже, в графе  найдены кратчайшие пути между этими двумя вершинами.
найдены кратчайшие пути между этими двумя вершинами.
Разборку графа можно представить в виде следующей блок-схемы (рис. 2.64).

Рис. 2.64. Блок-схема алгоритма разборки графа
Микрорешение
В результате разборки остается подграф Gr. Если производится полная разборка исходного графа и в Gr остаются две вершины, на данном этапе в матрицах М и P ничего не меняется. Если полученный подграф Gr содержит более двух вершин, необходимо найти оптимальные пути между всеми парами его вершин. Результатом решения задачи APSP на подграфе Gr является матрица расстояний Mr. Элементы матрицы расстояний M для вершин  из подграфа Gr изменяются по формуле
из подграфа Gr изменяются по формуле  и производится изменение матрицы P по формулам
и производится изменение матрицы P по формулам
|
|
|


где  – элементы матрицы последователей Pr подграфа Gr. Найденные на этом этапе пути между вершинами графа Gr будут гарантированно кратчайшими.
– элементы матрицы последователей Pr подграфа Gr. Найденные на этом этапе пути между вершинами графа Gr будут гарантированно кратчайшими.
Сборка графа
До начала работы данного этапа алгоритма определена последовательность графов  , последовательность удаленных вершин
, последовательность удаленных вершин 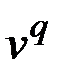 ,
,  и соответствующие множества
и соответствующие множества  ,
,  . Здесь
. Здесь  – исходный граф,
– исходный граф, 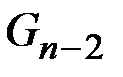 – последний граф последовательности, в котором найдены кратчайшие пути между вершинами. На этапе сборки производится обратный ход от
– последний граф последовательности, в котором найдены кратчайшие пути между вершинами. На этапе сборки производится обратный ход от  к
к  через графы
через графы 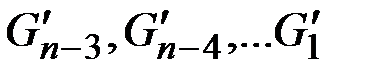 с расчетом кратчайших путей на каждом шаге
с расчетом кратчайших путей на каждом шаге  между вершинами
между вершинами  и
и  . В графе
. В графе  определены кратчайшие пути, поэтому при добавлении вершины
определены кратчайшие пути, поэтому при добавлении вершины 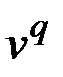 и определении кратчайших путей между
и определении кратчайших путей между 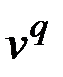 и
и  минимум выбирается между длиной прямого пути
минимум выбирается между длиной прямого пути  за один шаг и длинами путей за два шага
за один шаг и длинами путей за два шага  ,
,  ,
, 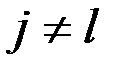 . Пути, состоящие из большего числа шагов
. Пути, состоящие из большего числа шагов  , проходящие через другие вершины графа
, проходящие через другие вершины графа  , не рассматриваются, так как их длина не минимальна (по крайней мере, их длина не меньше, чем длина
, не рассматриваются, так как их длина не минимальна (по крайней мере, их длина не меньше, чем длина  ).
).
Минимальные расстояния от  до любой вершины
до любой вершины  графа
графа  можно рассчитать по следующим формулам. Пусть
можно рассчитать по следующим формулам. Пусть
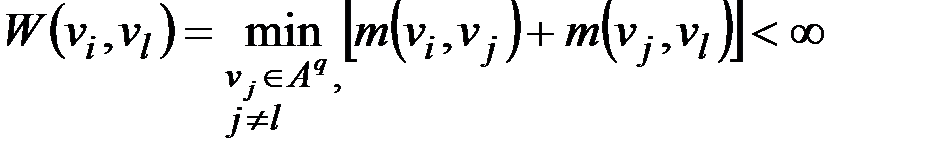 (2.31)
(2.31)
Дата добавления: 2021-02-10; просмотров: 76; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
