Ветвь 1. Попарная проверка вершин и нахождение диаметра 7 страница
Рис. 2.66. Пример неориентированного нагруженного графа
Дана матрица его весов, необходимо найти минимальные пути между каждой парой вершин. На начальном этапе множество 
содержит все вершины графа 
.
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
В начале матрица кратчайших расстояний 
совпадает с матрицей длин ребер. Также вводится матрица последователей P, в которой указываются вершины, следующие за вершиной, соответствующей номеру строки в минимальном пути. Вначале в матрицу последователей P записываются информация о ребрах графа.
Разборка графа
1) На первом этапе выбираем вершину наименьшей степени (если их несколько, то с меньшим порядковым номером). В данном случае 
(ее степень 2). Имеем множества 
и 
. Пересчитываем значения весовых коэффициентов ребер, связывающих вершины из 
:
.
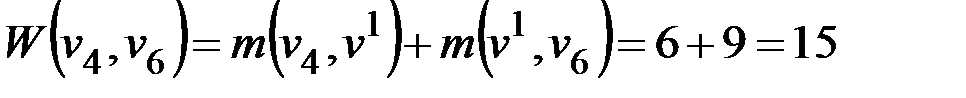Поскольку ребра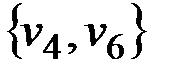 
нет, вводим данное ребро с весом 15, т. е. 
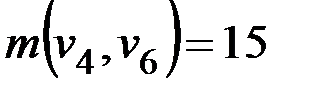. При этом получаем граф 
(рис. 2.67).
В матрице P в ячейки 
и 
заносится значение 
, так как вершина 
– последователь вершины 
в пути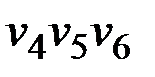 
и вершины 
в пути 
. В матрицу кратчайших расстояний в ячейки 
и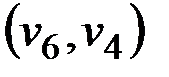 
вносится рассчитанное значение 15.
|
|
|
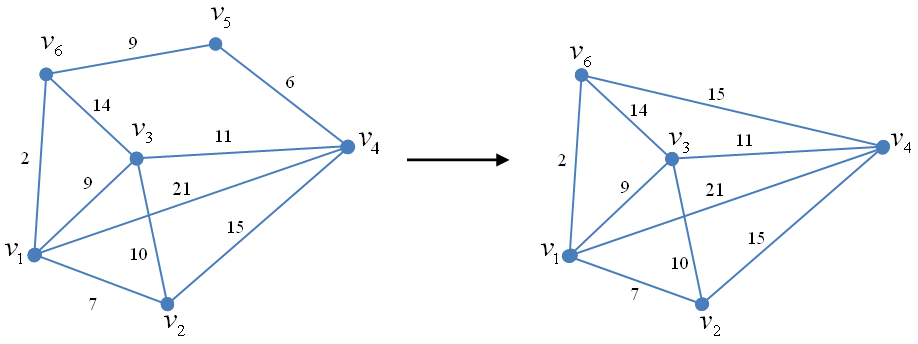
а б
Рис. 2.67. Пример разборки неориентированного нагруженного графа. Шаг 1;
а – граф G0; б – граф G1
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2) Удаляем следующую вершину наименьшей степени, теперь это 
, т. е.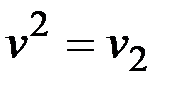 
. Тогда множество 
и 
. Пересчитываем значения весовых коэффициентов ребер, связывающих вершины из 
:
;
;
.
Поскольку ребро 
имеет весовой коэффициент, меньший, чем 
, оставляем его весовой коэффициент без изменения. По той же причине сохраняем весовые коэффициенты ребер 
и 
. Поэтому в матрицы P и M не вносится никаких изменений. При этом получаем граф 
(рис. 2.68).
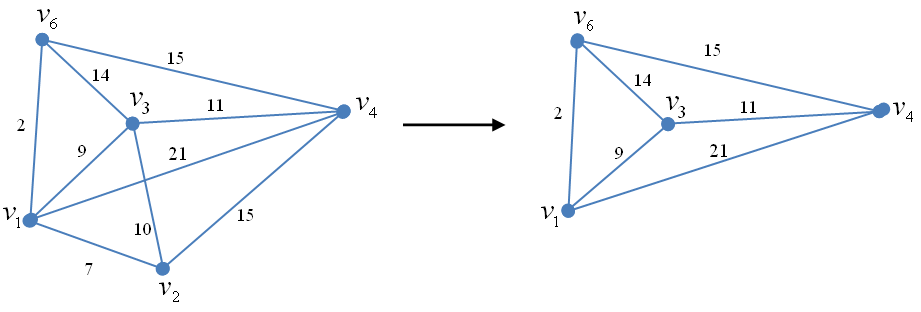
а б
|
|
|
Рис. 2.68. Пример разборки неориентированного нагруженного графа. Шаг 2;
а – граф G1; б – граф G2
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3) Удаляем следующую вершину наименьшей степени, 
. Тогда множество 
и 
. Пересчитываем значения весовых коэффициентов ребер, связывающих вершины из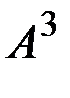 
:
;
;
.
Ребро 
, в отличие от 
и 
, имеет весовой коэффициент, превышающий 
, поэтому заменяем его весовой коэффициент на значение 
, т. е. 
. Получаем граф 
(рис. 2.69).
а б
Рис. 2.69. Пример разборки неориентированного нагруженного графа. Шаг 3;
а – граф G2; б – граф G3
При этом в матрице P в ячейках 
и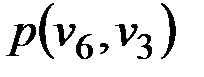 
значения v6и v3 заменяются на 
, как предполагаемый последователь вершины 
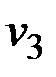в пути 
и вершины 
в пути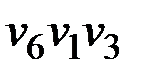 
.
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4) Удаляем вершину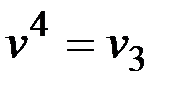 
. 
. Пересчитываем значения весовых коэффициентов ребер, связывающих вершины из 
:
.
Поскольку ребро 
имеет весовой коэффициент, меньший, чем 
, оставляем без изменения обе матрицы. При этом получаем граф 
(рис. 2.70).
а б
Рис. 2.70. Пример разборки неориентированного нагруженного графа. Шаг 4;
Дата добавления: 2021-02-10; просмотров: 78; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!