Ветвь 1. Попарная проверка вершин и нахождение диаметра 4 страница

;

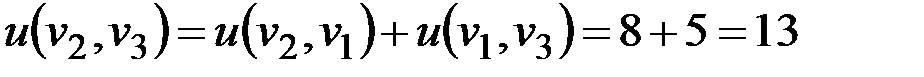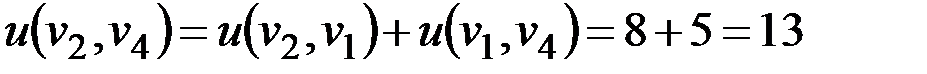Изменяем погрешность, вносимую вершиной v₃: 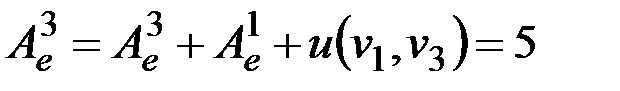. Граф приобретает вид, изображенный на рис. 2.48.

Следующая рассматриваемая вершина v₂. Это вершина может быть аппроксимирована v₄, так как . Удаляем вершину v₂, пересчитываем вес ребра только между вершинами v₄,v₆, так как веса ребер между v₄,v₃, и v₆,v₃ меньше длин путей через v₂.

Изменяем погрешность, вносимую вершиной v₄: . Граф приобретает вид, изображенный на рис. 2.49.

Следующая рассматриваемая вершина v₈. Это вершина может быть аппроксимирована v₆, так как 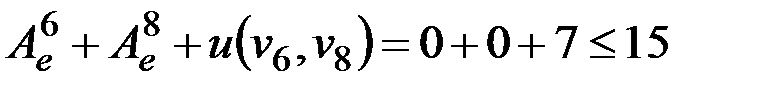. Удаляем вершину v₈, пересчитываем вес ребра только между вершинами v₆,v₉, так как веса ребер между v₆,v₇, и v₇,v₉ меньше длин путей через v₈.

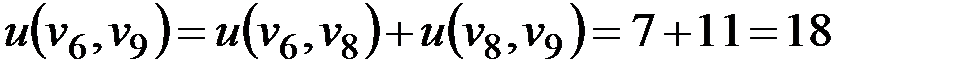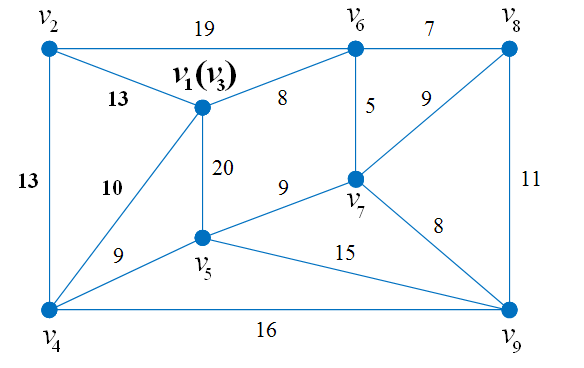
Рис. 2.48. Граф после первой итерации алгоритма

Рис. 2.49. Граф после второй итерации алгоритма

Изменяем погрешность, вносимую вершиной v₆: . Граф приобретает вид, изображенный на рис. 2.50.

Рис. 2.50. Граф после третьей итерации алгоритма

Следующая рассматриваемая вершина v₇. Это вершина может быть аппроксимирована v₆, так как 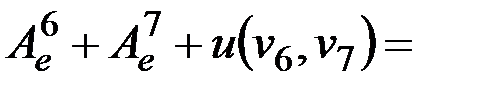. Удаляем вершину v₇, пересчитываем веса ребер между вершинами v₅,v₆ и v₆,v₉, так как вес ребра между v₅,v₉ меньше длины пути через v₇.

;

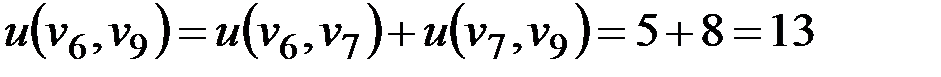Изменяем погрешность, вносимую вершиной v₆: 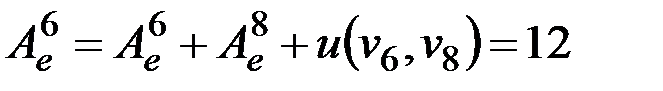. Граф приобретает вид, изображенный на рис. 2.51.

Рис. 2.51. Граф после четвертой итерации алгоритма

Следующая рассматриваемая вершина v₉. Это вершина может быть аппроксимирована v₅, так как . Удаляем вершину v₉, пересчитываем вес ребра между вершинами v₄,v₆, так как веса ребер между v₄,v₅, и v₅,v₆ меньше длин путей через v₉.

Изменяем погрешность, вносимую вершиной v₅: 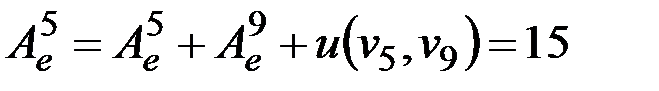. Граф приобретает вид, изображенный на рис. 2.52.

Дальнейшее удаление вершин невозможно, так как будет нарушено условие (2.28). Подграф исходного графа G, образуемый метавершиной v₄(v₂) полученного аппроксимирующего графа не является связным (рис. 2.47). Перенос вершины v₂ в множество v₃(v₁) увеличивает радиус множества r(v₃(v₁)) = 5 на 3 (m(v₁, v₂) = 8). Следовательно, вершина v₁ переносится в множество v₄(v₂) формируя связную относительно исходного графа метавершину v₄(v₂, v₁). Получившийся аппроксимирующий подграф изображен на рис. 2.53.

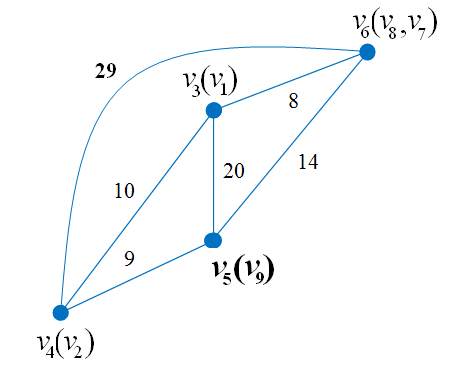
Рис. 2.52. Граф после пятой итерации алгоритма

Рис. 2.53. Полученный аппроксимирующий граф

Таким образом, получен аппроксимирующий граф, содержащий четыре вершины с фактической погрешностью аппроксимации, согласно табл. 2.1 и 2.2, A_e = 20 < e_max = 30, достигаемой на паре вершин v₂, v₉.

Таблица 2.1.

Матрица расстояний исходного графа G

m(v_i_, v_j)	v₁	v₂	v₃	v₄	v₅	v₆	v₇	v₈	v₉
v₁	0	8	5	5	14	13	18	20	21
v₂	8	0	13	13	22	19	24	26	29
v₃	5	13	0	10	19	8	13	15	21
v₄	5	13	10	0	9	18	18	25	16
v₅	14	22	19	9	0	14	9	18	15
v₆	13	19	8	18	14	0	5	7	13
v₇	18	24	13	18	9	5	0	9	8
v₈	20	26	15	25	18	7	9	0	11
v₉	21	29	21	16	15	13	8	11	0

Таблица 2.2.

Матрица расстояний вершин исходного графа G

согласно полученной аппроксимации

m(v_i_, v_j)	v₁	v₂	v₃	v₄	v₅	v₆	v₇	v₈	v₉
v₁	0	4	10	4	9	18	18	18	9
v₂	4	0	10	4	9	18	18	18	9
v₃	0	10	0	10	19	8	8	8	19
v₄	4	4	10	0	9	18	18	18	9
v₅	9	9	19	9	0	14	14	14	7,5
v₆	18	18	8	18	14	0	3,5	3,5	14
v₇	18	18	8	18	14	3,5	0	3,5	14
v₈	18	18	8	18	14	3,5	3,5	0	14
v₉	9	9	19	9	7,5	14	14	14	0

2.7.5. Задача поиска оптимальных путей между всеми парами узлов транспортной сети

Для разреженных графов предлагается алгоритм «разборки-сборки графа». На этапе разборки из графа последовательно удаляются вершины, далее производится поиск решения на малом графе, после чего исходный граф собирается с получением искомых кратчайших расстояний. Отличие предлагаемого алгоритма от уже известных алгоритмов со сжатием или подменой ребер (shortcut) состоит в том, что он достаточно прост, выполняет расчет кратчайших путей сразу между всеми вершинами, при этом гарантированно находит точное решение (не является эвристическим).

Алгоритм разборки-сборки графа транспортной сети

Дан связный ориентированный или неориентированный разреженный простой нагруженный граф 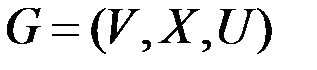с неотрицательной вещественной весовой функцией на ребрах U: . Необходимо для всех пар вершин графа найти кратчайший путь между вершинами в паре, т. е. найти матрицу расстояний M и матрицу последователей P.

Пусть 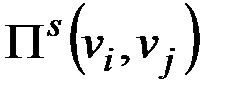– кратчайший путь в графе G.

& Определение. Матрица последователей – матрица размерности , элемент 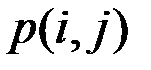которой представляет собой идентификатор вершины, которая следует за вершиной в кратчайшем пути от и . То есть элементы матрицы P определяются по формуле

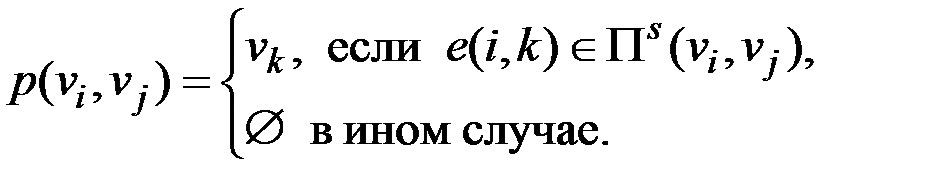
Общая идея алгоритма поиска решения

Принцип предлагаемого алгоритма состоит в сведении задачи на исходном графе большой размерности к задаче на графе малой размерности. Алгоритм можно разделить на три этапа:

Разборка (декомпозиция) – замена исходного графа графом меньшей размерности.

Микрорешение – решение задачи о кратчайших путях на графе меньшей размерности с использованием существующих методов.

Сборка – перенос решения с графа меньшей размерности на исходный граф; пересчет кратчайших расстояний для части вершин исходного графа.

Такой подход требует выполнения следующих условий:

а) достоверность – сжатие должно сохранять информацию о кратчайших путях исходного графа;

б) скорость – выполнение всех этапов в сумме должно требовать меньше времени, чем решение задачи известными способами на исходном графе.

Рассмотрим граф . Обозначим через и будем называть сжимающей последовательность графов , где ; 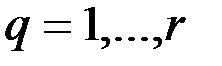. Каждый следующий граф последовательности получается из предыдущего 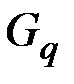удалением одной (или нескольких) вершин и инцидентных им ребер, добавлением новых ребер и пересчетом весов ребер между вершинами, смежными с удаленными. Для таких графов справедливо , .

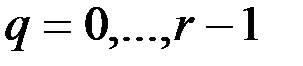Разборка графа

Этап разборки графа является многоступенчатым и состоит в последовательном приближении исходного графа 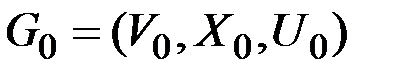графами сжимающей 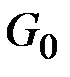последовательности .

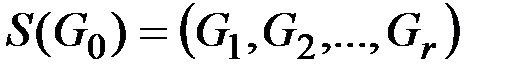Сначала рассмотрим случай, когда каждый следующий граф последовательности 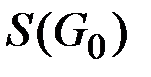получается из предыдущего графа удалением одной вершины , .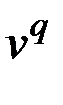

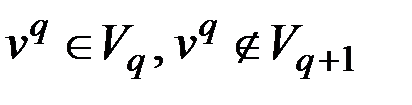Обозначим 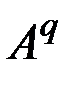– множество всех смежных с вершин в графе с номерами .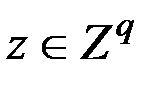

Зададим начальные значения матрицы M и P. Вначале задаются значения

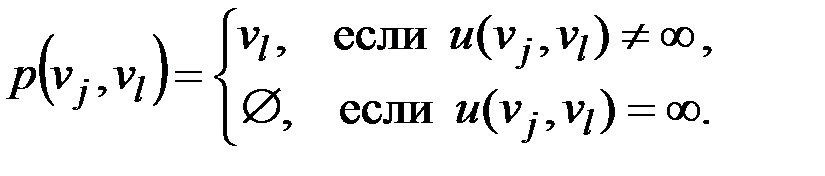
Пусть удаляемая вершина графа 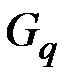имеет степень k и с ней смежны вершины , 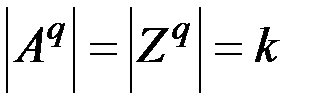. Если какой-то из кратчайших путей графа проходит через вершину (не считая путей, начинающихся с 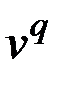или заканчивающихся вершиной ), то этот путь обязательно содержит подпуть вида 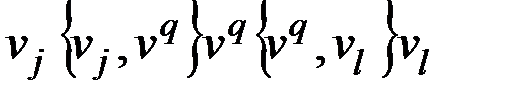для некоторых . Таким образом, при удалении вершины необходимо гарантировать сохранение кратчайших путей только между вершинами, смежными с .

В связи с этим возможны различные случаи преобразования исходного графа. Наиболее частые из них приведены ниже.

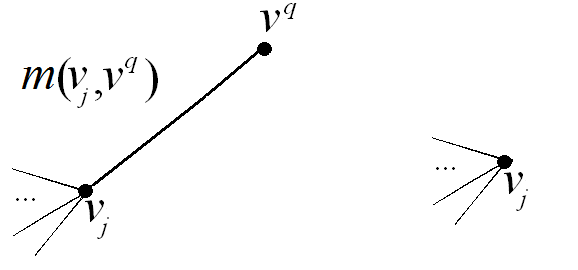
1) Вершина имеет степень единицу, т. е. смежна только с одной вершиной графа G _q. Тогда сохранять кратчайшие пути надобности нет (так как через они не проходят), и в этом случае вершина 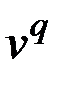и инцидентное ей ребро просто удаляются из графа (рис. 2.54). Матрицы M и P не меняются.

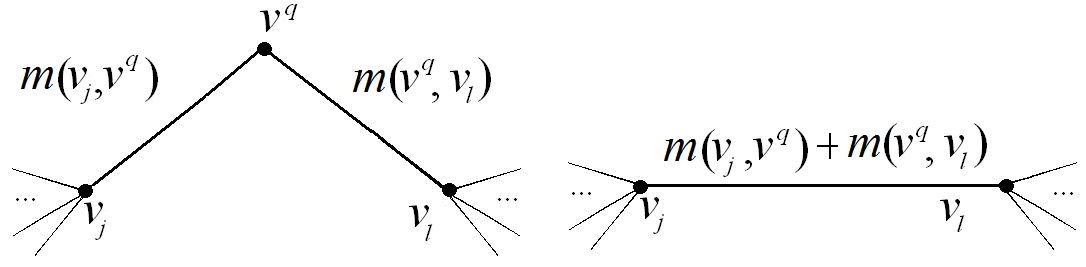
2) Вершины 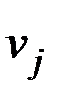и не смежные (рис. 2.55). Тогда при удалении вершины 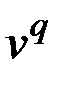и инцидентных ей ребер с весовыми коэффициентам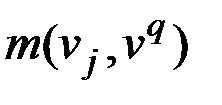и и 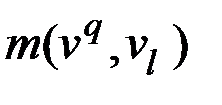вводится ребро с весовым коэффициентом

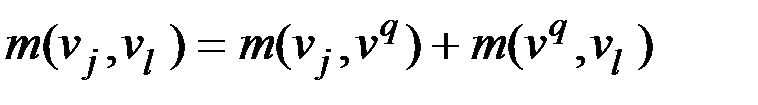В матрице P .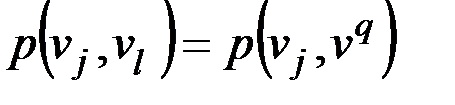

а б

Рис. 2.54. Удаление вершины при декомпозиции графа

а б

Рис. 2.55. Удаление вершины при декомпозиции графа

3) Вершины и 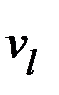смежные, при этом выполняется неравенство (рис. 2.56). Тогда при удалении вершины и инцидентных ей ребер, ребро сохраняет свой весовой коэффициент. Матрицы M и P не меняются.

Дата добавления: 2021-02-10; просмотров: 71; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!