Ветвь 1. Попарная проверка вершин и нахождение диаметра 2 страница

=  заменяется на 17, = = 14 заменяется на меньшее 11.

Вычисляем эксцентриситет претендента ε(c₁) = 17. Так как , полагаем . Верхняя и нижняя границы радиуса не равны: , значит, вершина c₁ = v₃ не является центральной.

Находим самую удаленную от c₁ вершину: v₅ с расстоянием . Так как для v₅ не найдены все кратчайшие пути, решаем SSSP(v₅) и добавляем v₅ в множество опорных вершин: . При этом матрица длин ребер изменяется следующим образом: =  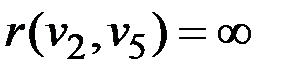заменяется на 18.

 

	v1	v2	v3	v4	v5	v6
v1	0	7	9	17	11	2
v2	7	0	10	15	18	∞
v3	9	10	0	11	17	11
v4	17	15	11	0	6	15
v5	11	18	17	6	0	9
v6	2	∞	11	15	9	0

 

Находим следующего претендента c₂ – это вершина v₆ с . Согласно формуле (2.2) изменяем нижнюю границу радиуса, полагая r_l = 15. Для c₂ кратчайшие расстояния не найдены, решаем SSSP(c₂ = v₆), в матрице длин ребер при этом значение =  заменяется на 9.

 

	v1	v2	v3	v4	v5	v6
v1	0	7	9	17	11	2
v2	7	0	10	15	18	9
v3	9	10	0	11	17	11
v4	17	15	11	0	6	15
v5	11	18	17	6	0	9
v6	2	9	11	15	9	0

 

Вычисляем эксцентриситет претендента ε(c₂) = 15. Так как , полагаем . В данном случае нижняя и верхние границы совпадают 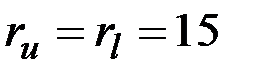, значит, вершина c₂ = v₆ является центральной, при этом радиус графа равен .

Таким образом, найден центр графа (в данном случае центр состоит из одной вершины) и его радиус. При этом задача SSSP решена для 5 вершин, против 6 решений SSSP при поиске радиуса обычным способом. В данном примере коэффициент уменьшения числа решений SSSP разработанным алгоритмом составил 5/6, однако на реальных графах большой размерности, как показывают эксперименты, этот показатель значительно ниже – до 1% и менее.

Теперь найдем диаметр графа, используя алгоритм Д1. Для начальной оценки нижней d_l и верхней d_u границ диаметра используется информация о кратчайших расстояниях от вершин, для которых решена задача SSSP во время поиска радиуса. В данном примере таких вершин пять: v₁, v₃, v₄, v₅ и v₆. Обходим эти вершины по порядку и итерационно уточняем значения нижней и верхней границ диаметра, а также исключаем из рассмотрения вершины, чей эксцентриситет удовлетворяет условиям (2.11), (2.12).

Изначально , , матрица границ эксцентриситетов вершин имеет вид

 

	v1	v2	v3	v4	v5	v6
εl	–∞	–∞	–∞	–∞	–∞	–∞
εu	∞	∞	∞	∞	∞	∞

Рассматриваем вершину v₁. Получаем значения нижней и верхней границ диаметра:

, .

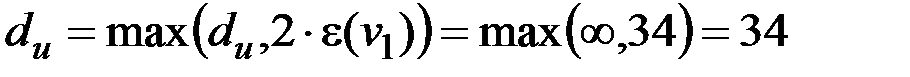Вычисляем нижние и верхние границы эксцентриситетов вершин:

ε_l(v₁) = max(ε_l(v₁), ε(v₁) – , 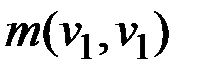) = max(–∞, 17 – 0, 0) = 17;

ε_u(v₁) = min(ε_u(v₁), ε(v₁) + ) = min(∞, 17 + 0) = 17;

ε_l(v₂) = max(ε_l(v₂), ε(v₁) – , ) = max(–∞, 17 – 7, 7) = 10;

ε_u(v₂) = min(ε_u(v₂), ε(v₁) + ) = min(∞, 17 + 7) = 24;

ε_l(v₃) = max(ε_l(v₃), ε(v₁) – , ) = max(–∞, 17 – 9, 9) = 9;

ε_u(v₃) = min(ε_u(v₃), ε(v₁) + 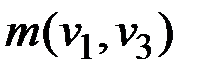) = min(∞, 17 + 9) = 26;

ε_l(v₄) = max(ε_l(v₄), ε(v₁) – ,

) = max(–∞, 17 – 17, 17) = 17;

ε_u(v₄) = min(ε_u(v₄), ε(v₁) + ) = min(∞, 17 + 17) = 34;

ε_l(v₅) = max(ε_l(v₅), ε(v₁) – ,

) = max(–∞, 17 – 11, 11) = 11;

ε_u(v₅) = min(ε_u(v₅), ε(v₁) + ) = min(∞, 17 + 11) = 28;

ε_l(v₆) = max(ε_l(v₆), ε(v₁) – , 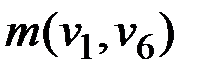) = max(–∞, 17 – 2, 2) = 15;

ε_u(v₆) = min(ε_u(v₆), ε(v₁) + ) = min(∞, 17 + 2) = 19.

Из рассмотрения при этом исключаются вершины v₁ и v₄, так как ε_l(v₁) = ε_u(v₁) и ε_l(v₄) = d_u/2. Матрица границ эксцентриситетов принимает вид

 

	v1	v2	v3	v4	v5	v6
εl	17	10	9	17	11	15
εu	17	24	26	34	28	19

 

Далее рассматриваем вершину v₃. Эксцентриситет вершины v₃ не изменяет значений нижней и верхней границ диаметра: d_l = max(d_l,ε(v₃)) = (17, 17) = 17, d_u = min(d_u,2∙ε(v₃)) = (34, 34) = 34. Уточняем нижние и верхние границы эксцентриситетов не исключенных вершин:

ε_l(v₂) = max(ε_l(v₂), ε(v₃) – ,

) = max(10, 17 – 10, 10) = 10;

ε_u(v₂) = min(ε_u(v₂), ε(v₃) + ) = min(24, 17 + 10) = 24;

ε_l(v₃) = max(ε_l(v₃), ε(v₃) – 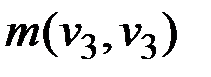, ) = max(9, 17 – 17, 17) = 17;

ε_u(v₃) = min(ε_u(v₃), ε(v₃) + 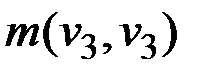) = min(26, 17 + 0) = 17;

ε_l(v₅) = max(ε_l(v₅), ε(v₃) – ,

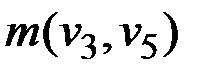) = max(11, 17 – 17, 17) = 17;

ε_u(v₅) = min(ε_u(v₅), ε(v₃) + ) = min(28, 17 + 17) = 28;

ε_l(v₆) = max(ε_l(v₆), ε(v₃) – ,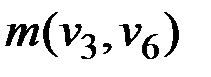

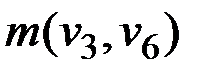) = max(15, 17 – 11, 11) = 15;

ε_u(v₆) = min(ε_u(v₆), ε(v₃) + 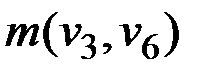) = min(19, 17 + 11) = 19.

Из рассмотрения при этом исключаются вершины v₃ и v₅, так как ε_l(v₃) = ε_u(v₃) и ε_l(v₅) = d_u/2. Матрица границ эксцентриситетов принимает вид

 

	v1	v2	v3	v4	v5	v6
εl	17	10	17	17	17	15
εu	17	24	17	34	28	19

 

Теперь рассматриваем вершину v₄. Эксцентриситет вершины v₄ не изменяет значений нижней и верхней границ диаметра: d_l = max(d_l, ε(v₄)) = (17, 17)=17, d_u = min(d_u, 2∙ε(v₄)) = (34, 34) = 34. Уточняем нижние и верхние границы эксцентриситетов не исключенных вершин:

ε_l(v₂) = max(ε_l(v₂), ε(v₄) – ,

) = max(10, 17 – 15, 15) = 15;

ε_u(v₂) = min(ε_u(v₂), ε(v₄) + ) = min(24, 17+15) = 24;

ε_l(v₆) = max(ε_l(v₆), ε(v₄) – ,

) = max(15, 17 – 15, 15) = 15;

ε_u(v₆) = min(ε_u(v₆), ε(v₄) + ) = min(19, 17 + 15) = 19.

Ни одна из оставшихся вершин не исключаются из рассмотрения. Матрица границ эксцентриситетов принимает вид

 

	v1	v2	v3	v4	v5	v6
εl	17	15	17	17	17	15
εu	17	24	17	34	28	19

 

Далее рассматриваем вершину v₅. Значение нижней границы диаметра изменяется: d_l = max(d_l, ε(v₅)) = (17, 18) = 18, а верхней – нет: d_u = min(d_u, 2∙ε(v₅)) = (34, 36) = 34. Уточняем нижние и верхние границы эксцентриситетов неисключенных вершин:

ε_l(v₂) = max(ε_l(v₂), ε(v₅) – ,

) = max(15, 17 – 18, 18) = 18;

ε_u(v₂) = min(ε_u(v₂), ε(v₅) + ) = min(24, 17 + 18) = 24;

ε_l(v₆) = max(ε_l(v₆), ε(v₅) – , ) = max(15, 17 – 9, 9) = 15;

ε_u(v₆) = min(ε_u(v₆), ε(v₅) + 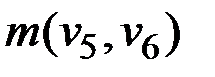) = min(19, 17 + 9) = 19.

Из рассмотрения при этом исключается вершина v₂, так как 18 = ε_l(v₂) > d_u/2 = 17. Матрица границ эксцентриситетов принимает вид

 

	v1	v2	v3	v4	v5	v6
εl	17	18	17	17	17	15
εu	17	24	17	34	28	19

 

---

Дата добавления: 2021-02-10; просмотров: 72; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!