Выделение компонент сильной связности орграфа
ТеориЯ графов
2.1. Общие понятия теории графов
Теория графов – это математический аппарат, применяемый для формализации (моделирования) реальных задач по исследованию свойств конечных множеств с заданными отношениями между их элементами. В их числе задачи из области администрирования сетей, информационных потоков, планирования, проектирования и управления различными системами.
& Определение. Графом 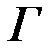 называется любая пара
называется любая пара 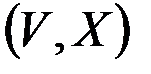 , где
, где  – множество элементов произвольной природы, называемых вершинами графа;
– множество элементов произвольной природы, называемых вершинами графа; 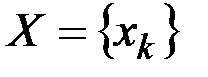 (k=1,...,m) – семейство пар из
(k=1,...,m) – семейство пар из 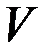 :
: 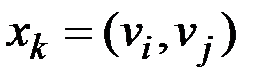 (i, j=1,...,n).
(i, j=1,...,n).
Задачи на графах удобно переводить на языки программирования, т. е. решать с использованием современной вычислительной техники.
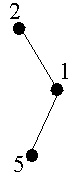
Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис.2.1, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.
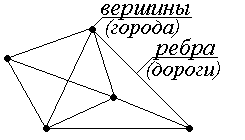
Рис. 2.1. Пример графа
Широкое определение графа допускает любую трактовку: множество предприятий с экономическими отношениями, множество людей с психологической совместимостью, система управления с подчинением, технические системы со связями, электрические цепи с источниками и потребителями, транспортные сети. Поэтому язык теории графов получил распространение в химии, физике, лингвистике, экономике, психологии и т.д.
|
|
|
& Определение. Неориентированным г рафом G = (V, X) называется пара множеств: V – множество, элементы которого называются вершинами, X – множество неупорядоченных пар вершин, называемых ребрами.
Если вершины v, wÎV, x=(v,w)ÎX, то говорят, что ребро x соединяет вершины v и w или x инцидентно v и w. Таким образом, {v, w} – обозначение ребра.
Если Х представляет собой упорядоченные пары (т. е. X – подмножество декартова произведения V × V), то граф называется ориентированным (орграфом), а пары (v, w) называют дугами.
? Замечание. Граф, в котором присутствуют и ребра и дуги называется смешанным. Записывается упорядоченной тройкой G=(V, X, A), где V – множество вершин, X – множество ребер и A – множество дуг. Очевидно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Если множеству X принадлежат пары v=w, то такие ребра {v, v} (дуги (v, w)) называют петлями.
Существование одинаковых пар {v, w} (или (v, w)) соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер (дуг) называют количество таких одинаковых пар.
Пример
v Кратность ребра {v1, v2} в графе на рис.2.2 равна двум, кратность ребра {v3, v4} − трем.
|
|
|
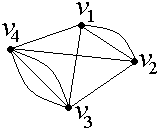
Рис. 2.2. Пример графа с кратными ребрами
& Определения
Псевдограф – граф, в котором есть петли и/или кратные ребра.
Мультиграф – псевдограф без петель.
Простой граф – граф без кратных ребер и петель.
Граф, состоящий из одной вершины, называется тривиальным.
Будем применять следующие обозначения:
V – множество вершин;
X – множество ребер или дуг;
v (или vi) – вершина;
G – неориентированный граф;
D – орграф;
{v, w} – ребро неориентированного графа;
(v, w) – дуга в орграфе;
{v, v}, (v, v) – обозначение петли;
x, y, z – ребра и дуги;
n(G), n(D), 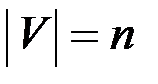 – мощность множества вершин графа;
– мощность множества вершин графа;
m(G) (m(D)), 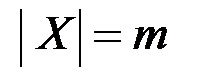 – мощность множества ребер (дуг).
– мощность множества ребер (дуг).
Примеры
v Орграф D=(V, X) (рис. 2.3), V={v1, v2, v3, v4},
X={x1=(v1, v2), x2=(v1, v2), x3=(v2, v2), x4=(v2, v3)}.

Рис. 2.3. Пример орграфа
v3 – висячая вершина, v4 – изолированная вершина
v Неориентированный граф (рис.2.4):
G=(V, X), V={v1, v2, v3, v4, v5},
X={x1={v1, v2}, x2={v2, v3}, x3={v2, v4}, x4={v3, v4}}.
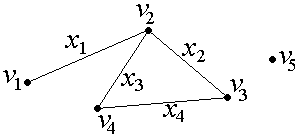
Рис. 2.4. Пример неориентированного графа
v1 – висячая вершина, v5 – изолированная вершина
& Определения
Если x={v, w} – ребро, то v и w − концы ребра x.
Если x=(v, w) – дуга орграфа, то v − начало, w – конец дуги.
Вершина v и ребро x неориентированного графа (дуга x орграфа) называются инцидентными, если v является концом ребра x (началом или концом дуги x).
|
|
|
Вершины v, w называются смежными, если {v, w}ÎX.
Ребра называются смежными, если они инцидентны одной и той же вершине.
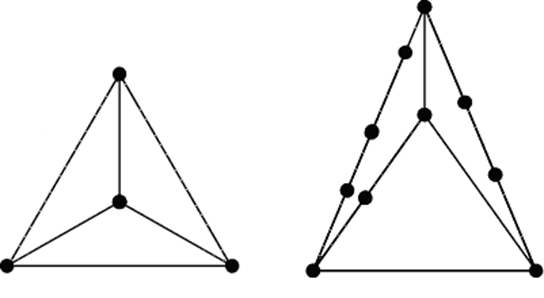
& Определение. П олный граф – это простой граф, в котором любые две вершины смежные, обозначается Kn, где n – число вершин.
? Замечание. Число ребер полного неориентированного графа 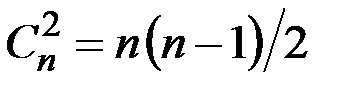 .
.
На рис. 2.5 показаны неориентированные полные графы и их число ребер.
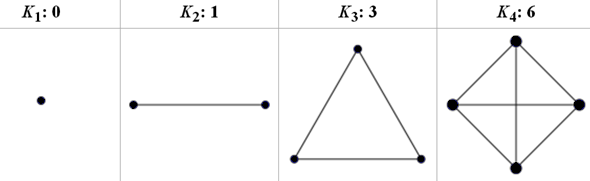
Рис. 2.5. Полные графы K1, K2, K3 и K4
& Определение. Степенью вершины v графа G называется число d(v) ребер графа G, инцидентных вершине v.
Вершина графа, имеющая степень 0, называется изолированной, а степень 1 – висячей (рис.2.3, 2.4).
& Определение. Полустепенью исхода (захода) вершины v орграфа D называется число deg–(v) (deg+(v)) дуг орграфа D, исходящих из v (заходящих в v).
В случае ориентированного псевдографа вклад каждой петли, инцидентной вершине v, равен 1 как в deg–(v), так и в deg+(v).
& Определение. Регулярный граф – граф, степень каждой вершины которого равна r.
? Замечание. Графы Kn являются регулярными графами степени
n – 1.
& Определение. Граф G называется двудольным, если его множество вершин графа можно разбить на два непересекающихся подмножества: 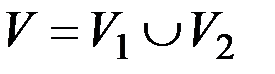 , причем для любого ребра x = {vi, vj} вершины vi и vj принадлежат разным подмножествам.
, причем для любого ребра x = {vi, vj} вершины vi и vj принадлежат разным подмножествам.
|
|
|
Если каждая вершина из 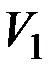 соединена ребром с каждой из
соединена ребром с каждой из  , то граф называется полным двудольным графом, обозначается
, то граф называется полным двудольным графом, обозначается  , где q, n – мощности подмножеств
, где q, n – мощности подмножеств 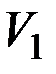 и
и 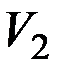 , т. е.
, т. е. 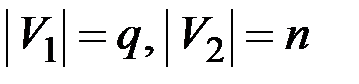 .
.
Пример
v На рис. 2.6 показан граф 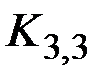 .
.

Рис. 2.6. Полный двудольный граф K3,3
& Лемма о рукопожатиях. Если в графе 
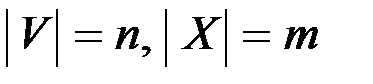 , то
, то 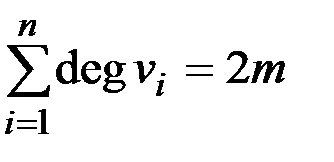 .
.
Доказательство леммы очевидно: каждое ребро в этой сумме участвует ровно 2 раза, так как имеет 2 конца.
& Следствие. Число вершин графа G с нечетной степенью четно.
& Определение. Графы 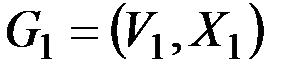 и
и 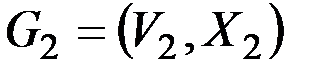 называются изоморфными, если существует биекция
называются изоморфными, если существует биекция  , причем, если пара
, причем, если пара  , то пара
, то пара  и наоборот.
и наоборот.
Таким образом, одна и та же система объектов и связей между ними может быть изображена разными способами. Способы эти и будут изоморфными графами. Для установления изоморфизма достаточно одинаково занумеровать вершины графа множества 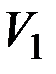 и соответствующие им при биекции f вершины множества
и соответствующие им при биекции f вершины множества 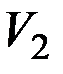 .
.
Пример
v На рис. 2.7 показаны примеры изоморфных графов
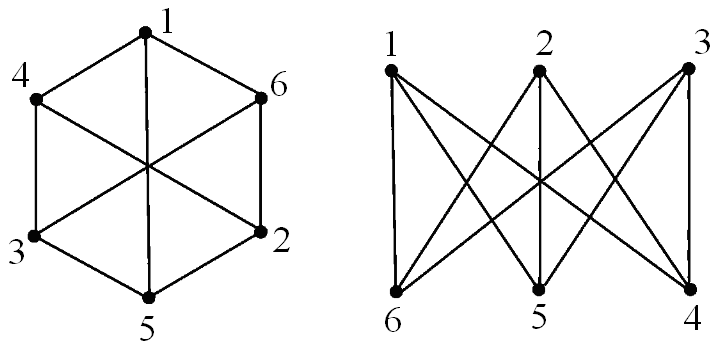
а б
Рис. 2.7. Пары изоморфных графов
Отношение изоморфизма графов представляет собой отношение эквивалентности и позволяет произвести разбиение исходного класса всех графов на классы эквивалентности (см. подглаву 1.4).
& Определение. Дополнительный граф (или дополнение) графа  – это граф
– это граф  , определяемый следующим образом:
, определяемый следующим образом:  , и любые две несовпадающие вершины смежны в
, и любые две несовпадающие вершины смежны в 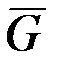 тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в  (рис. 2.8, а, б).
(рис. 2.8, а, б).
а б в
Рис. 2.8. Граф (a), его дополнение (б), самодополнительный граф (в)
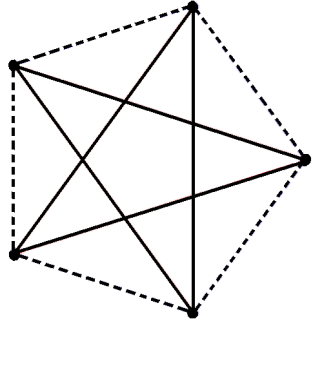
Очевидно, что 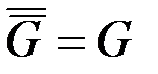 и объединение
и объединение 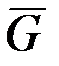 и
и 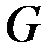 дает полный граф на том же множестве вершин. Граф изоморфный своему дополнению, называется самодополнительным.
дает полный граф на том же множестве вершин. Граф изоморфный своему дополнению, называется самодополнительным.
Пример
v На рис.2.8,в показан пунктиром граф, который изоморфен своему дополнению, графу, изображенному сплошной линией.
2.2. Маршруты и пути
& Определение. Последовательность v1x1v2x2v3…xkvk+1, (где 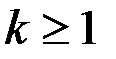 , viÎV, i = 1,…,k + 1, xjÎX, j=1,…,k), в которой чередуются вершины и ребра (дуги) и для каждого j=1,…,k ребро (дуга) xj имеет вид {vj,vj+1} (для орграфа (vj,vj+1)), называется маршрутом, соединяющим вершины v1 и vk+1 (путем из v1 в vk+1).
, viÎV, i = 1,…,k + 1, xjÎX, j=1,…,k), в которой чередуются вершины и ребра (дуги) и для каждого j=1,…,k ребро (дуга) xj имеет вид {vj,vj+1} (для орграфа (vj,vj+1)), называется маршрутом, соединяющим вершины v1 и vk+1 (путем из v1 в vk+1).
Маршрут (путь) называется замкнутым, если начальная вершина совпадает с конечной v1=vk+1.
Пример
v В графе на рис.2.4 v1x1v2x2v3x4v4x3v2 – маршрут, v2x2v3x4v4 – подмаршрут; маршрут можно восстановить и по записи x1x2x4x3; если кратности ребер (дуг) равны 1, можно записать и так: v1v2v3v4v2.
& Определения
Цепь − незамкнутый маршрут (путь), в котором все ребра (дуги) различны, т.е. не повторяются.
Цикл (контур) − замкнутый маршрут (путь), в котором все ребра (дуги) различны, т.е. не повторяются.
Простая цепь – цепь, в которой все вершины различны.
Простой цикл (контур) − цикл (контур), в котором все вершины (кроме первой и последней) различны, т.е. не повторяются.
Гамильтонова цепь (цикл, контур) – простая цепь (цикл, контур), проходящая через все вершины.
Эйлерова цепь (цикл, контур) – цепь (цикл, контур), содержащая все ребра (дуги) графа по одному разу.
Длина маршрута (пути) – число ребер в маршруте (дуг в пути).
Пример
v Рассмотрим 4 графа и определим наличие в них эйлеровых и гамильтоновых цепей и циклов.
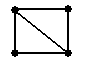
| Граф | Эйлеров цикл | Эйлерова цепь | Гамильнонов цикл | Гамильтонова цепь |
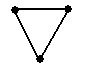
| ü | û | ü | ü |
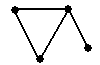
| û | ü | ü | ü |
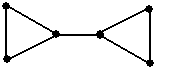
| û | ü | û | ü |
| û | ü | û | ü |
& Утверждение 1
Для того чтобы связный (для любых двух вершин графа существует маршрут их соединяющий, см. подглаву 2.4) псевдограф G обладал эйлеровым циклом, необходимо и достаточно, чтобы степени всех его вершин были четными.
& Утверждение 2
Для того чтобы связный псевдограф G обладал эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.
В псевдографе G (в ориентированном псевдографе D) из всякого цикла (контура) можно выделить простой цикл (простой контур).
Из всякого незамкнутого маршрута (пути) можно выделить простую цепь с теми же начальной и конечной вершинами.
& Определение. Минимальный маршрут (путь) – маршрут (путь) с наименьшим числом ребер (дуг).
Каждый минимальный маршрут (путь) является простой цепью. Пусть  – минимальный маршрут (путь) в графе G (в орграфе D). Тогда для любых i и j таких, что
– минимальный маршрут (путь) в графе G (в орграфе D). Тогда для любых i и j таких, что  , маршрут (подпуть)
, маршрут (подпуть) 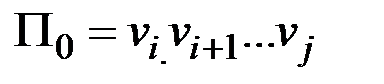 тоже является минимальным.
тоже является минимальным.
Эйлеровы и гамильтоновы циклы сходны по способу задания. Но, несмотря на внешнее сходство, задачи их поиска резко отличаются по степени трудности. Для решения вопроса о наличии эйлерова цикла или цепи в графе достаточно применить утверждения 1 и 2. Критерий же существования гамильтонова цикла в произвольном графе еще не найден.
Решение этой проблемы имеет практическую ценность, так как к ней близка известная задача о коммивояжере (см. подглаву 2.7), который должен объехать несколько пунктов и вернуться обратно. Он обязан побывать в каждом пункте в точности по одному разу и заинтересован в том, чтобы затратить на поездку как можно меньше времени. А для этого требуется определить все варианты посещения городов и подсчитать в каждом случае затрату времени.
Рассмотрим несколько достаточных условий существования гамильтоновых циклов в графе.
1) Всякий полный граф содержит гамильтонов цикл.
Действительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа.
2) Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он все равно содержит гамильтонов цикл.
Если граф, содержащий гамильтонов цикл, объединить с еще одной вершиной ребром так, что образуется висячая вершина, то такой граф больше не содержитгамильтонов цикл.
Поиск необходимого и достаточного условия для того, чтобы граф содержал гамильтонов цикл, стал одной из главных задач теории графов. О таких графах известно немного. Большинство известных теорем имеет вид «если граф G имеет достаточное число ребер, то он содержит гамильтонов цикл». Вероятно, самой знаменитой из этих теорем является теорема, принадлежащая Г.Э. Дираку.
& Теорема Дирака. Если в связном простом графе 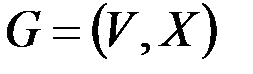
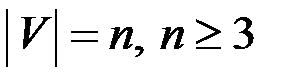 , степени всех его вершин
, степени всех его вершин  (
( 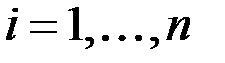 ), то граф содержит гамильтонов цикл. Обратное не верно.
), то граф содержит гамильтонов цикл. Обратное не верно.
2.3. Матрицы смежности и инцидентности
Пусть D=(V, X) орграф, V = {v1,...,vn}, X = {x1,...,xm}.
& Определение . Матрица смежности орграфа D − квадратная матрица A(D) = [aij] порядка n, где

& Определение. Матрица инцидентности − матрица B(D) = [bij] порядка n´m, где

& Определение. Матрицей смежности неориентированного графа G = (V, X) называется квадратная симметричная матрица A(G) = [aij] порядка n, где
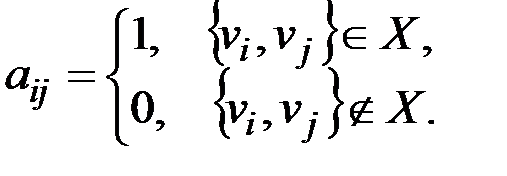
& Определение. Матрицей инцидентности графа G называется матрица B(G) = [bij] порядка n´m, где
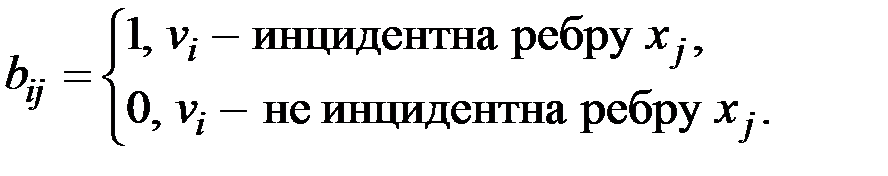
Пример
v Для орграфа на рис. 2.9 матрицы смежности и инцидентности имеют вид:
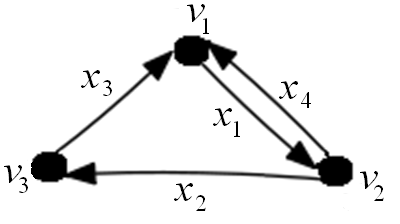
Рис. 2.9. Пример орграфа для построения матриц A(D) и B(D)
матрица смежности матрица инцидентности
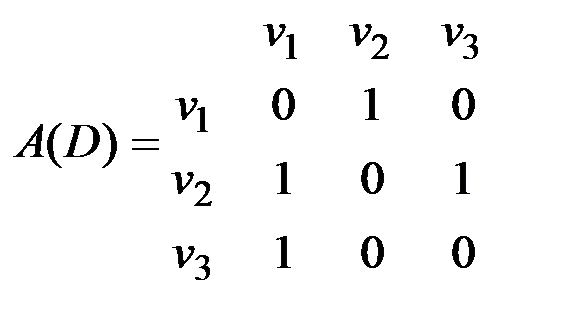
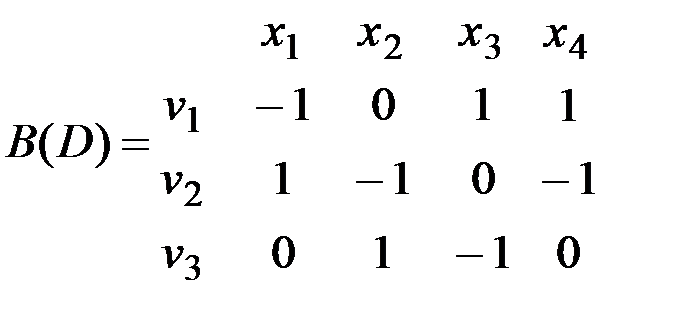 .
.
? Замечание. Для изоморфных графов, вершины которых занумерованы произвольным образом, матрицы смежности различны, но они получаются друг из друга одинаковыми перестановками строк и столбцов. То же самое верно для матриц инцидентности.
& Определение. Матрицей Кирхгофа называют квадратную матрицу K(G)=[kij] порядка  , где
, где

Сумма элементов в каждой строке и в каждом столбце матрицы равна 0.
Пример
v Матрица Кирхгофа для графа на рис. 2.10
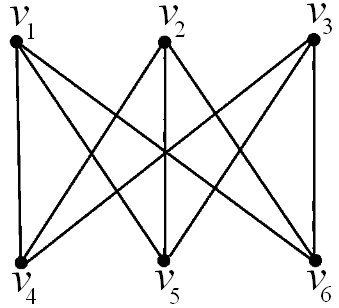
Рис. 2.10. Пример графа для получения матрицы Кирхгофа

 .
.
2.4. Связность. Компоненты связности
& Определение. Подграфом графа G (орграфа D) называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G (D).
Подграф называется собственным, если он отличен от самого графа.
? Замечание. Говорят, что вершина w графа G (орграфа D) достижима из вершины v, если либо w=v, либо существует маршрут (путь) из v в w.
& Определение. Неориентированный граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v и w.
Орграф называется односторонне связным, если для любых двух его вершин, по крайней мере, одна достижима из другой.
Орграф называется слабо связным, если соответствующий неориентированный граф является связным.
Связность вершин неориентированного графа, как и сильная связанность вершин орграфа задает некоторое отношение 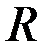 на множестве вершин. Рассмотрим R для орграфа. Пара
на множестве вершин. Рассмотрим R для орграфа. Пара 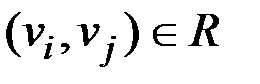 тогда и только тогда, когда существует путь из вершины
тогда и только тогда, когда существует путь из вершины  в
в 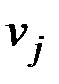 . Будем считать, что
. Будем считать, что  (длина пути в этом случае равна 0). Если
(длина пути в этом случае равна 0). Если  , то
, то 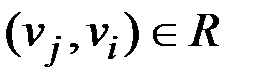 . Если
. Если 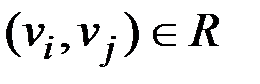 и
и 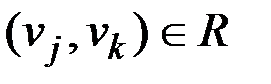 , тогда, очевидно
, тогда, очевидно 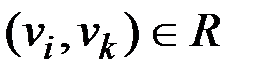 , таким образом, отношение
, таким образом, отношение  рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности (см. подглаву 1.4).Отношение эквивалентности позволяет разбить множество вершин
рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности (см. подглаву 1.4).Отношение эквивалентности позволяет разбить множество вершин 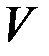 на классы эквивалентности:
на классы эквивалентности:
 ,
,
где 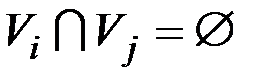 .
.
Две вершины 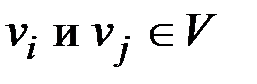 связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
связаны тогда и только тогда, когда они принадлежат одному классу эквивалентности.
& Определение. Компонентой связности графа G (сильной связности орграфа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (орграфа D).
Каждый неориентированный граф единственным образом представляется в виде объединения своих компонент связности.
Примеры
v На рис. 2.11 показан граф, состоящий из четырех компонент связности.
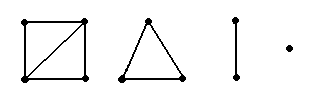
Рис. 2.11. Пример неориентированного графа из четырех компонент связности
v Примеры компонент сильной связности орграфов приведены на рис. 2.12, причем компонентой сильной связности может быть и изолированная вершина, так на рис. 2.12, в показаны две компоненты сильной связности.

а б в
Рис. 2.12. Примеры компонент сильной связности орграфов
& Теорема о связи вершин с нечетными степенями
Если в графе  есть ровно 2 вершины с нечетными степенями, то они связаны.
есть ровно 2 вершины с нечетными степенями, то они связаны.
Доказательство.Пусть  и
и 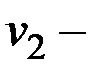 вершины с нечетными степенями. Если они принадлежат одной компоненте связности, то они связаны. Если они принадлежат разным компонентам связности, т. е.
вершины с нечетными степенями. Если они принадлежат одной компоненте связности, то они связаны. Если они принадлежат разным компонентам связности, т. е. 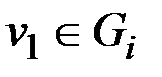 ,
, 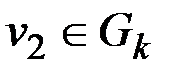 , то в графе
, то в графе 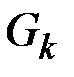 , например, всего одна вершина с нечетной степенью, чего не может быть.
, например, всего одна вершина с нечетной степенью, чего не может быть.
& Лемма о присоединении ребра
Если 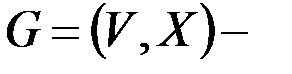 связный граф,
связный граф, 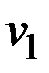 и
и 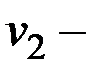 две разные его вершины и
две разные его вершины и 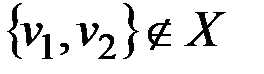 , тогда добавление к графу ребра
, тогда добавление к графу ребра 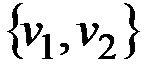 приводит к образованию простого цикла.
приводит к образованию простого цикла.
Доказательство. 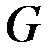 – связный граф, поэтому существует маршрут
– связный граф, поэтому существует маршрут 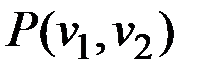 , в нем можно выделить подмаршрут
, в нем можно выделить подмаршрут 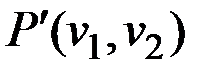 , который будет простой цепью.
, который будет простой цепью.
Маршрут  , который получается из
, который получается из 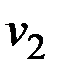 в
в  по вершинам и ребрам пути
по вершинам и ребрам пути  , также будет простой цепью. Рассмотрим маршрут:
, также будет простой цепью. Рассмотрим маршрут: 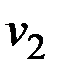 ,
,  ,
, 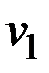 ,
, 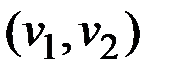 ,
, 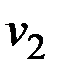 , он будет простым циклом.
, он будет простым циклом.
& Лемма об удалении ребра
Пусть 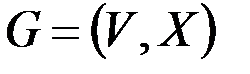 – связный граф, ребро
– связный граф, ребро  входит в цикл
входит в цикл 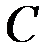 , тогда граф
, тогда граф 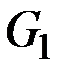 , полученный из
, полученный из 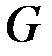 удалением ребра
удалением ребра 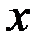 , будет связным.
, будет связным.
Доказательство. Пусть 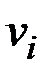 и
и 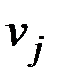 – произвольные вершины графа. Так как граф
– произвольные вершины графа. Так как граф  связный, то существует маршрут
связный, то существует маршрут 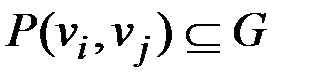 . Если этот маршрут не содержит ребро
. Если этот маршрут не содержит ребро 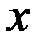 , то
, то  , т. е. эти вершины связаны маршрутом и в графе
, т. е. эти вершины связаны маршрутом и в графе 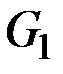 . Если
. Если 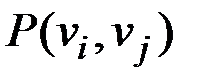 проходит по ребру x, тогда он имеет вид
проходит по ребру x, тогда он имеет вид 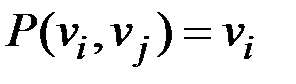 ,
, 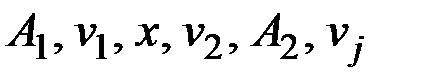 , где
, где  – последовательности ребер и вершин. Ребро
– последовательности ребер и вершин. Ребро 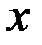 входит в цикл
входит в цикл 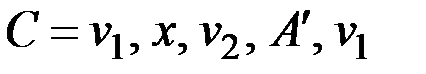 , следовательно, существует цепь
, следовательно, существует цепь  , тогда существует
, тогда существует 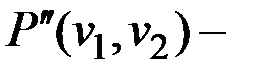 противоположная цепь. Рассмотрим в этом случае маршрут
противоположная цепь. Рассмотрим в этом случае маршрут  , который не содержит ребро
, который не содержит ребро 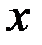 и связывает вершины
и связывает вершины  и в
и в  в графе
в графе 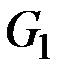 , следовательно,
, следовательно, 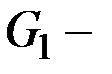 связный граф.
связный граф.
& Лемма о числе компонент связности
Пусть G=(V,X) – простой граф, 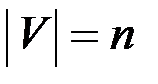 ,
, 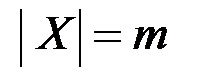 , k – количество компонент связности, тогда
, k – количество компонент связности, тогда
 .
.
Причем, если в G нет циклов, то
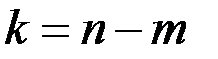 .
.
& Лемма о максимальном числе ребер в графе
Пусть G = (V, X) – простой граф, 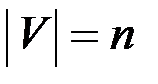 , k – количество компонент связности, тогда максимальное число ребер в графе будет
, k – количество компонент связности, тогда максимальное число ребер в графе будет
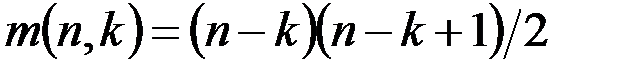 .
.
& Следствие. Если  , то
, то  и это максимальное число ребер при двух компонентах связности, поэтому если
и это максимальное число ребер при двух компонентах связности, поэтому если
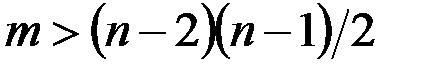 ,
,
то граф связный.
? Замечание. Для связного графа 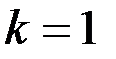 и
и 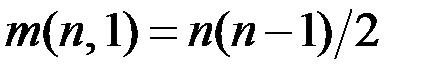 , а это число ребер в полном графе.
, а это число ребер в полном графе.
Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где 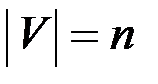 . Обозначим через
. Обозначим через 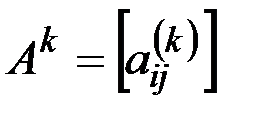 k-ю степень матрицы смежности A(D) (или A(G)).
k-ю степень матрицы смежности A(D) (или A(G)).
Элемент 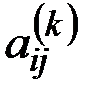 матрицы Ak ориентированного псевдографа D=(V,X) (псевдографа G = (V,X)) равен числу всех путей (маршрутов) длины k из vi в vj.
матрицы Ak ориентированного псевдографа D=(V,X) (псевдографа G = (V,X)) равен числу всех путей (маршрутов) длины k из vi в vj.
& Определение. Матрица достижимости орграфа D − квадратная матрица T(D) = [tij] порядка n, элементы которой равны
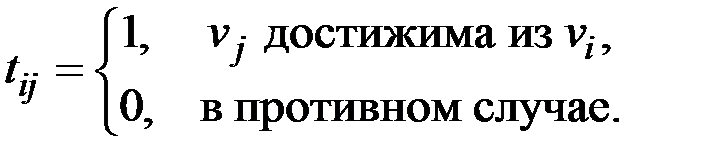 .
.
& Определение. Матрица сильной связности орграфа D – квадратная матрица S(D) = [sij] порядка n, элементы которой равны
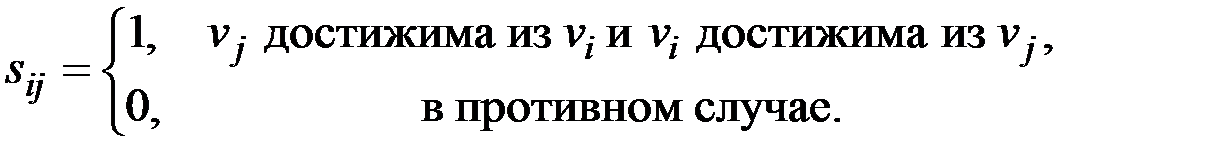
& Определение. Матрица связности графа G − квадратная матрица S(G) = [sij] порядка n, элементы которой равны
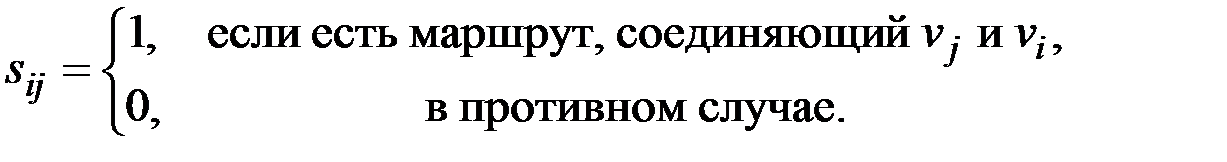
Для того чтобы n-вершинный орграф D с матрицей смежности A(D) имел хотя бы один контур, необходимо, чтобы матрица K = A2 + A3 +…+ An имела хотя бы один ненулевой диагональный элемент.
Если A(D) – матрица смежности графа D, то элемент 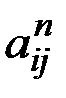 матрицы Ап равен числу путей длины п, соединяющих вершины vi и vj графа D.
матрицы Ап равен числу путей длины п, соединяющих вершины vi и vj графа D.
В некоторых случаях при вычислениях степеней матрицы A(D) важно знать не число соответствующих путей, а только есть ли в графе эти пути или нет. Тогда при вычислении элементов матриц A2, A3,…, An–1 используют функцию sign, которая равна 1, если число положительное, и 0, если число равно 0. В результате матрицы sign[A2], sign[A3], ..., sign[An–1] состоят только из нулей и единиц.
& Утверждение 3
Пусть D=(V, X) – орграф, 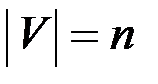 , A(D) – его матрица смежности. Тогда матрица достижимости находится следующим образом:
, A(D) – его матрица смежности. Тогда матрица достижимости находится следующим образом:
T(D) = sign[E+A+A2+A3+…+An–1],
где E – единичная матрица порядка n.
Матрица сильной связности орграфа находится по формуле
S(D) = T(D)&TT(D),
где TT – транспонированная матрица достижимости, операция «&» обозначает поэлементное умножение матриц, т. е. каждый элемент матрицы S(D) равен  произведению соответствующих элементов из матриц T(D) и TT(D).
произведению соответствующих элементов из матриц T(D) и TT(D).
Пусть G = (V, X) – неориентированный граф, 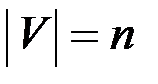 , A(G) – его матрица смежности. Тогда его матрица связности находится аналогично матрице достижимости орграфа
, A(G) – его матрица смежности. Тогда его матрица связности находится аналогично матрице достижимости орграфа
S(G) = sign[E + A + A2 + A3 +…+ An–1].
Под операцией удаления вершины из графа (орграфа) будем понимать операцию, заключающуюся в удалении некоторой вершины вместе с инцидентными ей ребрами (дугами).
& Определение. Вершина графа, удаление которой увеличивает число компонент связности, называется точкой сочленения.
Пример
v На рис. 2.13 точками сочленения графа являются вершины v3, v4, v6, v7.
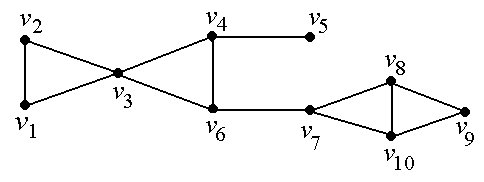
Рис. 2.13. Пример графа с точками сочленения
2.5. Расстояния, нагруженный граф, деревья
Пусть 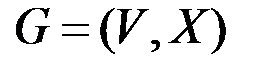 – неориентированный граф (или псевдограф).
– неориентированный граф (или псевдограф).
& Определение. Расстоянием между вершинами  называется минимальная длина маршрута между ними, при этом
называется минимальная длина маршрута между ними, при этом 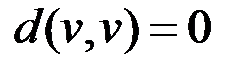 ,
,  , если не существует маршрута.
, если не существует маршрута.
Условно понятие расстояния применимо и для орграфа.
Расстояние в графе удовлетворяет аксиомам метрики:
ü 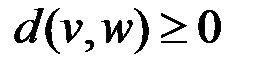 ,
, 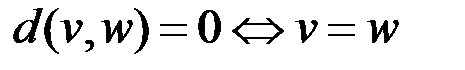 ;
;
ü  (в неориентированном графе);
(в неориентированном графе);
ü  ;
;
ü 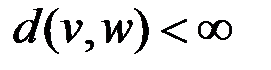 в связном неориентированном графе.
в связном неориентированном графе.
Пусть 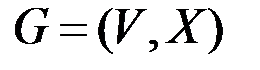 связный граф (или псевдограф).
связный граф (или псевдограф).
& Определения
Диаметром графа G называется величина
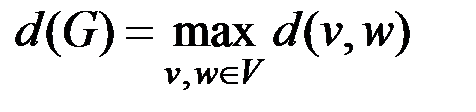 .
.
Пусть 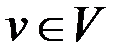 .
.
Максимальным удалением (эксцентриситетом) в графе G от вершины 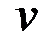 называется величина
называется величина
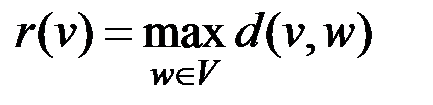 .
.
Радиусом графа G называется величина
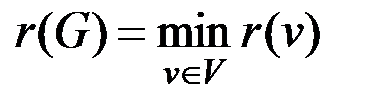 .
.
Центром графа G называется любая вершина 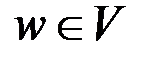 такая, что
такая, что  .
.
? Замечание. Приведенные метрические характеристики (диаметр, эксцентриситет, центр, радиус) определяются и в орграфе.
Пусть 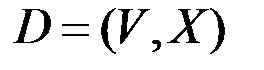 орграф,
орграф, 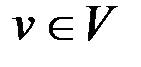 – некоторая вершина,
– некоторая вершина,  .
.
Обозначим  – образ вершины v;
– образ вершины v;
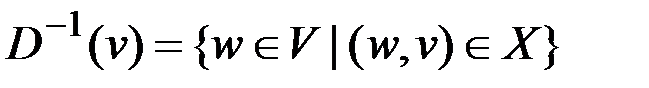 – прообраз вершины v;
– прообраз вершины v;
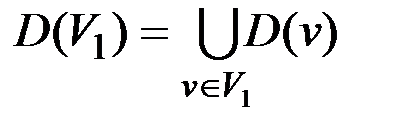 – образ множества вершин V1;
– образ множества вершин V1;
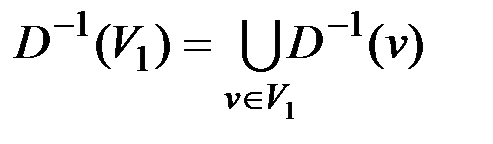 – прообраз множества вершин V1.
– прообраз множества вершин V1.
? Замечание. В графе G образ и прообраз вершины совпадают.
& Определение. Нагруженный граф – граф G = (V, X) (D = (V, X)), на множестве ребер (дуг) которого определена некоторая функция  R, которую называют весовой функцией.
R, которую называют весовой функцией.
Пример
v Пусть D = (V, X) – нагруженный орграф (рис.2.14). Цифра над дугой обозначает вес дуги.

Рис. 2.14. Пример нагруженного графа
Для любого пути П нагруженного орграфа D через l(П) обозначаем сумму длин дуг, входящих в путь П. (Каждая дуга считается столько раз, сколько раз она входит в путь П).
Введем матрицу длин дуг C(D) = [cij] порядка n, причем
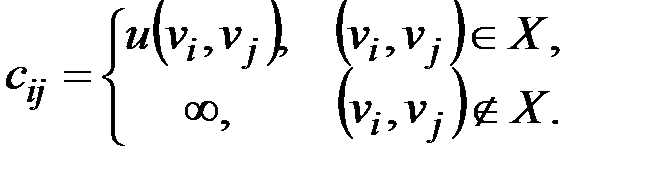
Величина u называется длиной пути. Если выбрать веса равными 1, то придем к ненагруженному графу.
& Определение. Путь в нагруженном орграфе из вершины v в вершину w, где v ¹ w, называется минимальным, если он имеет наименьшую длину.
? Замечание. Аналогично определяется минимальный маршрут в нагруженном неориентированном графе.
Заметим, что иногда веса дуг (ребер) могут быть отрицательными. При этом важно, есть ли циклы отрицательного веса. Если из вершины vi можно добраться до цикла отрицательного веса, то потом можно обходить этот цикл сколь угодно долго, и вес будет все уменьшаться, так что для вершин этого цикла кратчайших путей не существует.
Свойства минимальных путей (маршрутов) в нагруженном графе
1. Если для любой дуги (ребра) 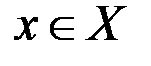 ,
,  , то любой минимальный путь (маршрут) является простой цепью.
, то любой минимальный путь (маршрут) является простой цепью.
2. Если 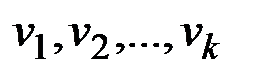 минимальный путь (маршрут) то для любых i, j:
минимальный путь (маршрут) то для любых i, j:  путь (маршрут)
путь (маршрут)  тоже является минимальным.
тоже является минимальным.
3. Если 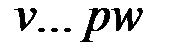 – минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k + 1 дуг (ребер), то
– минимальный путь (маршрут) среди путей (маршрутов) из v в w, содержащих не более k + 1 дуг (ребер), то  – минимальный путь (маршрут) из v в p среди путей (маршрутов), содержащих не более k дуг (ребер).
– минимальный путь (маршрут) из v в p среди путей (маршрутов), содержащих не более k дуг (ребер).
Деревья
& Определение. Граф G называется деревом, если он является связным и не имеет циклов.
& Определение. Граф G называется лесом, если все его компоненты связности – деревья.
Следующие утверждения эквивалентны:
1. Граф G есть дерево.
2. Граф G является связным и число его ребер ровно на 1 меньше числа вершин.
3. " две различные вершины графа G можно соединить единственной (и при этом простой) цепью.
4. Граф G не содержит циклов, но, добавляя к нему любое новое ребро, получаем ровно один и притом простой цикл.
& Утверждение 4
Если у дерева G имеется, по крайней мере, одно ребро, то у него найдется висячая вершина.
& Утверждение 5
Пусть G связный граф, а 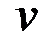 – висячая вершина в G, граф
– висячая вершина в G, граф  получается из G в результате удаления вершины v и инцидентного ей ребра. Тогда
получается из G в результате удаления вершины v и инцидентного ей ребра. Тогда 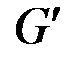 тоже является связным.
тоже является связным.
& Определение. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пусть G – связный граф. Тогда остовное дерево графа G должно содержать n(G) – 1 ребер. Значит, для получения остовного дерева из графа G нужно удалить 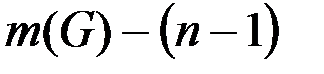 ребер.
ребер.
& Определение . Число  называется цикломатическим числом графа G.
называется цикломатическим числом графа G.
& Теорема Кирхгофа. Число остовных деревьев в связном графе  порядка
порядка 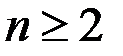 равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
равно алгебраическому дополнению любого элемента матрицы Кирхгофа.
Пример
v Рассмотрим граф 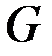 на рис. 2.15.
на рис. 2.15.

Рис. 2.15. Пример графа для нахождения количества остовных деревьев
Матрица Кирхгофа для этого графа имеет вид
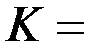
 .
.
Найдем алгебраическое дополнение элемента 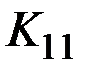 .
.
 .
.
Действительно, у графа  3 остовных дерева:
3 остовных дерева:

Рис. 2.16. Остовные деревья графа, показанного на рис. 2.15
& Определения
Ориентированным деревомназывается орграф без циклов, во все вершины которого, кроме одной, входит ровно одна дуга.
Единственная вершина, из которой дуги только выходят, называется корнем дерева.
Остальные вершины называются узлами дерева.
Вершины с нулевой полустепенью исхода (из которых не исходит ни одна дуга) называются листьями.
Путь из корня в лист называется ветвью дерева.
Пример
v На рис. 2.17 приведены примеры ориентированных деревьев.
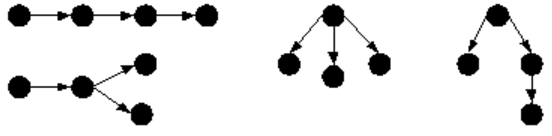
Рис. 2.17. Ориентированные деревья
Из определения дерева следует, что корень связан единственным путем с любой другой вершиной дерева.
Частный случай ориентированных деревьев – корневые деревья, при этом корневые деревья бывают и неориентированные. Данный вид деревьев используется в процедурах поиска в информационных системах, при переборе вариантов в компьютерных программах и др.
Рассмотрим корневое изображение – «геометрическое» представление корневого дерева.
Множество вершин произвольного дерева G можно разбить в объединение непустых попарно непересекающихся подмножеств V0,V1,...,Vk так, что будут выполнены следующие условия:
1) множество V0 состоит из одной вершины;
2) для всякого i=1,...,k никакие вершины из Vi не смежны;
3) для всякого i=1,...,k любая вершина из Vi смежна ровно с одной вершиной из Vi−1 и не смежна ни с одной вершиной из Vi−2,...,V0.
На рис. 2.18 приведены дерево и одно из его корневых изображений (одно и то же дерево имеет много корневых изображений, в зависимости от выбора корня).
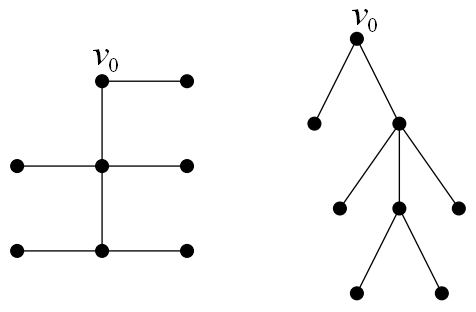
Рис. 2.18. Дерево и одно из его корневых изображений
& Определение. Упорядоченным корневым деревом называется корневое дерево  , в котором задан порядок его поддеревьев и каждое поддерево – упорядоченное дерево.
, в котором задан порядок его поддеревьев и каждое поддерево – упорядоченное дерево.
Упорядоченное корневое дерево получается помещением корневого дерева в полуплоскость и заданием порядка (например, слева направо) ребер, инцидентных каждому узлу.
Получим оценку числа упорядоченных корневых деревьев. Для этого введем кодировку упорядоченных корневых деревьев. Дереву  поставим в соответствие пустое слово. Пусть упорядоченное корневое дерево имеет поддеревья
поставим в соответствие пустое слово. Пусть упорядоченное корневое дерево имеет поддеревья  и каждому поддереву
и каждому поддереву  поставлен в соответствие код
поставлен в соответствие код 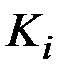 . Тогда кодом дерева
. Тогда кодом дерева 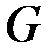 будет код
будет код 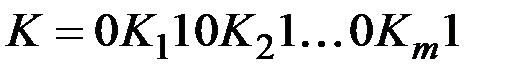 .
.
Так как корневыми деревьями являются только деревья, которые могут быть построены в соответствии с определением, то все они могут быть закодированы.
Из определения кода дерева следует, что код дерева – это слово из нулей и единиц.
& Лемма о коде дерева
Пусть 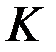 – код упорядоченного корневого дерева
– код упорядоченного корневого дерева 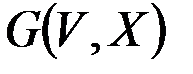 . Обозначим через
. Обозначим через  – число нулей,
– число нулей, 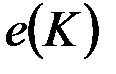 – число единиц в коде,
– число единиц в коде, 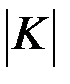 – общее число символов. Пусть
– общее число символов. Пусть  , где
, где 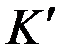 и
и  два подслова. Тогда
два подслова. Тогда
а) 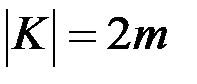 , где
, где 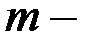 число ребер в дереве
число ребер в дереве  ;
;
б)  ;
;
в) 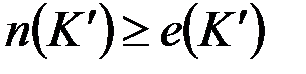 , причем равенство достигается только тогда, когда
, причем равенство достигается только тогда, когда  , где
, где  – коды первых
– коды первых 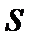 поддеревьев дерева
поддеревьев дерева  .
.
В коде дерева можно выделить коды отдельных поддеревьев. Для этого надо найти точки, где количество нулей совпадает с количеством единиц, т. е. надо найти  и т. д. Затем в каждом
и т. д. Затем в каждом 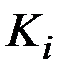 проделать такую же процедуру. Таким образом, по коду упорядоченного корневого дерева можно восстановить само дерево.
проделать такую же процедуру. Таким образом, по коду упорядоченного корневого дерева можно восстановить само дерево.
& Теорема о числе упорядоченных корневых деревьев
Число упорядоченных корневых деревьев с 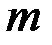 ребрами не превосходит
ребрами не превосходит  .
.
Доказательство. Так как между упорядоченными корневыми деревьями и их кодами существует биекция, то их число равно числу кодов деревьев. Код дерева с 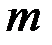 ребрами – слово длины
ребрами – слово длины 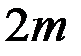 , состоящее из нулей и единиц.
, состоящее из нулей и единиц.
Число кодов не превосходит общего числа слов длины  , состоящих из
, состоящих из  и
и  , которое равно
, которое равно 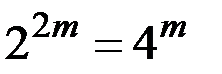 . Таким образом, число упорядоченных корневых деревьев с
. Таким образом, число упорядоченных корневых деревьев с 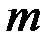 ребрами не превосходит
ребрами не превосходит  .
.
& Следствия
1. Число попарно неизоморфных неупорядоченных корневых деревьев с  ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит
ребрами не превосходит числа упорядоченных корневых деревьев и, следовательно, не превосходит  .
.
2. Число попарно неизоморфных деревьев с  ребрами не превосходит числа корневых деревьев с
ребрами не превосходит числа корневых деревьев с  ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит
ребрами, так как они различаются выбором корневой вершины, следовательно, не превосходит 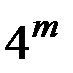 .
.
Пример
v Деревья, приведенные на рис. 2.19, попарно изоморфны, но различны с точки зрения корневых деревьев.
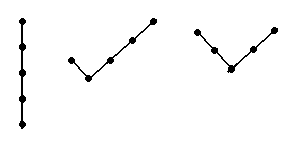
Рис. 2.19. Изоморфные деревья
Задача о соединении городов. Пусть есть 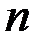 городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
городов, расстояние между каждыми двумя городами известно. Надо соединить их дорогой минимальной длины (или минимальной стоимости, если известна цена дороги между каждыми двумя городами).
Эту задачу можно сформулировать на языке теории графов, полагая города вершинами, а расстояния – ребрами нагруженного графа. Пусть каждому ребру графа поставлено в соответствие положительное число 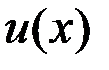 (расстояние между городами или стоимость прокладываемой дороги). Обозначим вес всего графа
(расстояние между городами или стоимость прокладываемой дороги). Обозначим вес всего графа
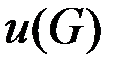 , тогда
, тогда
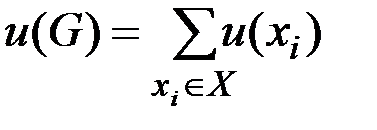 .
.
Стоит следующая задача: дан простой полный граф на  вершинах, задан вес каждого ребра, надо построить связный подграф минимального веса. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимального веса.
вершинах, задан вес каждого ребра, надо построить связный подграф минимального веса. (Требование полноты исходного графа необязательно, достаточно, чтобы он был связным). Очевидно, что минимальный связный граф – дерево, поэтому задачу можно уточнить: построить остовное дерево минимального веса.
Алгоритм Краскала
Данный алгоритм используется дляпостроения остовного дерева минимального веса.
Выберем ребро минимального веса, обозначим его 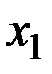 . Если несколько ребер имеют один и тот же вес, берем любое. Затем выбираем ребро минимального веса из оставшихся, обозначим его
. Если несколько ребер имеют один и тот же вес, берем любое. Затем выбираем ребро минимального веса из оставшихся, обозначим его
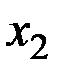 . Затем снова выбираем ребро минимального веса из оставшихся, но так чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом
. Затем снова выбираем ребро минимального веса из оставшихся, но так чтобы оно не образовывало цикла с выбранными ранее ребрами. Выбрав таким образом  ребро, получим остовное дерево
ребро, получим остовное дерево 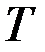 , причем
, причем
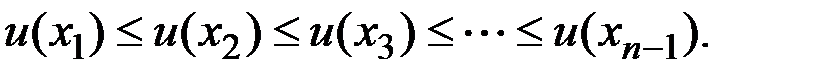
Покажем, что не будет остовных деревьев с весом меньшим, чем вес дерева 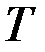 .
.
Пусть есть остовное дерево 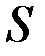 такое, что
такое, что 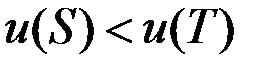 . Пусть
. Пусть 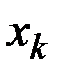 – первое ребро из
– первое ребро из 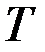 , не вошедшее в
, не вошедшее в 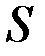 . Рассмотрим граф
. Рассмотрим граф  , он не является деревом, следовательно, в нем существует цикл
, он не является деревом, следовательно, в нем существует цикл 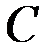 . Пусть
. Пусть 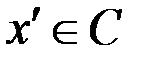 и
и 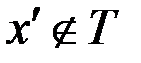 , такое ребро существует, так как
, такое ребро существует, так как 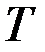 – дерево и не содержит циклов, удалив это ребро из графа
– дерево и не содержит циклов, удалив это ребро из графа 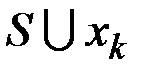 , получим граф
, получим граф 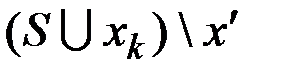 , он связный граф, в нем
, он связный граф, в нем  ребро, следовательно, он дерево. При этом графы
ребро, следовательно, он дерево. При этом графы 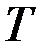 и
и 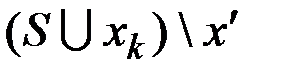 содержат на одно общее ребро больше, чем графы
содержат на одно общее ребро больше, чем графы  и
и 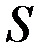 .
.

так как 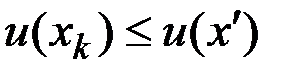 , иначе при построении дерева
, иначе при построении дерева 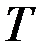 по алгоритму Краскала вместо ребра
по алгоритму Краскала вместо ребра  взяли бы ребро
взяли бы ребро 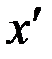 (ребра
(ребра  ) у деревьев
) у деревьев  и
и 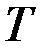 общие и
общие и 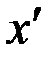 не образует с ними цикла).
не образует с ними цикла).
Пусть 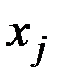 следующее ребро из
следующее ребро из 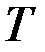 , не вошедшее в
, не вошедшее в 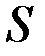 . Присоединим его к графу
. Присоединим его к графу 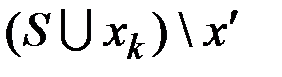 , вновь образуется цикл, удалим из него ребро
, вновь образуется цикл, удалим из него ребро 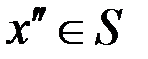 и
и  . Получим граф
. Получим граф  этот граф и граф
этот граф и граф 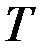 будут иметь на 2 общих ребра больше, чем графы
будут иметь на 2 общих ребра больше, чем графы  и
и 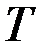 , при этом
, при этом
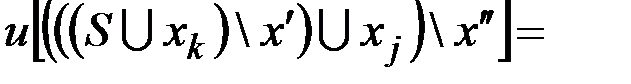
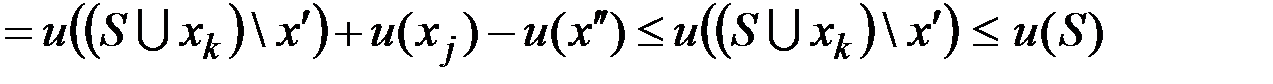 .
.
Повторив эту процедуру конечное число раз, перестроим граф  в
в 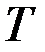 и получим противоречие
и получим противоречие
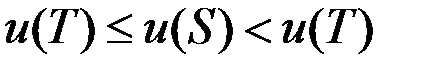 .
.
Подробнее сам алгоритм и пример его использования приведены в подглаве 2.7.10.
Дерево порядка n называется помеченным, если его вершинам присвоены некоторые метки, например 1, 2, ..., n.
Как ранее было сказано, каждому дереву можно поставить в соответствие некоторый код. С помощью этого кода можно восстановить дерево с точностью до изоморфизма.
Существуют различные способы кодирования деревьев, которые позволяют решать конкретные задачи (подсчет деревьев, установление изоморфизма, генерирование всех неизоморфных деревьев и т. д.).
Таким образом, кодирование графасостоит в записи информации о нем, однозначно и полностью восстанавливающей структуру графа.
Рассмотрим так называемый код Прюфера, который представляет из себя способ однозначного кодирования помеченного дерева с помощью последовательности чисел.
С помощью кода Прюфера в том числе демонстрируется решение задачи о количестве способов добавить в заданный граф ребра, чтобы превратить его в связный.
Код Прюфера
Упаковка дерева. Помеченные деревья порядка n переводятся в последовательность чисел по алгоритму:
1. Выбирается лист с минимальным номером.
2. Лист и инцидентное ребро удаляются из дерева, в последовательность Прюфера добавляется номер смежной удаленной вершины.
3. Если в дереве больше двух вершин, то п. 1, иначе – выход.
Распаковка дерева. Отметим, что код содержит элементов на 2 меньше количества вершин восстанавливаемого графа.
Обозначим P = (p1, p2, ..., p n–2) – последовательность Прюфера, N = {1, 2, ..., n}.
1. Выберем минимальное число v из N, не содержащееся в P.
2. Соединяем ребром вершину с номером v и вершину, соответствующую первому числу из P.
3. Удаляем v из N, удаляем первое число из P.
4. Если в N осталось два числа – соединяем ребром соответствующие вершины, иначе – п. 1.
Кодирование Прюфера задаёт взаимно-однозначное соответствие между множеством помеченных деревьев порядка n и множеством числовых последовательностей, состоящих из n – 2 натуральных чисел из набора {1,...,n}.
Пример
v Для кодирования дерева (рис. 2.20, а) применим алгоритм Прюфера, заполним последовательность
P = (p1, p2, p3, p4, p5, p6, p7, p8).
Выберем лист с минимальным номером – 2, в последователь-ность Прюфера добавляем номер смежной с этим листом вершины – 1. Тогда имеем:
P = (1, p2, p3, p4, p5, p6, p7, p8).
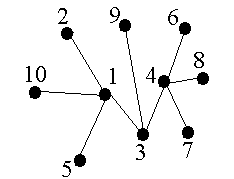
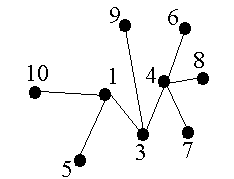
а б
Рис. 2.20. Применение алгоритма Прюфера. Упаковка дерева
Удаляем из дерева этот лист и инцидентное ребро (рис. 2.20, б). Подобным образом найдем следующий лист с минимальным номером – 5, в последовательность Прюфера добавляем 1:
P = (1, 1, p3, p4, p5, p6, p7, p8).
Повторяя данную процедуру, получим последовательность
(1,1,4,4,4,3,3,1).
Теперь распакуем дерево. Имеем последовательность Прюфера
(1,1,4,4,4,3,3,1),
содержащую 8 элементов, значит, восстанавливаемый граф будет содержать 10 вершин:
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Выберем минимальное число из N, не содержащееся в P, это число 2. Соединяем ребром лист с номером 2 и вершину 1, соответствующую первому числу из P (рис. 2.21, а), и удаляем из P число 1, из N – число 2. Снова выберем минимальное число из N, не содержащееся в P, это число 5. Соединяем ребром вершину с номером 5 и вершину 1, соответствующую второму числу из P
(рис. 2.21, б). Повторяем данную процедуру, пока не останется в N два числа 1 и 10, соединяем их ребром и получаем исходный граф (рис. 2.21, в).


а б в
Рис. 2.21. Применение алгоритма Прюфера. Распаковка дерева
2.6. Планарность, раскраска графов. Сети и потоки
& Определение.Изображение графа плоскостной диаграммой называется укладкой графа на плоскость.
Граф, изображенный на плоскости, называется плоским, если его ребра не пересекаются в точках, отличных от вершин графа.
Свойство «быть плоским» может не сохраняться при переходе к изоморфному графу. Принципиальный вопрос, на который нужно отвечать при решении задач типа прокладки коммуникаций, это имеет ли данный граф хотя бы одно плоское изображение? Определим класс графов, для которых ответ на этот вопрос положителен.
& Определения
Граф называется планарным, если он изоморфен плоскому графу, а его укладка – плоской реализацией планарного графа.
Конечная область, ограниченная простым циклом в плоском графе и не содержащая внутри себя других циклов, называется внутренней гранью плоской реализации графа.
Бесконечная область вне плоского графа называется внешней гранью плоской реализации графа.
Множество граничных точек грани называется ее краем.
Пример
v На рис. 2.22 оказан граф с 4 гранями.
Рис. 2.22. Плоский граф
& Формула Эйлера. Пусть G = (V, X) связный планарный граф,  ,
, 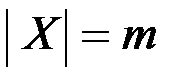 , тогда для любой геометрической реализации графа на плоскости справедлива формула
, тогда для любой геометрической реализации графа на плоскости справедлива формула
 ,
,
где r – число граней.
Если граф имеет k компонент связности:
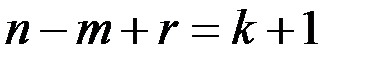 .
.
& Следствия
1. Формула Эйлера справедлива для геометрической реализации графа на сфере.
2. Для любого выпуклого многогранника
 .
.
& Теорема о связи числа ребер с длиной минимального цикла
Пусть G = (V, X) связный планарный граф, 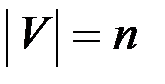 ,
, 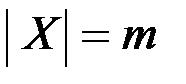 , в котором нет циклов длины меньше l (
, в котором нет циклов длины меньше l ( 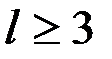 ), то
), то
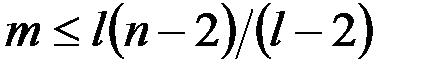 .
.
? Замечание. Если 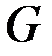 – простой связный планарный граф, то в нем нет циклов длины меньше трех, поэтому
– простой связный планарный граф, то в нем нет циклов длины меньше трех, поэтому
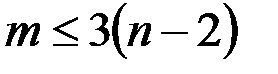 .
.
& Теорема о непланарности графов  и
и 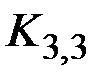
В графе 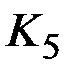
 . Если он планарен, то
. Если он планарен, то 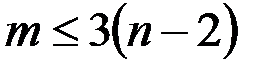 , т. е.
, т. е. 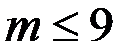 – противоречие.
– противоречие.
В графе 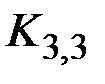
 . Если он планарен, то
. Если он планарен, то 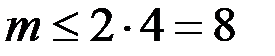 –противоречие.
–противоречие.
& Определения
Подразбиение ребра 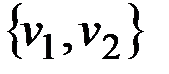 – удаление этого ребра, добавление новой вершины v к V и двух новых ребер
– удаление этого ребра, добавление новой вершины v к V и двух новых ребер  и
и 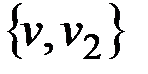 к множеству X.
к множеству X.
Стягивание смежных вершин – операция удаления ребра  и замена двух вершин
и замена двух вершин  и
и 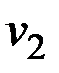 одной вершиной, которая соединяется ребрами со всеми вершинами графа, с которыми были смежны вершины
одной вершиной, которая соединяется ребрами со всеми вершинами графа, с которыми были смежны вершины  и
и  .
.
Граф G называется подразбиением графа G1, если он может быть получен из G путем конечного числа подразбиения ребер.
Из определения следует, что граф 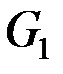 будет отличаться от графа
будет отличаться от графа  только вершинами степени 2.
только вершинами степени 2.
& Определение. Два графа G и H называются гомеоморфными, если они могут быть получены друг из друга с помощью операций подразбиения ребер или стягивания вершин степени 2.
Таким образом графы гомеоморфны, если существуют их подразбиения, которые изоморфны друг другу. Гомеоморфизм графов является отношением эквивалентности.
Пример
v На рис. 2.23 показана операция подразбиения ребра
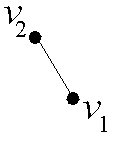
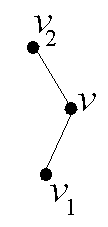
Рис. 2.23. Подразбиение ребра
v На рис. 2.24 показаны пары гомеоморфных графов.
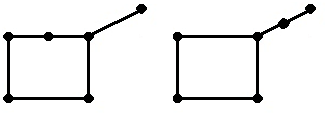
а б
Рис. 2.24. Гомеоморфные графы
Рассмотрим плоский граф G с пятью вершинами (рис. 2.25, а). Если добавить к нему ребра {1,3} и {1,5}, то полученный новый граф G (рис. 2.25, б) тоже будет плоским. К этому графу не удается добавить ни одного ребра так, чтобы новый граф тоже был плоским.

а б
Рис. 2.25. Гомеоморфные графы
& Определение. Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским.
Следовательно, граф на рис. 2.25, б – максимально плоский.
Каждая грань в плоском представлении максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф называют триангулированным.
& Определение. Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
& Определение. Двойственный граф G' к планарному графу G – это граф, в котором вершины соответствуют граням графа G; эти вершины соединены ребром, только если соответствующие им грани графа G имеют общее ребро.
Пример
v Двойственны друг к другу графы куба и октаэдра.
Поскольку двойственный граф зависит от способа укладки, к одному и тому же планарному графу могут существовать несколько двойственных (неизоморфных).
Также заметим, что каждому ребру, не входящему в цикл, в двойственном графе соответствует петля.
Пример
v На рис. 2.26 показаны графы (сплошной линией) и двойственные к ним (пунктирной линией). На рис. 2.26, б двойственные графы не изоморфны, поскольку верхний имеет степень 6 (внешняя грань). На рис. 2.26, в показано дерево и двойственный к нему граф, который имеет только одну вершину и петли, количество которых равно количеству ребер дерева.
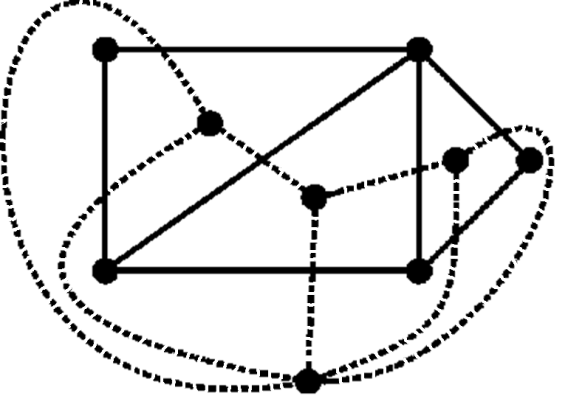
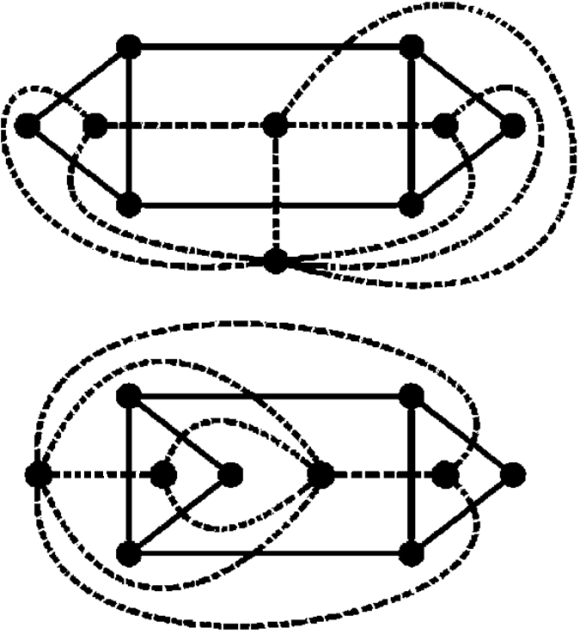
а б
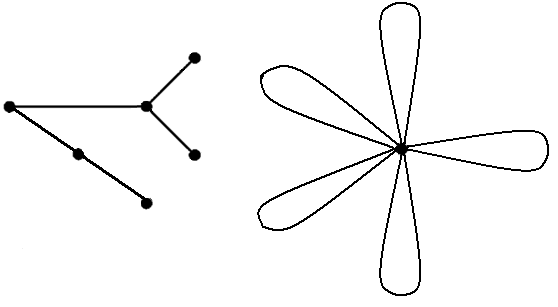
в
Рис. 2.26. Двойственные графы (а); неизоморфные двойственные графы (б); дерево и двойственный ему граф (в)
& Критерии планарности графов
1) Уитни: граф планарен, если у него есть двойственный.
2) Понтрягина – Куратовского: граф планарен тогда и только тогда, когда не содержит подграфов, гомеоморфных K5и K3,3 (т. е. в нем нет подграфов, полученных подразбиением ребер из K5и K3,3).
3) Вагнера: граф планарен тогда и только тогда, когда у него нет подграфов, стягиваемых к K5или K3,3.
Пример
v Рассмотрим граф Петерсена (рис. 2.27), он не содержит подграфа, изоморфного K5и K3,3, однако он не планарный, что следует из критерия Вагнера: граф приводится к графу K5 после стягивания ребер r1, r2, r3, r4, r5.
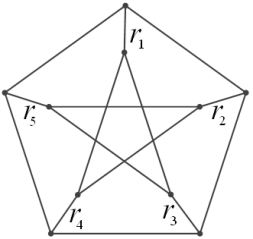
Рис. 2.27. Граф Петерсена
v Покажем, что граф на рис. 2.28, а непланарен: для этого выделим подграф (рис. 2.28, б), который гомеоморфен графу K3,3 (рис. 2.28, в).
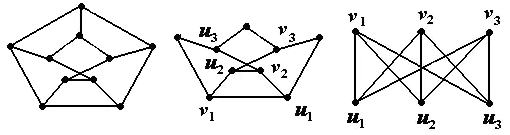
а б в
Рис. 2.28. Пример непланарного графа
? Замечание.Любой конечный граф допускает геометрическую реализацию в трехмерном пространстве.
Доказательство. Пусть 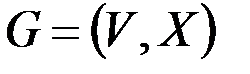 ,
, 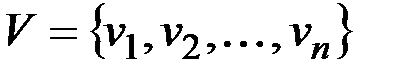 ,
, 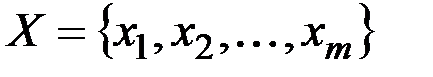 . Проведем в трехмерном пространстве прямую, на которой отложим точки
. Проведем в трехмерном пространстве прямую, на которой отложим точки  , через эту прямую проведем
, через эту прямую проведем  полуплоскостей, и каждую кривую
полуплоскостей, и каждую кривую 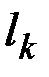 , соответствующую ребру
, соответствующую ребру 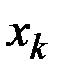 , расположим в своей полуплоскости. Получим геометрическую реализацию графа.
, расположим в своей полуплоскости. Получим геометрическую реализацию графа.
Раскраска графов
& Определение. Раскраска графа – это разбиение элементов графа на множества (называемые цветами). Обычно цвета – это числа
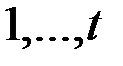 . Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения на множестве
. Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения на множестве 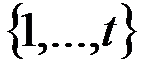 .
.
Множество объектов, окрашенных в один цвет, называется одноцветным классом.
& Определение. Правильная раскраска вершин в t цветов – это разбиение V=V1ÈV2È…ÈVt такое, что 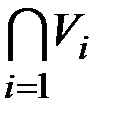 =Æ,
=Æ,  , но каждое из Vi не пусто, при этом случае никакие две смежные вершины не раскрашены в один цвет.
, но каждое из Vi не пусто, при этом случае никакие две смежные вершины не раскрашены в один цвет.
Граф называется t-раскрашиваемым, если его можно правильно раскрасить t цветами.
Наименьшее число из t при условии правильности раскраски называется хроматическим числом χ(G).
Пример
v Граф Kn – n-хроматический, любой двудольный граф, а также любое дерево – 2-хроматические.
Если в графе G = (V, X)  , то граф не более чем
, то граф не более чем
(t+1)-раскрашиваем. Любой планарный граф без петель не более чем 5-раскрашиваем.
& Определение. Правильная раскраска ребер в g цветов – это разбиение множества ребер X=X1ÈX2È….ÈXg, где 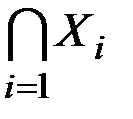 =Æ,
=Æ, 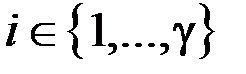 и каждое Xi образует паросочетание (произвольное подмножество попарно несмежных ребер графа) в G, т. е. никакие два смежных ребра не получают в ней одинакового цвета.
и каждое Xi образует паросочетание (произвольное подмножество попарно несмежных ребер графа) в G, т. е. никакие два смежных ребра не получают в ней одинакового цвета.
Наименьшее из g при условии правильности раскраски называется хроматическим индексом g(G).
Для хроматического индекса справедливы верхняя и нижняя оценки:
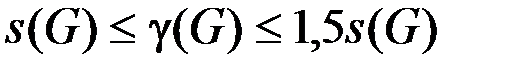 ,
, 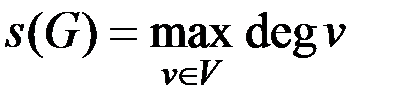 ,
,
где 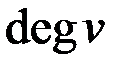 – степень вершины v.
– степень вершины v.
Раскраска, при которой окрашиваются и вершины, и ребра, а правильность означает принадлежность двух инцидентных элементов различным одноцветным классам, называется тотальной раскраской в t цветов. Наименьшее число цветов составляет тотальный минимум.
Раскраска называется свободной, если не все цвета из множества цветов используются.
Две такие раскраски различны, если два используемых набора цветов различаются хотя бы одним цветом.
Пример
v На рис. 2.29 показаны различные раскраски.
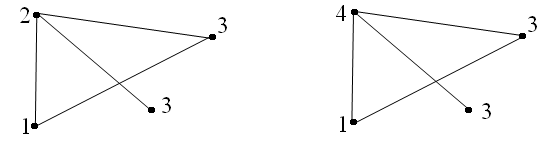
Рис. 2.29. Раскраска графов
& Определение. Граф называется критическим, если
 и
и 
для любого x из множества X .
Правильная раскраска ребер графа в 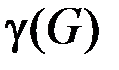 –1 цветов называется напряженной, если одно ребро остается не раскрашенным.
–1 цветов называется напряженной, если одно ребро остается не раскрашенным.
Если t(G)=2, то  =s(G). При этом в графе существует паросочетание, охватывающее все вершины наибольшей степени.
=s(G). При этом в графе существует паросочетание, охватывающее все вершины наибольшей степени.
Теорема о 4 красках
Данная теорема утверждает, что всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. При этом области могут быть как односвязными, так и многосвязными (в них могут присутствовать «дырки»), а под общим участком границы понимается часть линии, т. е. стыки нескольких областей в одной точке общей границей для них не считаются.
Эта теорема была сформулирована Фрэнсисом Гутри в 1852 г., однако доказать ее долгое время не удавалось. В течение этого времени было предпринято множество попыток как доказательства, так и опровержения, и эта задача носила название проблемы четырех красок. Задача раскраски карты на плоскости эквивалентна задаче на сфере.
Для простых карт достаточно и трех цветов, а четвертый цвет начинает требоваться, например, тогда, когда имеется одна область, окруженная нечетным числом других, которые соприкасаются друг с другом, образуя цикл.
Теорема о пяти красках, утверждающая, что достаточно пяти цветов, имела короткое несложное доказательство и была доказана в конце XIX в., но доказательство теоремы для случая четырех цветов столкнулось со значительными трудностями.
Теорема о четырех красках была доказана в 1976 г. К. Аппелем и В. Хакеном из Иллинойского университета. Это была первая крупная математическая теорема, доказанная с помощью компьютера. Первым шагом доказательства была демонстрация того, что существует определенный набор из 1936 карт, ни одна из которых не может содержать карту меньшего размера, которая опровергала бы теорему. Аппель и Хакен использовали специальную компьютерную программу, чтобы доказать это свойство для каждой из 1936 карт. Доказательство этого факта заняло сотни страниц. После этого Аппель и Хакен пришли к выводу, что не существует наименьшего контрпримера к теореме, потому что иначе он должен бы содержать, хотя не содержит, какую-нибудь из этих 1936 карт. Это противоречие говорит о том, что вообще не существует контрпримера. Изначально доказательство не было принято всеми математиками, поскольку его невозможно было проверить вручную. В дальнейшем оно получило более широкое признание, хотя у некоторых долгое время оставались сомнения.
Чтобы развеять оставшиеся сомнения, в 1997 г. Робертсон, Сандерс, Сеймур и Томас опубликовали более простое доказательство, использующее аналогичные идеи, но по-прежнему проделанное с помощью компьютера. Кроме того, в 2005 г. доказательство было проделано Д.Гонтиром с использованием специального программного обеспечения (Coq v7.3.1).
Паросочетания
Как было сказано выше, паросочетанием называется произвольное подмножество попарно несмежных ребер двудольного графа.
Пример
v Для графа, изображенного на рис. 2.30, паросочетанием будет, например, множество  .
.
Рассмотрим 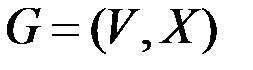 – двудольный граф,
– двудольный граф,  , где
, где 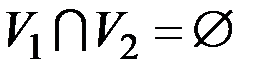 , Пусть
, Пусть 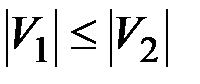 , тогда введем понятие совершенного паросочетания.
, тогда введем понятие совершенного паросочетания.
& Определение. Паросочетание будет совершенным, если в подмножество попарно несмежных ребер вошли все вершины множества 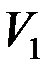 .
.
Пример
v Для графа, приведенного на рис.2.30, совершенным паросочетанием будет, например, множество
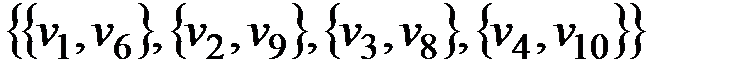 .
.
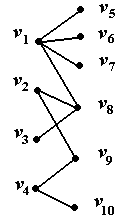
Рис. 2.30. Двудольный граф с совершенным паросочетанием
С совершенными паросочетаниями связано много прикладных задач, например, задача о составлении расписаний, задача о назначении на должность. Пусть 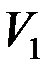 – множество должностей,
– множество должностей, 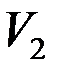 – множество претендентов, ребро
– множество претендентов, ребро 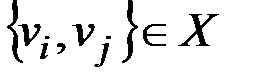 , если
, если 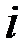 -ю должность может занимать
-ю должность может занимать  -й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания.
-й претендент, тогда назначение претендентов на должности есть построение совершенного паросочетания.
Построить совершенное паросочетание удается не всегда
(рис. 2.31).
Критерий существования совершенного паросочетания сформулировал и доказал Холл в 1935 г., он известен как теорема Холла, в основе которой лежит задача о свадьбах.
Пусть есть 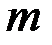 юношей и
юношей и  девушек,
девушек, 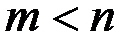 . Каждый из юношей знаком с какими-то девушками. Спрашивается, всегда ли можно женить этих юношей на знакомых им девушках?
. Каждый из юношей знаком с какими-то девушками. Спрашивается, всегда ли можно женить этих юношей на знакомых им девушках?
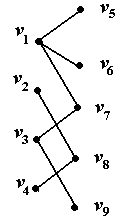
Рис. 2.31. Двудольный граф без совершенного паросочетания
На языке теории графов задачу можно сформулировать так: пусть 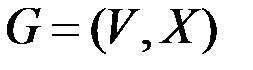 – двудольный граф,
– двудольный граф,  , где
, где  , где
, где 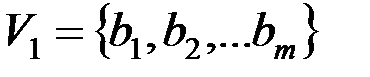 – множество юношей,
– множество юношей, 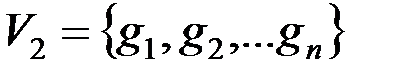 – множество девушек, если
– множество девушек, если  -й юноша знаком с
-й юноша знаком с  -й девушкой, то существует ребро
-й девушкой, то существует ребро  . Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
. Женить всех юношей на знакомых им девушках означает построить совершенное паросочетание в графе.
Решение задачи о свадьбах существует тогда и только тогда, когда любые 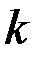 юношей из
юношей из  знакомы в совокупности не менее чем с
знакомы в совокупности не менее чем с 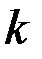 девушками
девушками 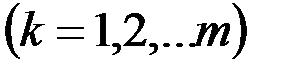 .
.
? Замечание. Если  , это означает, что любая группа
, это означает, что любая группа 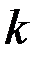 юношей числом меньше
юношей числом меньше 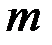 знакома не менее чем с
знакома не менее чем с 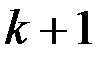 девушкой и только ровно
девушкой и только ровно  юношей знакомы с
юношей знакомы с 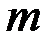 девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается
девушками. Тогда берем любого юношу, женим на знакомой девушке. Остается  юноша, из которых любые
юноша, из которых любые 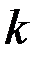 знакомы не менее чем с
знакомы не менее чем с 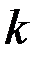 девушками.
девушками.
& Теорема Холла. Построить совершенное паросочетание в графе можно тогда и только тогда, когда любые 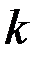 вершин множества
вершин множества 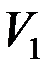 смежны в совокупности не менее чем с
смежны в совокупности не менее чем с 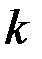 вершинами множества
вершинами множества  .
.
Для графа на рис. 2.31 условие теоремы Холла не выполняется: вершины 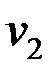 и
и  смежны только с одной вершиной
смежны только с одной вершиной 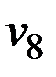 .
.
Сети и потоки
Сеть можно представить как систему, транспортирующую некий продукт из одной точки в другую (электроэнергия, природный газ, нефть и др.). Рассмотрим сеть как орграф, дуги которого – трубы между точками системы (вершинами графа).
Положительное число, соответствующее каждой дуге графа, называется пропускной способностью.
Если между двумя вершинами не существует дуги, то пропускная способность равна нулю. В примере с нефтяными сетями пропускная способность связана с количеством нефти, проходящей через трубу (дугу).
Наличие петель у графа недопустимо, поскольку рассматриваемые задачи связаны только с транспортировкой продукта между различными точками. Будем считать, что если существует дуга из v i в v j, то нет дуги из v j в v i. Таким образом, рассматривается поток продукта только в одну сторону.
Рассмотрим также особую вершину a, называемую источником, и особую вершину z, называемую стоком.
Полустепень захода вершины a равна 0, так что в источник ничто не втекает.
Полустепень исхода вершины z равна 0, так что из стока ничто не вытекает. Таким образом, продукт перевозится из a в z.
Для сети вводится понятие потока: для каждой дуги имеется значение, которое является потоком через конкретную дугу. Очевидно, величина потока не может превышать пропускную способность дуги. Требуется также, чтобы поток, входящий в вершину, был равен потоку, выходящему из вершины, за исключением вершин a и z. Данное правило называется сохранением потока.
& Определение. Орграф, в котором каждая дуга имеет положительную пропускную способность и поток, называется транспортной сетью.
Дуга называется насыщенной, если ее поток равен ее пропускной способности.
Пример
v На рис. 2.32 показан пример потока в сети, где первый элемент на каждой дуге – пропускная способность, а в скобках – поток.
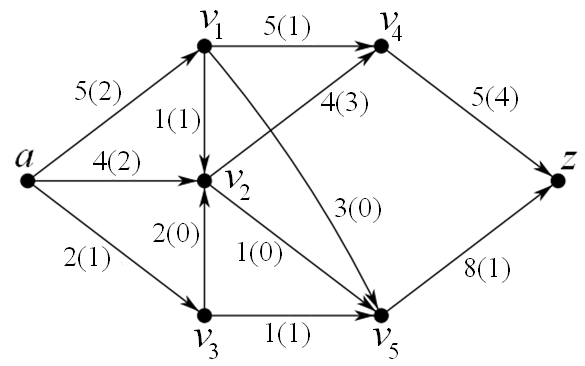
Рис. 2.32. Пример сети
& Определение. Разрез графа – это такая пара множеств вершин (V1,V2), что V=V1ÈV2,  ,
,  ,
,  . Величиной разреза называется сумма пропускных способностей таких дуг (v i, v j), что
. Величиной разреза называется сумма пропускных способностей таких дуг (v i, v j), что  ,
,  .
.
Минимальный разрез – разрез с минимальной пропускной способностью.
& Теорема Форда–Фалкерсона.Величина максимального потока в графе равна величине пропускной способности его минимального разреза.
Доказательство (достаточность). Любой поток между вершинами v i и v j меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин продуктов, перевозимых по всем возможным путям из вершины v i в v j. Каждый такой путь обязан иметь общую дугу с данным сечением. Так как по каждой дуге сечения суммарно нельзя перевести продукта больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна сумме всех пропускных способностей дуг данного сечения.
2.7. Некоторые алгоритмы теории графов
Выделение компонент сильной связности орграфа
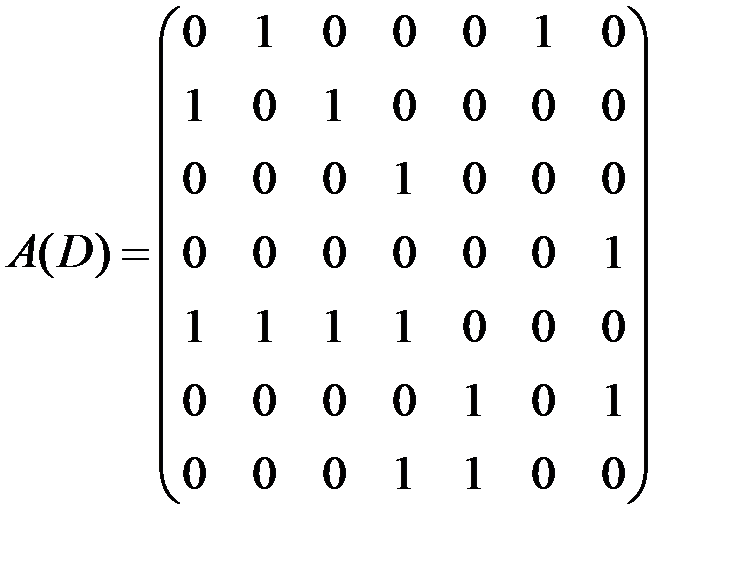
С помощью матрицы смежности найти компоненты сильной связности орграфа D .
Cоставляем матрицу смежности A(D) для данного орграфа: она состоит из нулей и единиц, номера строк – индексы вершин, из которых исходят дуги, номера столбцов – индексы вершин, в которые дуги входят. Если есть дуга, исходящая из вершины vi и входящая в vj, то элемент матрицы смежности, стоящий на пересечении i-й строки и j-го столбца равен 1, иначе – 0.
Для выделения компоненты сильной связности, необходимо сначала найти матрицу достижимости T(D) орграфа по первой формуле утверждения 3, затем матрицу сильной связности S(D) (она должна быть симметрической) по второй формуле из того же утверждения.
Алгоритм выделения компонент сильной связности
1. Присваиваем p=1 (p – количество компонент сильной связности),  .
.
2. Включаем во множество вершин Vp компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp . В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p – количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как Sp+1, присваиваем p=p+1 и переходим к п. 2.
Пример
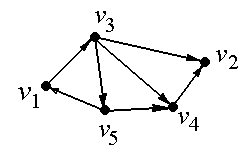
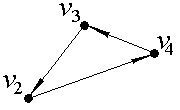
v Выделим компоненты сильной связности орграфа, изображенного на рис.2.33.
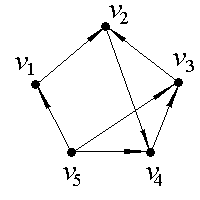
Рис. 2.33. Пример орграфа для нахождения компонент сильной связности
n=5, значит, матрица смежности 5×5 и будет выглядеть так
 .
.
По формуле из утверждения 3 найдем матрицу достижимости T(D):
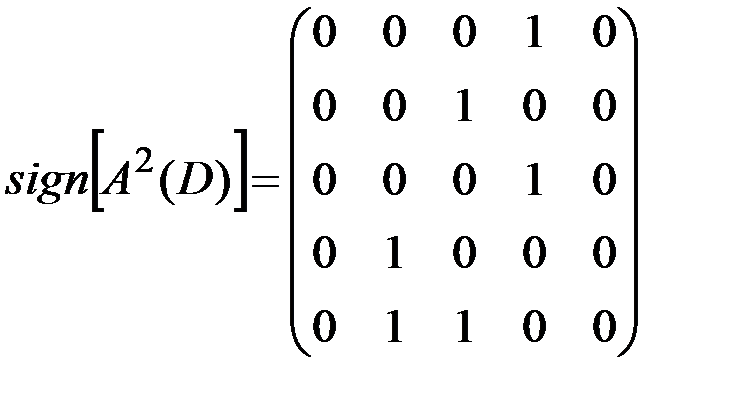 ,
, 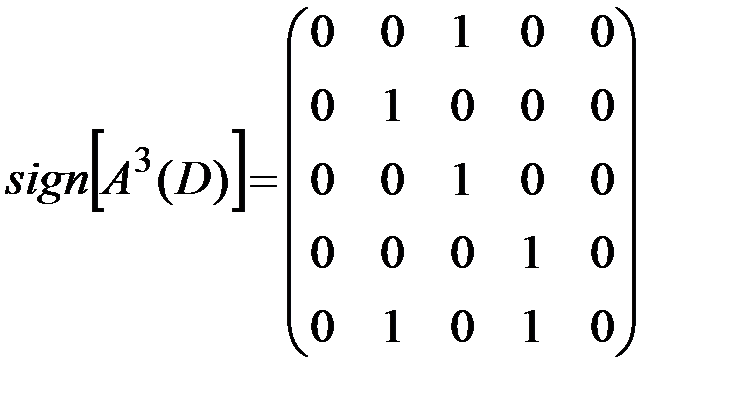 ,
,
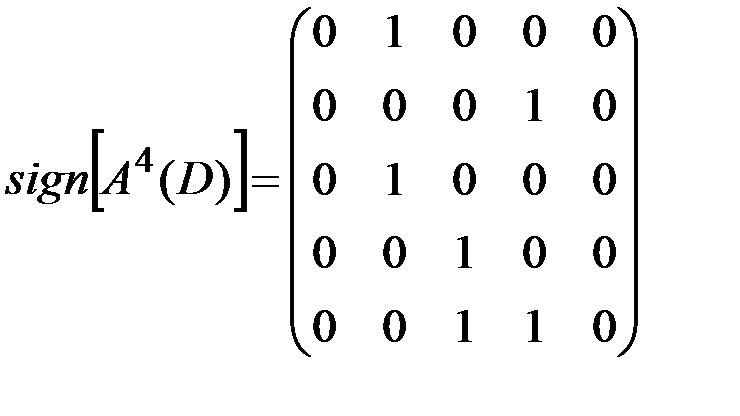 .
.
Следовательно,
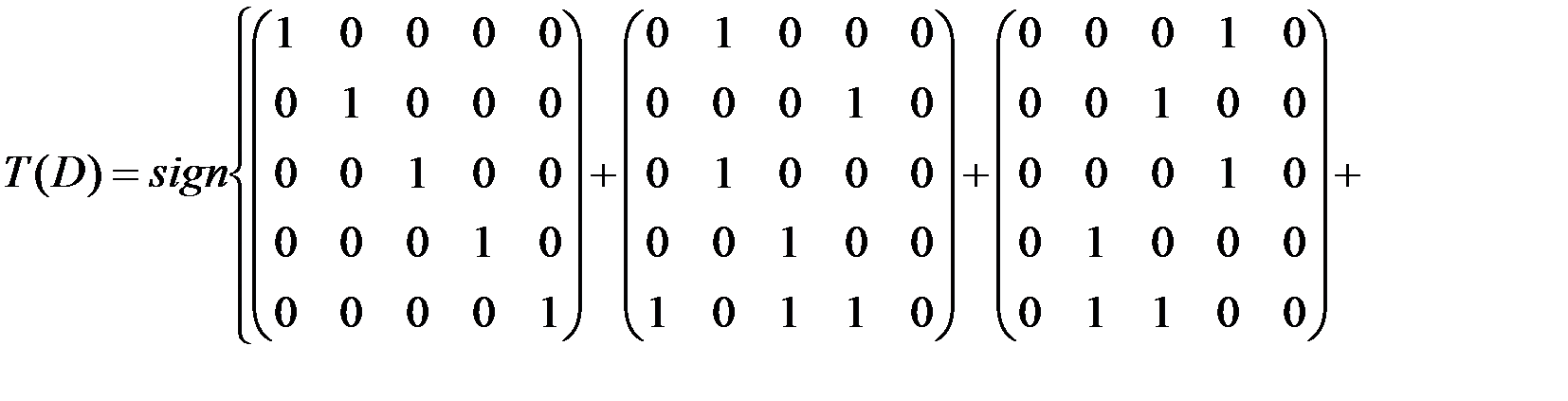
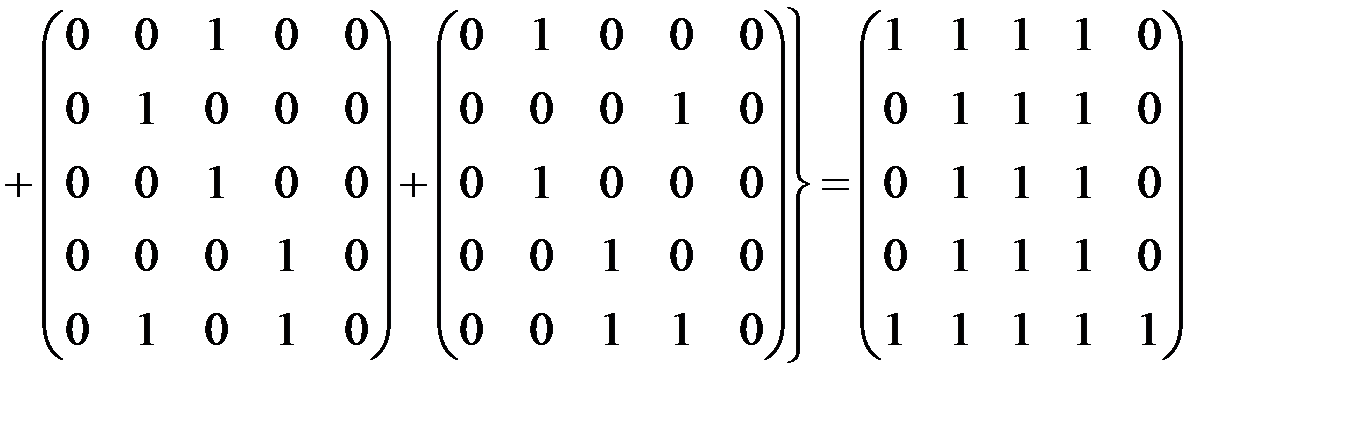 .
.
Таким образом, матрица S(D), также полученная из утверждения 3, будет следующей:
 .
.
Присваиваем p=1, 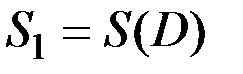 и составляем множество вершин первой компоненты сильной связности D1: это вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины
и составляем множество вершин первой компоненты сильной связности D1: это вершины, которым соответствуют единицы в первой строке матрицы S(D). Таким образом, первая компонента сильной связности состоит из одной вершины 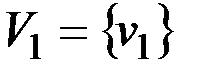 .
.
Вычеркиваем из матрицы S1(D) строку и столбец, соответствующие вершине v1, и получаем матрицу S2(D):
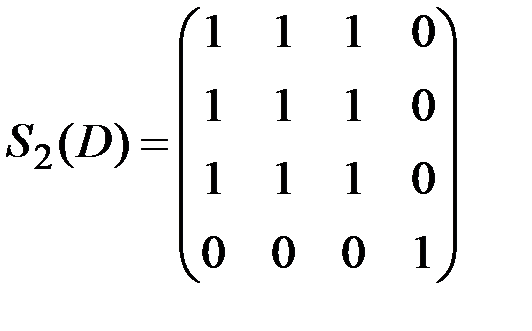 .
.
Присваиваем p=2. Множество вершин второй компоненты связности составят вершины, которым соответствуют единицы в первой строке матрицы S2(D), т.е. 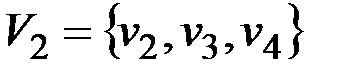 .
.
Составляем матрицу смежности для компоненты сильной связности  исходного графа D – в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
исходного графа D – в ее качестве возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V2:
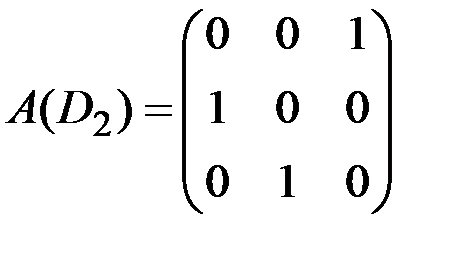 .
.
Вычеркиваем из матрицы S2(D) строки и столбцы, соответствующие вершинам из V2, и получаем матрицу S3(D), которая состоит из одного элемента:
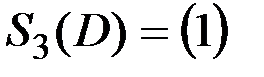 ,
,
и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины  .
.
Таким образом, выделены три компоненты сильной связности орграфа D (рис. 2.34).
D1:
| D2:
| D3:
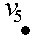
|
Рис. 2.34. Компоненты сильной связности
Расстояния в орграфе
Найти расстояния в орграфе D : диаметр, радиус и центры, а также с помощью алгоритма фронта волны найти минимальный путь из вершины v в w .
Пусть 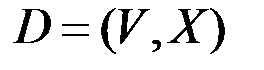 орграф с n³2 вершинами и v,w (v¹w) – заданные вершины из V.
орграф с n³2 вершинами и v,w (v¹w) – заданные вершины из V.
Для нахождения метрических характеристик графа необходимо составить матрицу минимальных расстояний M(D)=[mij]. Это квадратная матрица размерности 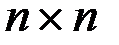 , элементы главной диагонали которой равны нулю (
, элементы главной диагонали которой равны нулю ( 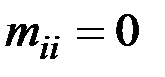 , i=1,..,n). Для заполнения остальных элементов составляем матрицу A(D) и переносим единицы из нее в матрицу M(D) (
, i=1,..,n). Для заполнения остальных элементов составляем матрицу A(D) и переносим единицы из нее в матрицу M(D) ( 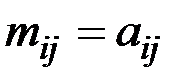 , если
, если 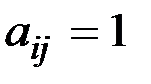 ). Далее построчно заполняем матрицу следующим образом.
). Далее построчно заполняем матрицу следующим образом.
Рассматриваем первую строку матрицы M(D), в которой есть единицы, пусть это элемент 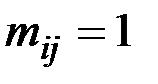 . Значит, из вершины
. Значит, из вершины  можно попасть в вершину
можно попасть в вершину 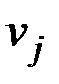 за один шаг. Рассматриваем j-ю строку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент
за один шаг. Рассматриваем j-ю строку (строку стоит вводить в рассмотрение, если она содержит хотя бы одну единицу). Пусть элемент  . Тогда из вершины
. Тогда из вершины 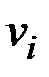 в вершину
в вершину 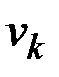 можно попасть за два шага. Таким образом, можно записать в матрицу M(D)
можно попасть за два шага. Таким образом, можно записать в матрицу M(D) 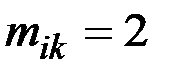 .
.
Следует заметить, что если в рассматриваемых строках две или более единиц, то необходимо прорабатывать все возможные варианты попадания из одной вершины в другую, записывая в матрицу M(D) длину наикратчайшего из них.
После заполнения матрицы M(D) применяются формулы подглавы 2.5 для нахождения диаметра, эксцентриситета, центров и радиуса графа.
Алгоритм фронта волны
1. Помечаем вершину v индексом 0, затем помечаем вершины Î образу вершины v, индексом 1. Обозначаем их FW1 (v). Полагаем k=1.
2. Если  или k=n–1 и одновременно
или k=n–1 и одновременно 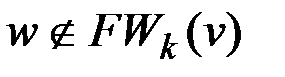 , то вершина w не достижима из v. Работа алгоритма заканчивается. В противном случае продолжаем.
, то вершина w не достижима из v. Работа алгоритма заканчивается. В противном случае продолжаем.
3. Если 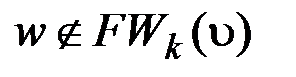 , то переходим к шагу 4. В противном случае мы нашли минимальный путь из v в w и его длина равна k. Последовательность вершин
, то переходим к шагу 4. В противном случае мы нашли минимальный путь из v в w и его длина равна k. Последовательность вершин
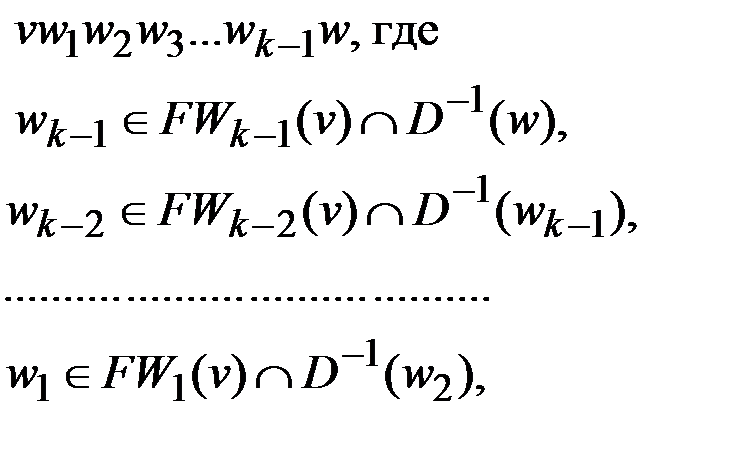
есть этот минимальный путь. Работа завершается.
4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин c индексом k. Множество вершин с индексом k+1 обозначаем  . Присваиваем k:=k+1 и переходим к шагу 2.
. Присваиваем k:=k+1 и переходим к шагу 2.
? Замечания
ü Множество 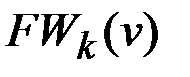 называется фронтом волны k -го уровня.
называется фронтом волны k -го уровня.
ü Вершины  могут быть выделены неоднозначно, что соответствует случаю, если существует несколько минимальных путей из v в w.
могут быть выделены неоднозначно, что соответствует случаю, если существует несколько минимальных путей из v в w.
Пример
v Найдем расстояния в орграфе D (рис.2.35). n=7, значит, матрицы A(D) и M(D)будут иметь размерность 7×7.
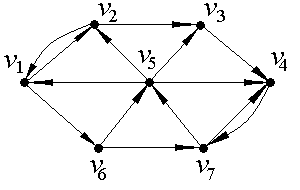
Рис. 2.35. Пример орграфа для нахождения метрических характеристик
и минимального расстояния
Матрица смежности:
 .
.
Начинаем заполнять матрицу M(D): ставим нули по главной диагоналии mij=aij, если aij=1, (т.е. переносим единицы из матрицы смежности). Рассматриваем первую строку. Здесь есть две единицы, т.е. из первой вершины за один шаг можно попасть во вторую и шестую. Из второй вершины можно попасть за один шаг в третью (путь в первую вершину нас не интересует), следовательно, необходимо записать m13=2. Из шестой вершины можем добраться за один шаг в пятую и седьмую, а значит, m15=2, m17=2. Подобным образом находим все пути за 2 шага и расставляем все двойки в матрицу M(D).
Теперь ищем маршруты, исходящие из первой вершины, состоящие из 3 шагов: за 2 шага идем в третью вершину, оттуда за один шаг попадаем в четвертую, поэтому m14=3. Заполняем все тройки, затем четверки и т. д., пока не заполним всю матрицу M(D).
В итоге получим следующую матрицу:
 .
.
Согласно формулам подглавы 2.5 и матрице M(D) диаметр орграфа равен 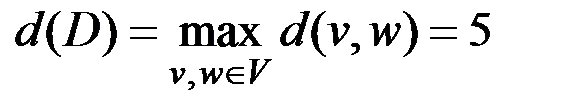 .
.
Для каждой вершины орграфа по матрице M(D) найдем максимальное удаление (эксцентриситет) от данной вершины с помощью формулы  : r(vi) – максимальное из расстояний, стоящих в i-й строке. Имеем
: r(vi) – максимальное из расстояний, стоящих в i-й строке. Имеем
r(v1)=3, r(v2)=3, r(v3)=5, r(v4)=4, r(v5)=2, r(v6)=2, r(v7)=3.
Значит, радиусорграфа равен  .
.
Соответственно, центрами орграфабудут вершины v5 и v6, так как величины их эксцентриситетов совпадают с величиной радиуса  .
.
Опишем теперь нахождение минимального пути между наиболее удаленными вершинами (из вершины v3 в вершину v6) по алгоритму фронта волны. Обозначим вершину v3 как V0, а вершину v6 - как W (рис.2.36).
Множество вершин, принадлежащих образу V0, состоит из одного элемента - это вершина v4, которую, согласно алгоритму, обозначаем как V1: FW1(v3) ={v4}.
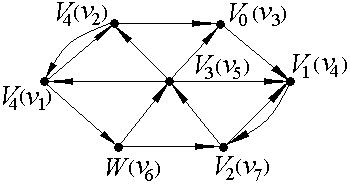
Рис. 2.36. Применение алгоритма фронта волны для нахождения минимального пути в орграфе
Поскольку искомая вершина не принадлежит фронту волны первого уровня  , то продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V1: FW2(v3) ={v7}, обозначаем v7≡V2. В образ вершины V2 входят две вершины - v5 и v4, но, так как v4 уже была помечена как V1, то фронт волны третьего уровня состоит из одного элемента: FW3(v3)={v5}, v5≡V3. Из непомеченных вершин в образ вершины V3 входят v1 и v2, соответственно, FW4(v3)={v1, v2}, v1≡V4, v2≡V4.
, то продолжаем работу алгоритма. Строим фронт волны второго уровня - это множество вершин, принадлежащих образу вершины V1: FW2(v3) ={v7}, обозначаем v7≡V2. В образ вершины V2 входят две вершины - v5 и v4, но, так как v4 уже была помечена как V1, то фронт волны третьего уровня состоит из одного элемента: FW3(v3)={v5}, v5≡V3. Из непомеченных вершин в образ вершины V3 входят v1 и v2, соответственно, FW4(v3)={v1, v2}, v1≡V4, v2≡V4.
Теперь помечены все вершины, кроме v6, которая входит в образ вершины  , т.е. FW5(v3)={v6≡W}, работа алгоритма закончена.
, т.е. FW5(v3)={v6≡W}, работа алгоритма закончена.
Минимальный путь (5 шагов) из вершины v3 в вершину v6:
v3 v4 v7 v5 v1 v6.
2.7.3. Поиск метрических характеристик транспортной сети
Алгоритмы быстрого поиска
Метрические характеристики (центр, радиус и диаметр) являются существенными свойствами графов и дают важную информацию о реальных структурах, представляемых ими. Например, в задачах размещения центр и радиус могут соответствовать наилучшему местоположению пункта обслуживания и максимально необходимому времени, чтобы добраться до него. В тех случаях, когда графы представляют вычислительные сети, диаметр может обозначать время прохождения сигнала между двумя узлами с наиболее медленным соединением, а радиус указывать на задержку между сервером и самым медленным клиентом и т. д. Далее рассматриваются задачи поиска метрических характеристик для неориентированных графов, предлагаются алгоритмы, разработанные Тимеряевым Т.В. и Ураковым А.Р.
Постановка задачи
Рассматриваются задачи двух типов.
Задача 1: нахождение центра, радиуса и диаметра графа, заданного лишь множествами вершин V и ребер Х.
Задача 2: нахождение центра, радиуса и диаметра графа при наличии дополнительной информации в виде вычисленной в следующем разделе матрицы кратчайших расстояний М между всеми парами вершин графа.
Заметим, что задача 2 решается намного быстрее, чем расчет матрицы минимальных расстояний M. Поэтому далее в большей мере рассматривается задача 1.
Рассматривается связный неориентированный нагруженный граф G=(V,X,U), заданный множествами вершин, ребер и весовых значений. Мощности множества вершин и множества ребер будем считать равными |V|=n, |X|=m.
Вес ребра, соединяющего вершины 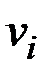 и vj –
и vj –  . Вес пути – сумма весов входящих в него ребер. Значение элемента матрицы минимальных расстояний
. Вес пути – сумма весов входящих в него ребер. Значение элемента матрицы минимальных расстояний  – наименьшее значение из возможных весов путей, соединяющих вершины
– наименьшее значение из возможных весов путей, соединяющих вершины  и
и 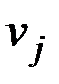 . Очевидно, что граф может иметь несколько центров и несколько пар периферийных вершин.
. Очевидно, что граф может иметь несколько центров и несколько пар периферийных вершин.
Для решения задачи 1 зададимся целью нахождения хотя бы одного из центров, одной пары периферийных вершин, радиуса и диаметра для данного графа. Центр графа образует связный подграф, поэтому, если найдена одна из центральных вершин графа, все оставшиеся могут быть выявлены поиском в ширину (метод обхода графа и поиска пути в графе, работает путем последовательного просмотра отдельных уровней графа, начиная с узла-источника) из найденной. Поиск в ширину продолжается только из тех вершин, чей эксцентриситет равен радиусу графа.
Будем называть множеством опорных вершин 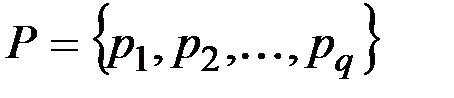 данного графа множество любых q вершин, информация о расстояниях от которых используется при вычислении метрических характеристик.
данного графа множество любых q вершин, информация о расстояниях от которых используется при вычислении метрических характеристик.
Основная идея данных алгоритмов состоит в следующем. Вначале определенным образом выбирается некоторое количество опорных вершин, и вычисляются от них расстояния до всех остальных вершин. Эта информация используется для определения метрических характеристик. Находятся границы интервалов неопределенности (нижние и верхние оценки) для радиуса и диаметра на данной итерации. После этого из рассмотрения выбрасываются вершины, расстояния от которых не входят в найденные границы. Если в рассмотрении остались вершины, число опорных вершин увеличивается, и снова определяются границы интервалов неопределенности для радиуса и диаметра. Процесс продолжается до тех пор, пока нижние и верхние оценки не совпадут. Полученные при этом значения радиуса и диаметра являются искомыми характеристиками.
Метод и алгоритм поиска центра и радиуса транспортной сети
В основе алгоритма лежит предположение о том, что центры реальных графов, вероятно, расположены вблизи их геометрических центров (рис. 2.37), и, следовательно, поиск центральных вершин нужно осуществлять среди вершин, лежащих в некоторой окрестности геометрического центра графа. В поставленной задаче исходный граф задан лишь тройкой G=(V,X,U) без дополнительных сведений о расположении вершин относительно друг друга в виде координат.
Этот факт исключает непосредственное нахождение геометрического центра графа, однако его приближение может быть найдено с использованием информации о расстояниях между вершинами.
Если данное эвристическое предположение не верно, то это приведет только к увеличению числа итераций. Но поскольку в практических задачах обычно это предположение справедливо, то достигается существенное ускорение получения решения (параграф 2.7.4).
В качестве начального приближения геометрического центра графа можно было бы использовать вершину, чье максимальное удаление  от периферийных вершин графа T минимально. Однако нахождение всех периферийных вершин графа или даже их пары (поиск диаметра графа) является задачей сопоставимой по сложности с поиском центра графа. Значит, приближены должны быть и периферийные вершины графа.
от периферийных вершин графа T минимально. Однако нахождение всех периферийных вершин графа или даже их пары (поиск диаметра графа) является задачей сопоставимой по сложности с поиском центра графа. Значит, приближены должны быть и периферийные вершины графа.
На рис. 2.38 показано, что вместо периферийных вершин в алгоритме используется множество опорных вершин P – вершин находящихся «по краям» графа. Первые два элемента множества P определяются как вершины p1 и p2, которые максимально удалены друг от друга: m(p1,p2)=ε(p1)=ε(p2). При этом первое приближение к центу графа ищется как вершина c1 минимально удаленная от p1 и p2.

Рис. 2.37. Пример расположения центров в реальном графе. Геометрический центр (центроид) отмечен крестом, центральная вершина – кругом
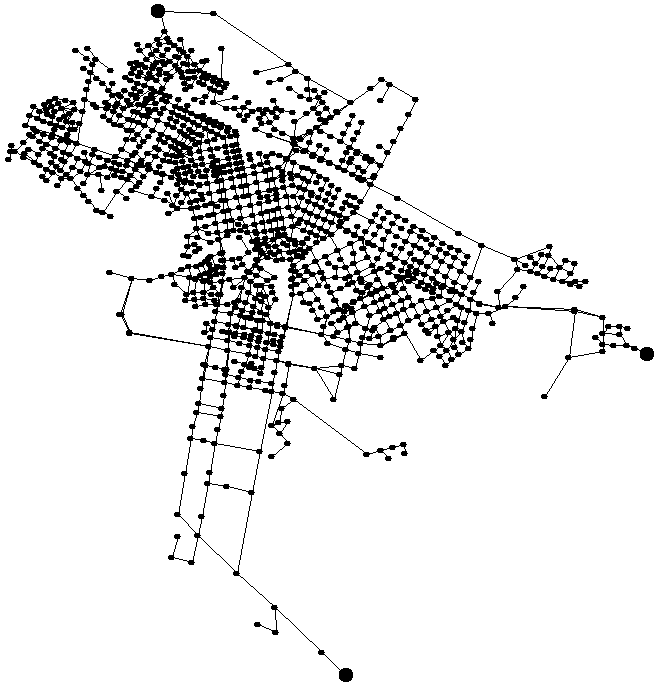
Рис. 2.38. Некоторые из возможных опорных вершин графа
(выделены жирными точками)
Рис 2.39 иллюстрирует пример выбора этих вершин. На основе вычисленных для c1 кратчайших расстояний уточняются оценки верхней и нижней границ радиуса и проверяется их равенство: rl=ru. Если равенство выполнено, вершина c1 является центром и поиск завершен. Иначе добавляем еще одну периферийную вершину – максимально удаленную от текущего претендента: p3: m(p3,c1)=ε(c1).
Рис. 2.39. Первая итерация алгоритма поиска центра и радиуса,
p1 и p2 – опорные вершины, c1 – первый претендент на центральную вершину
Множество опорных вершин P теперь содержит больше элементов и следующий претендент на центр c2, определяемый как наименее удаленный от тройки вершин p1, p2 и p3, будет (вероятно) более близок к центру графа. Рис. 2.40 иллюстрирует вторую итерацию алгоритма

Рис. 2.40. Вторая итерация алгоритма поиска центра и радиуса.
p1, p2 и p3 – опорные вершины, c2 – второй претендент, более точное приближение центральной вершины графа
В конечном итоге этот итеративный процесс приведет к нахождению центральной вершины графа. Далее описывается алгоритм поиска центра и радиуса более формально.
В основе алгоритма лежит определение нижней rl и верхней ru оценок радиуса графа. Просмотр вершин-претендентов на центр ci производится до тех пор, пока для какого-то из них не будет выполнено равенство этих границ rl=ru.
Для радиуса графа r и произвольной вершины vi справедливо 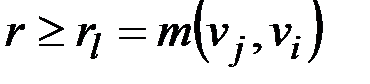 , где
, где  . Нижнюю границу радиуса rl также можно определить, используя множество опорных вершин P:
. Нижнюю границу радиуса rl также можно определить, используя множество опорных вершин P:
 .
.
В этом случае
 ,
,
где  – эксцентриситет центра графа
– эксцентриситет центра графа  .
.
С другой стороны, радиус графа r ограничен сверху эксцентриситетом любой вершины 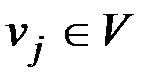 ,
, 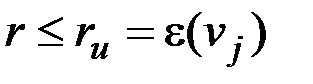 . То есть радиус лежит в пределах
. То есть радиус лежит в пределах 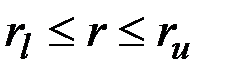 и,
и,
если 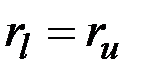 , то
, то 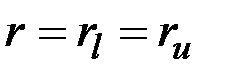 . (2.1)
. (2.1)
Таким образом, радиус графа и одну из его центральных вершин можно найти итеративным увеличением нижней границы радиуса rl и уменьшением его верхней границы ru до тех пор, пока не будет выполнено равенство 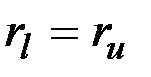 .
.
Для быстрого поиска радиуса необходимо находить вершины-претенденты на центр 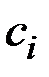 с как можно большей нижней границей rl
с как можно большей нижней границей rl
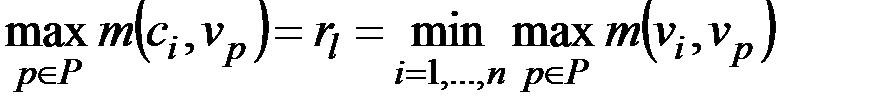 (2.2)
(2.2)
и с как можно меньшим эксцентриситетом 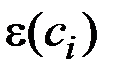 . При этом желательно, чтобы число просмотренных претендентов на центр ci и вершин в P было невелико, это позволит существенно уменьшить число решений задачи о кратчайших путях с единственным источником (Single Source Shortest Paths, SSSP, задача, в которой задан граф G=(V,Х), и необходимо найти кратчайшие пути от заданной вершины
. При этом желательно, чтобы число просмотренных претендентов на центр ci и вершин в P было невелико, это позволит существенно уменьшить число решений задачи о кратчайших путях с единственным источником (Single Source Shortest Paths, SSSP, задача, в которой задан граф G=(V,Х), и необходимо найти кратчайшие пути от заданной вершины 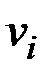 до всех остальных
до всех остальных 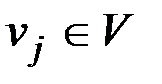 , примером такого алгоритма служит алгоритм фронта волны, разобранный в параграфе 2.7.2; поиск кратчайших расстояний от вершины
, примером такого алгоритма служит алгоритм фронта волны, разобранный в параграфе 2.7.2; поиск кратчайших расстояний от вершины 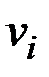 до всех остальных будем обозначать SSSP(
до всех остальных будем обозначать SSSP( 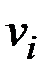 )). при решении задачи 1 и число просмотренных элементов матрицы минимальных расстояний М при решении задачи 2.
)). при решении задачи 1 и число просмотренных элементов матрицы минимальных расстояний М при решении задачи 2.
С этой целью в графе ищутся самые удаленные друг от друга вершины p1 и p2:  .
.
Для этого выбирается любая вершина графа d1, а вершина d2, определяется как самая удаленная от d1, т. е. 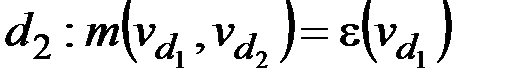 . Последующие вершины в данной «последовательности» определяются аналогичным образом
. Последующие вершины в данной «последовательности» определяются аналогичным образом
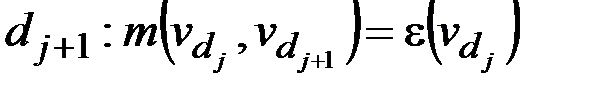 , j=2, 3, … (2.3)
, j=2, 3, … (2.3)
Процесс продолжается до тех пор, пока не будет выполнено равенство
 . (2.4)
. (2.4)
В этом случае искомые вершины найдены:
 . (2.5)
. (2.5)
Найденные вершины p1 и p2 включаются в пустое до этого множество опорных вершин P={p1,p2}. Претенденты на центр ci определяются по формуле (2.2). Если для первого претендента на центр c1 выполняется равенство rl=ru, данная вершина является одним из центров графа и радиус графа r=rl=ru. Если же  , самая удаленная от c1 вершина
, самая удаленная от c1 вершина 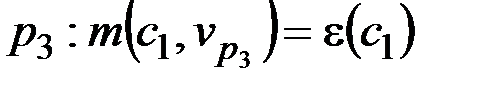 добавляется во множество опорных вершин P и выполняется поиск c2 по формуле (2.2). Общая формула поиска следующей опорной вершины
добавляется во множество опорных вершин P и выполняется поиск c2 по формуле (2.2). Общая формула поиска следующей опорной вершины
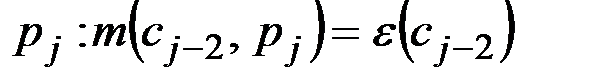 . (2.6)
. (2.6)
Процесс продолжается до тех пор, пока для какого-то из претендентов не будет выполнено равенство (2.1).
Следует отметить, что количество опорных вершин ограничено количеством вершин графа, т. е. точное решение получается с помощью конечного количества итераций. Теоретически оценить необходимое количество итераций затруднительно (как в методе ветвей и границ, подглава 2.7), но на реальных примерах в [9] показано, что достигается значительное ускорение процесса по сравнению с известными алгоритмами.
Ниже представлено описание алгоритма поиска радиуса и центральной вершины графа для задачи 1. Предложенный алгоритм также применим к задаче 2, с тем лишь отличием, что в случае задачи 2 для вершин не нужно решать задачу SSSP, так как уже известны расстояния между всеми парами вершин в виде матрицы M.
Алгоритм поиска центра и радиуса (Р)
Вход: граф G=(V,Х,U)
Выход: центральная вершина и радиус графа
0. Подготовка
rl=0, ru=∞
1. Построение исходного опорного множества
d1 – любая вершина графа
Определяем d2 по (2.3)
До тех пор пока не выполняется равенство (2.4)
Определяем d i по (2.3)
Определяем p1, p2 по (2.5). P ={p1, p2}
При этом для каждой di предварительно решаем SSSP(di)
2. Выбор претендента на центр
Определяем ci и rl по (2.2)
3. Проверка претендента
Если SSSP(ci) не решена, решаем SSSP(ci)
Находим 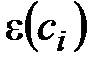 .
. 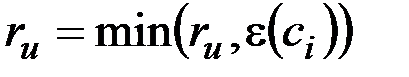
Если ru ≠ rl
Определяем p j по (2.6)
Если SSSP(pj) не решена, решаем SSSP(pj)
P = P + {pj}, переходим к шагу 2
Иначе c = ci , r = rl, конец алгоритма.
Результат: c– один из центров графа, r – радиус графа.
Метод и алгоритм поиска диаметра транспортной сети
При поиске радиуса хорошим приближением центральной вершины считалась вершина, минимально удаленная от периферийных вершин графа – т. е. та, которая находится «в центре» самых удаленных друг от друга вершин графа. Из-за высокой вычислительной сложности нахождения периферийных вершин графа в алгоритме поиска радиуса вместо них использовалось некоторое к ним приближение – множество опорных вершин P.
При поиске диаметра графа можно сделать обратное предположение – считать, что хорошим приближением периферийных вершин являются вершины, часть которых максимально удалена от центра графа. Имея вычисленную по алгоритму Р центральную вершину c и некоторую нижнюю оценку диаметра графа dl (равную, например, максимальному из уже найденных эксцентриситетов вершин) можно проверять на периферийность только пары вершин (vi, vj), расстояние до хотя бы одной из которых от центра больше dl/2:
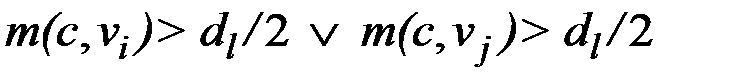 .
.
Использование в неравенствах в качестве точки отсчета центральной вершины вместо произвольной имеет выгодное отличие. В большинстве случаев просматривается меньшее число «мнимых» периферийных вершин vi – вершин с расстоянием удовлетворяющим m(c,vi) > dl/2, но не являющихся периферийными. Рис. 2.41 и 2.42 иллюстрируют это отличие наглядно.
Для графов большой размерности проверка вершин-претендентов на периферийные может занять много времени. Пусть граф содержит 107 вершин, 106 из которых являются претендентами на периферийные. Тогда в худшем случае для определения диаметра просто просмотреть потребуется больше ((106)2–106)/2≈5∙1011 пар вершин, причем расстояния между вершинами многих из этих пар будет гораздо меньше диаметра графа.
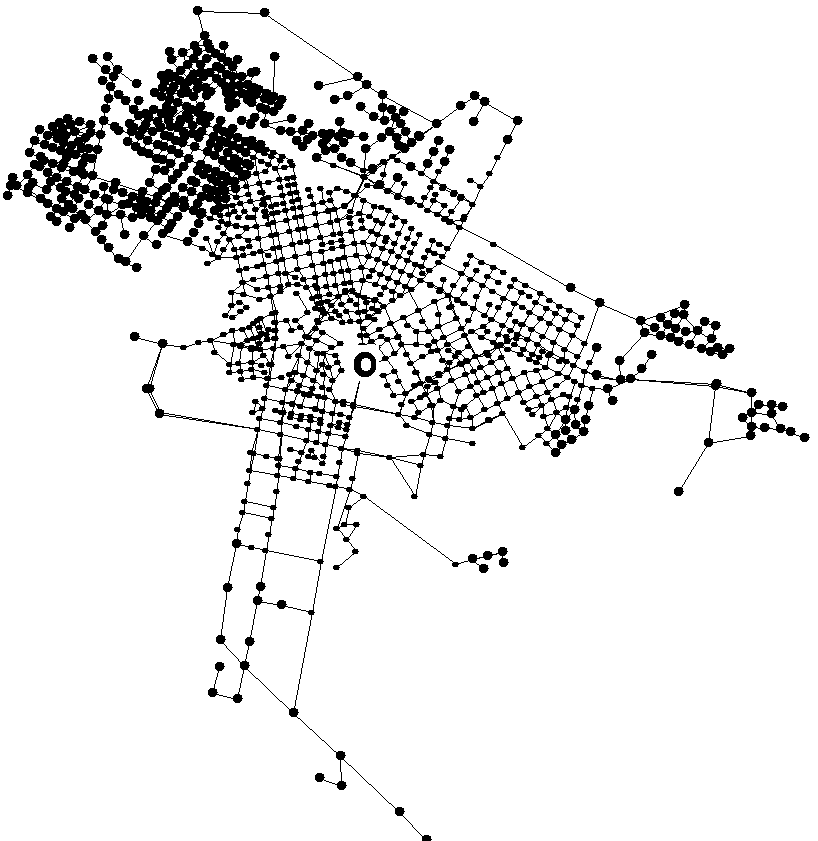
Рис. 2.41. Претенденты на периферийные вершины vi (помечены жирными точками) с расстоянием mc,vi) > dl/2 при выборе в качестве c центральной вершины графа (помечена кругом). Общее количество – 516

Рис. 2.42. Претенденты на периферийные вершины vi (помечены жирными точками) с m(c,vi) > dl/2 при выборе в качестве c вершины ближе к «краю» графа (помечена кругом). Общее количество – 816
Рис. 2.43 демонстрирует граф с большим количеством претендентов на периферийные вершины (≈9,5∙105), проверка пар вершин, в которых обе вершины из одной группы (1, 2 или 3), не имеет особого смысла.
В этой связи необходимо изменять подход к поиску диаметра, в зависимости от количества вершин-претендентов, типа, плотности и других параметров графа. Если с учетом этих параметров сложность просмотра пар претендентов относительно невелика, можно ее выполнить. В противном случае требуется сократить число возможных пар (например, не рассматривая пары располагающихся рядом вершин) и только после выполнять их проверку. Ниже дается формальное описание алгоритма.
Алгоритм поиска диаметра состоит из двух частей:
1) находится одна из центральных вершин графа с использованием описанного выше алгоритма;
2) производится непосредственный поиск диаметра.
Из рассмотрения исключаются вершины, которые не могут быть периферийными, для этого используются соотношения, предложенные Тейксом и Костерсом [1]. После осуществляется ветвление алгоритма в зависимости от числа оставшихся вершин-претендентов. На основе информации о расстояниях от центральной вершины (или центральных вершин) до остальных вершин графа производится дальнейший поиск диаметра.
Таким образом, данный алгоритм может называться алгоритмом поиска радиуса и диаметра.
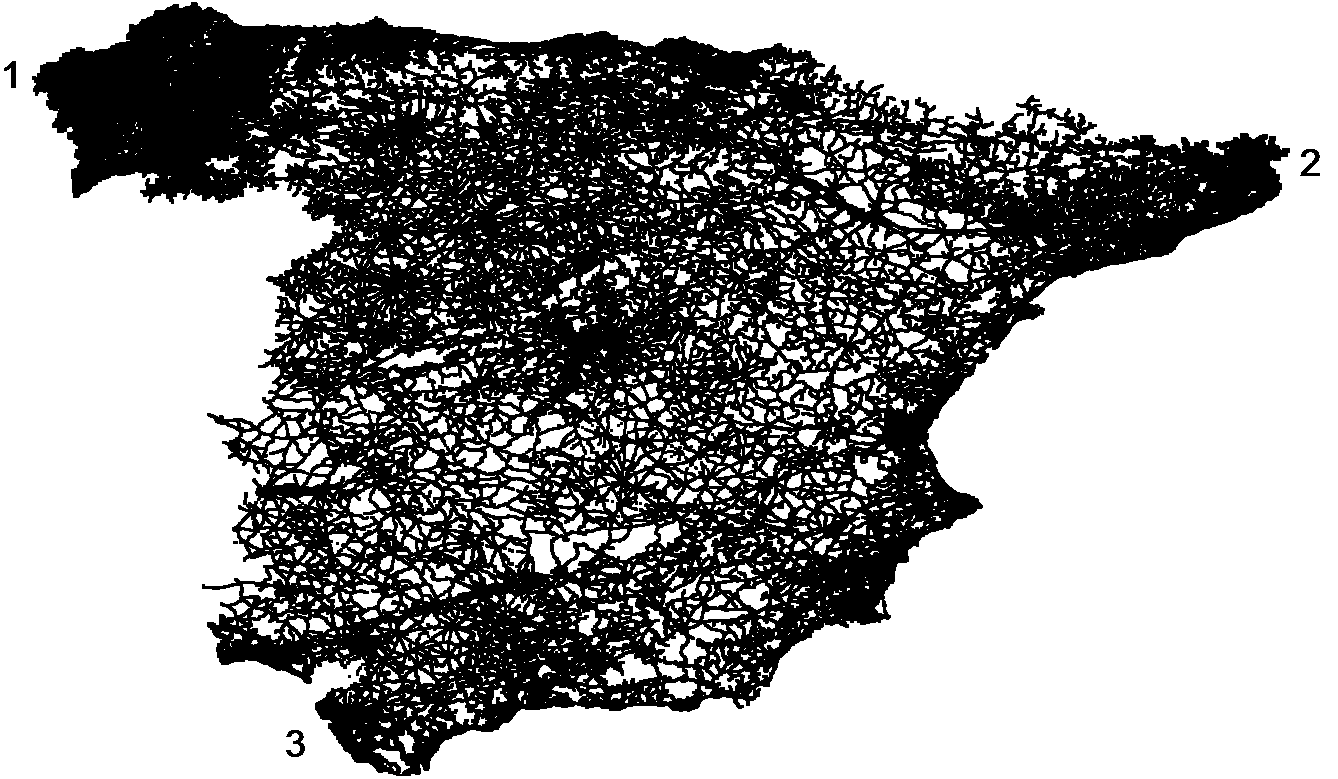
Рис. 2.43. Пример графа с большим количеством вершин – претендентов на периферийные. Цифрами обозначены три образованные претендентами группы
Первая часть алгоритма – поиск центральной вершины. Используя алгоритм Р (описан выше), находится одна из центральных вершин графа c. В процессе поиска c для некоторого множества вершин графа S={si} решается задача SSSP, т. е. для всех вершин этого множества известны кратчайшие расстояния, в том числе эксцентриситеты ε(si).
Начальные значения нижней и верхней границ диаметра полагаются равными: dl=0, du=∞. Используя вычисленные эксцентриситеты ε(si) вершин множества S, по формулам (2.7, 2.8) изменяются значения верхней и нижней границ. Верхняя оценка du – максимально возможное расстояние между парой вершин графа. По правилу треугольника кратчайшее расстояние между двумя произвольными вершинами графа не больше, чем длина пути между ними, проходящего через какую-либо вершину si, каждый из подпутей которого в свою очередь не больше эксцентриситета вершины si.
 , (2.7)
, (2.7)
 . (2.8)
. (2.8)
Далее производится сокращение числа вершин-претендентов на периферийные – по методу [1]. Во время работы алгоритма для каждой вершины vi хранятся значения нижней εl(vi) и верхней εu(vi) границ эксцентриситета. В начале для всех вершин они полагаются равными: 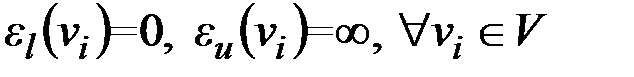 . Каждый эксцентриситет ε(si) вершин множества S позволяет уточнить значения этих границ по формулам (2.9), (2.10).
. Каждый эксцентриситет ε(si) вершин множества S позволяет уточнить значения этих границ по формулам (2.9), (2.10).
 , (2.9)
, (2.9)
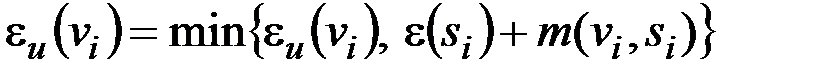 . (2.10)
. (2.10)
Из рассмотрения исключаются вершины vi, значения нижней и верхней границ эксцентриситета которых не входят в отрезок, ограниченный текущими оценками диаметра dl и du. Также исключаются из рассмотрения вершины с вычисленным эксцентриситетом – вершины, у которых нижняя и верхняя границы эксцентриситета равны. Формально правила исключения вершин описываются следующими формулами (согласно (2.7), (2.8))
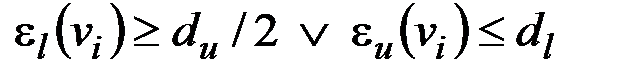 , (2.11)
, (2.11)
 . (2.12)
. (2.12)
После первоначального исключения вершин остается множество потенциально периферийных вершин 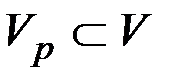 . С учетом мощности множества Vp, плотности, типа и других характеристик графа необходимо решить: выполнять ли попарную проверку оставшихся претендентов или предварительно сократить число возможных пар. Критерий выбора нужной ветви алгоритма, по сути, должен опираться на параметры, значения которых не известны заранее: число решений SSSP в каждой ветви алгоритма, общее число пар, которые необходимо просмотреть с учетом дальнейших исключений вершин, и т. д. В этой связи критерий выбора ветви алгоритма для каждого отдельного случая, по-видимому, должен формироваться эмпирически, на основе опыта, полученного при использовании алгоритма на достаточно большом количестве разного вида графов. При проведении экспериментов в [9] использовался критерий 5%: если число вершин в множестве Vp не больше 5% от общего числа вершин в графе – выполняем попарную проверку, иначе сокращаем число пар, которые необходимо проверить.
. С учетом мощности множества Vp, плотности, типа и других характеристик графа необходимо решить: выполнять ли попарную проверку оставшихся претендентов или предварительно сократить число возможных пар. Критерий выбора нужной ветви алгоритма, по сути, должен опираться на параметры, значения которых не известны заранее: число решений SSSP в каждой ветви алгоритма, общее число пар, которые необходимо просмотреть с учетом дальнейших исключений вершин, и т. д. В этой связи критерий выбора ветви алгоритма для каждого отдельного случая, по-видимому, должен формироваться эмпирически, на основе опыта, полученного при использовании алгоритма на достаточно большом количестве разного вида графов. При проведении экспериментов в [9] использовался критерий 5%: если число вершин в множестве Vp не больше 5% от общего числа вершин в графе – выполняем попарную проверку, иначе сокращаем число пар, которые необходимо проверить.
На рис. 2.44 показана блок-схема алгоритма поиска диаметра. Ниже описываются обе ветви алгоритма – попарная проверка вершин и сокращение числа пар проверяемых вершин.
Все упоминаемые в обеих ветвях алгоритма вершины vi, vj и т. п. подразумеваются принадлежащими множеству неисключенных вершин-претендентов Vp. Для эффективной работы алгоритма этот факт должен учитываться при конечной реализации в виде программы на выбранном языке программирования.
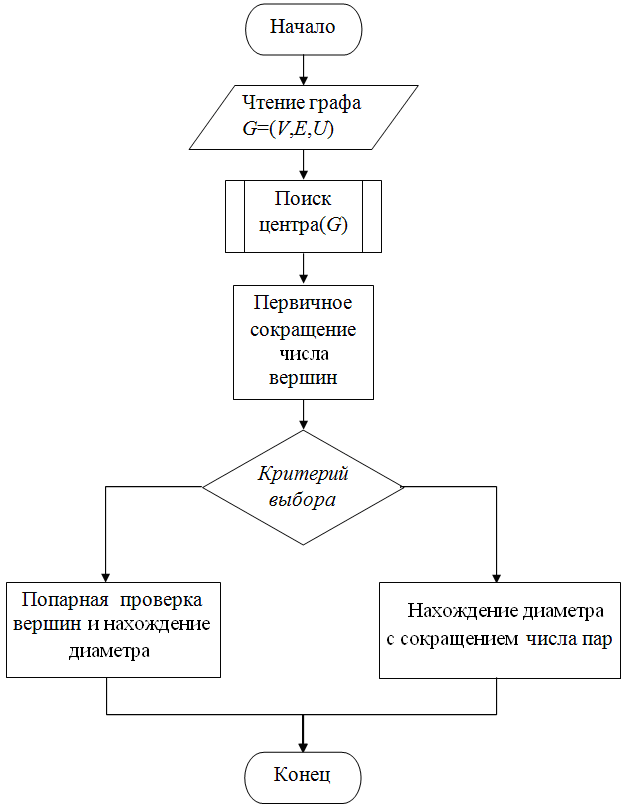
Рис. 2.44. Блок-схема алгоритма поиска диаметра графа.
Пороговое значение критерия выбора определяется эмпирически
По определению кратчайшего расстояния для расстояний между произвольными тремя вершинами vi, vj и vk справедливо неравенство треугольника
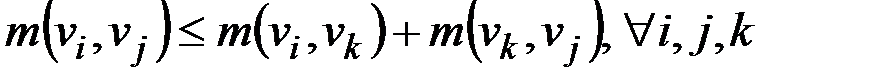 . (2.13)
. (2.13)
Значит, вычислив расстояния от некоторой вершины v q до всех остальных, для определения диаметра нужно просматривать расстояния только между теми парами вершин vk, vl, сумма расстояний которых до v q больше нижней границы dl. В качестве вершины v q в алгоритме используется найденная центральная вершина графа c, при которой это условие записывается в виде неравенства
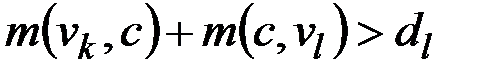 . (2.14)
. (2.14)
Согласно (2.13) потенциально наибольшим расстоянием между собой обладают вершины vk, vl с максимальной суммой 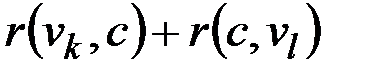 . Поэтому имеет смысл рассматривать вершины vk, vl в порядке убывания величины
. Поэтому имеет смысл рассматривать вершины vk, vl в порядке убывания величины  . Если при таком проходе «сверху вниз» для какой-то из пар вершин vk, vl неравенство (2.14) не выполняется, то просмотр остальных пар, обладающих меньшим потенциальным расстоянием между собой, не нужен.
. Если при таком проходе «сверху вниз» для какой-то из пар вершин vk, vl неравенство (2.14) не выполняется, то просмотр остальных пар, обладающих меньшим потенциальным расстоянием между собой, не нужен.
Для ускорения алгоритма вместо сортировки пар vk, vl по сумме  сортируются вершины vi по расстоянию до центра
сортируются вершины vi по расстоянию до центра 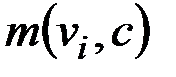 , а проверка по формуле (2.14) выполняется для пар вершин в порядке
, а проверка по формуле (2.14) выполняется для пар вершин в порядке
 (2.15)
(2.15)
Здесь mi – номер вершины с i-м по величине расстоянием до центра графа. Если для некоторых 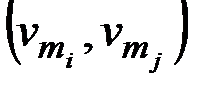 условие (2.14) не выполняется, переходим к просмотру
условие (2.14) не выполняется, переходим к просмотру  . Если (2.14) не выполняется и при этом j = i + 1, то поиск заканчивается и dl – диаметр графа. Поиск диаметра также останавливается, если текущие нижняя и верхняя границы диаметра равны: dl = d u.
. Если (2.14) не выполняется и при этом j = i + 1, то поиск заканчивается и dl – диаметр графа. Поиск диаметра также останавливается, если текущие нижняя и верхняя границы диаметра равны: dl = d u.
Проверка пары вершин 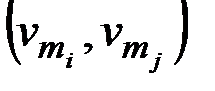 производится следующим образом. Сначала проверяется наличие пути между вершинами
производится следующим образом. Сначала проверяется наличие пути между вершинами  длиной diSj – формула (2.16) – не больше текущей нижней границы диаметра dl, проходящего через одну из вершин множества S с уже решенными задачами SSSP
длиной diSj – формула (2.16) – не больше текущей нижней границы диаметра dl, проходящего через одну из вершин множества S с уже решенными задачами SSSP
 . (2.16)
. (2.16)
Если такой путь существует, т. е.  , переходим к следующей паре в последовательности (2.15). В противном случае решаем задачу SSSP для любой из вершин пары, уточняем на основании полученной информации нижние и верхние границы диаметра и эксцентриситетов вершин по формулам (2.5–2.8) и производим дальнейшее исключение вершин, используя условия (2.9, 2.10). Ниже дано описание данной ветви алгоритма, для большей наглядности вычисление пары периферийных вершин опущено – они могут быть найдены как вершины, на которых во время работы алгоритма была достигнута наибольшая величина нижней границы dl.
, переходим к следующей паре в последовательности (2.15). В противном случае решаем задачу SSSP для любой из вершин пары, уточняем на основании полученной информации нижние и верхние границы диаметра и эксцентриситетов вершин по формулам (2.5–2.8) и производим дальнейшее исключение вершин, используя условия (2.9, 2.10). Ниже дано описание данной ветви алгоритма, для большей наглядности вычисление пары периферийных вершин опущено – они могут быть найдены как вершины, на которых во время работы алгоритма была достигнута наибольшая величина нижней границы dl.
Дата добавления: 2021-02-10; просмотров: 514; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
