Ветвь 1. Попарная проверка вершин и нахождение диаметра 9 страница
а б
Рис. 2.73. Пример сборки неориентированного нагруженного графа. Шаг 2;
а – граф G2; б – граф G1
1) Теперь добавляем вершину 
, смежные ей вершины 
(рис. 2.74) Пересчитываем значения весовых коэффициентов ребер, связывающих уже восстановленные вершины 
и 
:
;
;
;
;
.
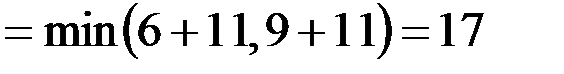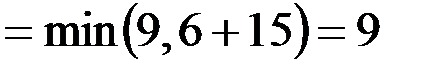Согласно найденным кратчайшим расстояниям элементы матрицы последователей в ячейках 
, 
, 
, 
, изменяются на 
, 
, 
– на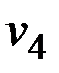 
. Элементы матрицы последователей в ячейках 
, 
, 
, 
не изменяются соответственно, так как были определены в начале алгоритма.
В матрицу кратчайших расстояний M в ячейки 
и 
заносится пересчитанное значение 
, в ячейки 
и 
– 
, в ячейки 
и 
– 
. 
и 
не меньше записанных в матрице М, поэтому значения в соответствующих ячейках не меняются.
В результате применения метода разборки-сборки графа получили матрицу кратчайших расстояний M и матрицу последователей P для минимальных путей.
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
а б
|
|
|
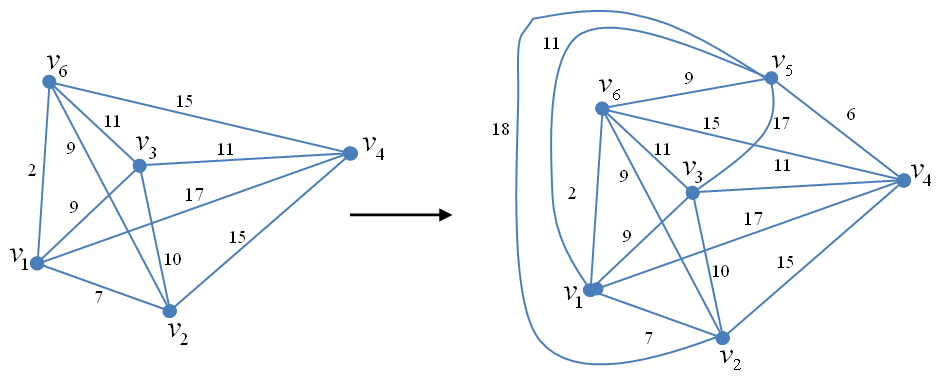
Рис. 2.74. Пример сборки неориентированного нагруженного графа. Шаг 1;
а – граф G1; б – граф G0
v Решение задачи для орграфа
0) Рассмотрим нагруженный орграф (рис. 2.75), который является односторонне связным.
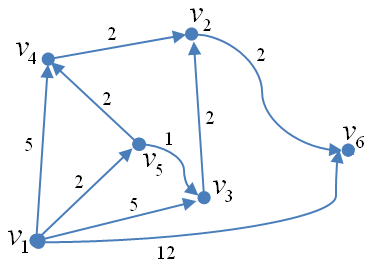
Рис. 2.75. Пример ориентированного нагруженного графа
Дана матрица его весов, необходимо найти минимальные пути между каждой парой вершин. На начальном этапе множество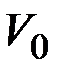 
содержит все вершины графа 
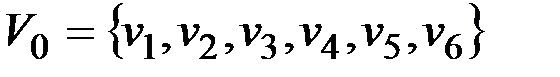. Вначале формируемая матрица кратчайших расстояний 
совпадает с матрицей длин дуг. Также вводится матрица последователей P, в которую заполняется информация о дугах.
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Разборка графа
1) На первом этапе так же, как и в предыдущем случае, выбираем вершину наименьшей степени: 
(ее степень 2). Имеем множества 
и 
. Поскольку из дуги 
путей нет, начальная матрица кратчайших расстояний 
и матрица последователей P не меняются. При этом получаем граф 
(рис. 2.76).
|
|
|
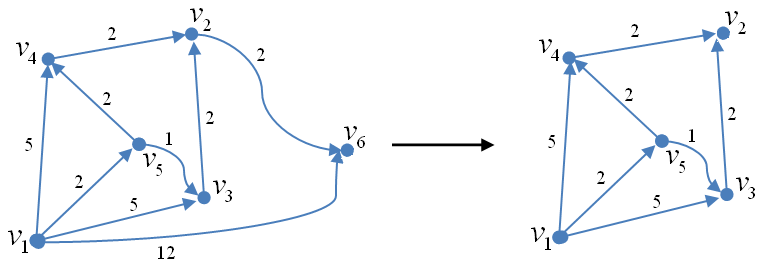
а б
Рис. 2.76. Пример разборки ориентированного нагруженного графа. Шаг 1;
а – граф G0; б – граф G1
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2) Удаляем следующую вершину наименьшей степени, теперь это 
, т. е. 
. Тогда множество 
и 
. Поскольку из дуги 
путей нет, матрицы 
и P не меняются
(рис. 2.77).
а б
Рис. 2.77. Пример разборки ориентированного нагруженного графа. Шаг 2;
а – граф G1; б – граф G2
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3) Удаляем следующую вершину наименьшей степени, 
. Тогда множество 
и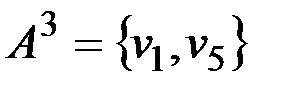 
. Матрицы 
и P не меняются. Получаем граф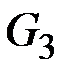 
(рис. 2.78).
а б
Рис. 2.78. Пример разборки ориентированного нагруженного графа. Шаг 3;
а – граф G2; б – граф G3
| Матрица последователей P | Матрица кратчайших расстояний M | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Дата добавления: 2021-02-10; просмотров: 73; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!