Ветвь 1. Попарная проверка вершин и нахождение диаметра 1 страница

⇐ ПредыдущаяСтр 2 из 15Следующая ⇒

Вход: граф G = (V, X, U), множества V_p, S,

центральная вершина c , d_l, d_u

Выход: диаметр графа, пара периферийных вершин

1. Сортировка пар

Пары вершин 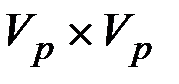сортируются в порядке (2.15)

i = 1, j = 1, ppOK = 0

2. Проверка пар

Для i от 1 до |V_p|–1

Для j от i+1 до |V_p|

Если 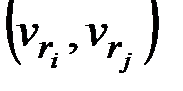удовлетворяют (2.14)

ppOK = 1

Вычисляем d_iSj по (2.16)

Если d_iSj > d_l

Решаем SSSP( )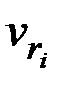

Вычисляем d_l, d_u по (2.7, 2.8)

Если d_l = d_u, d = d_l, конец алгоритма

Иначе отсекаем вершины по (2.9–2.12)

Иначе

Если ppOK = 0, d = d_l, конец алгоритма

Иначе ppOK = 0, конец цикла по j.

Конец цикла по j

Конец цикла по i

Результат: d – диаметр графа.

Основная идея этой ветви алгоритма заключается в уменьшении числа пар вершин-претендентов, которые необходимо просмотреть для нахождения диаметра, отсечением пар заведомо находящихся на меньшем друг от друга расстоянии, чем текущая нижняя граница диаметра. Для определения отсекаемых пар используется информации о расстояниях от небольшого числа вершин, определяемых по ходу данной ветви алгоритма.

После первоначального исключения вершин с использованием формул (2.7–2.12) граф приобретает вид, изображенный на рис. 2.43. Множества вершин, отмеченные цифрами, составляют неисключенные вершины V_p. Один из очевидных способов уменьшения числа рассматриваемых пар – не рассматривать пары, в которых обе вершины лежат близко друг к другу. На рис. 2.43 близко лежащие вершины образуют три явно выделяемых группы или кластера, обозначенные цифрами 1, 2 и 3. То есть для определения степени близости неисключенных вершин можно использовать кластеризацию вершин V_p на основании расстояний до некоторых опорных вершин.

Первые две опорные вершины p_d₁, p_d₂ определяются как элементы множества вершин с решенной задачей SSSP S, соединяемые путем максимальной длины

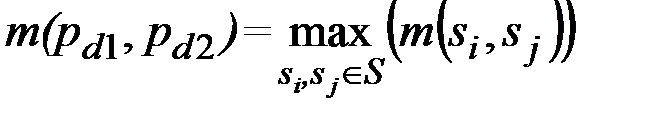. (2.17)

Каждая следующая опорная вершина p_di определяется как вершина v_j, чье минимальное удаление 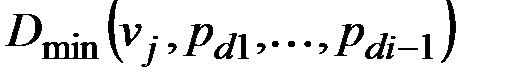(2.18) от уже найденных опорных вершин 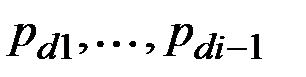максимально (2.19). Поиск опорных вершин продолжается до тех пор, пока существует вершина v_j, для минимального удаления которой справедливо неравенство .

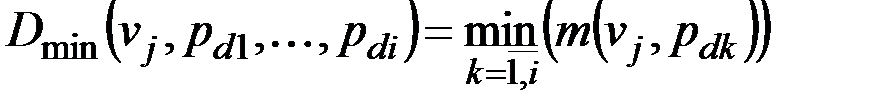, (2.18)

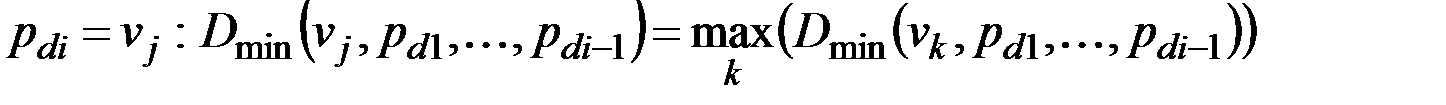. (2.19)

После нахождения всех опорных вершин создается t множеств-кластеров C₁,C₂,…,C_t – по числу найденных опорных вершин. Первыми в кластеры добавляются найденные опорные вершины: C₁ = {p_d₁},…,C_t = {p_dt}. Каждая из оставшихся вершин v_j множества V_p присоединяется к тому кластеру, чья опорная вершина находится к v_j ближе, чем опорные вершины остальных кластеров – формула (2.20). В случае нескольких опорных вершин с минимальным до v_j расстоянием, вершину можно присоединить к любому из кластеров этих опорных вершин.

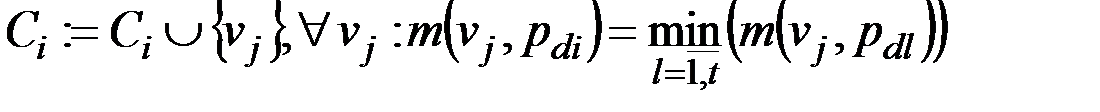. (2.20)

После кластеризации всех вершин множества V_p можно рассматривать лишь пары, образованные вершинами из разных кластеров 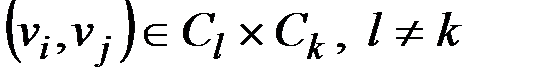. Это позволяет значительно сократить число просматриваемых пар вершин, однако может быть не достаточным, если после кластеризации образуются два и более кластера большой мощности. Можно дополнительно уменьшить число просматриваемых пар, используя центры полученных кластеров.

Пусть у каждого кластера C_i вычислен центр c_i. Тогда любую рассматриваемую пару кластеров C_i и C_j можно разбить, как схематически показано на рис. 2.45.

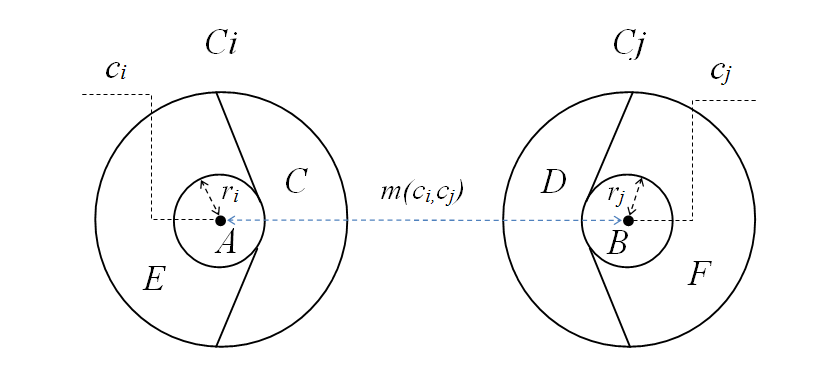
Рис. 2.45. Схематическое изображение разбиения кластеров вершин C_i и C_j

на 8 непересекающихся множеств. c_i и c_j – центральные вершины кластеров

Каждый кластер разбит на четыре подмножества. Например, кластер C_i разбит на:

1) c_i – центральная вершина кластера;

2) A – r_i-окрестность центра кластера c_i – вершины v_i кластера C_i, для которых справедливо

; (2.21)

3) C – вершины v_i кластера C_i, расстояние между которыми и центром c_j кластера C_j не больше расстояния между вершинами множества A и c _j

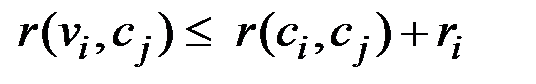; (2.22)

4) E – вершины кластера C_i не вошедшие ни в одно из этих множеств

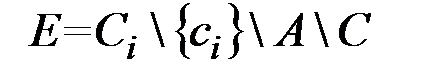. (2.23)

Аналогичным образом определяется разбиение на подмножества кластера C_j. При таком разбиении кластеров и заданных величинах r_i и r_j, отвечающих равенству

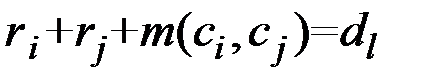, (2.24)

необходимо проверять на периферийность лишь пары вершин, образованные декартовыми произведениями множеств

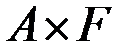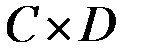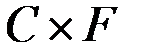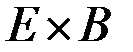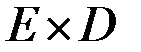, , , , , . (2.25)

Действительно, расстояние между вершинами пар произведения не больше нижней границы диаметра в силу (2.21) и (2.24). Расстояние между парами вершин 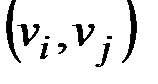произведени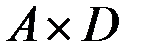й и 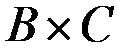также не больше нижней границы диаметра: по (2.22) имеем для :

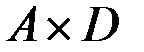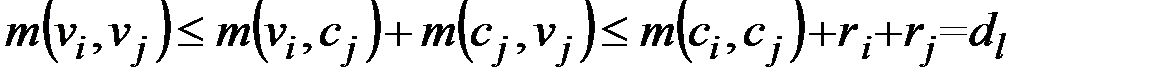Аналогично для произведения .

Для ускорения решения необходимо подобрать параметры r_i, r_j при известных расстояниях для каждой пары кластеров C_i, C_j так, чтобы минимизировать общее количество пар сравнения:

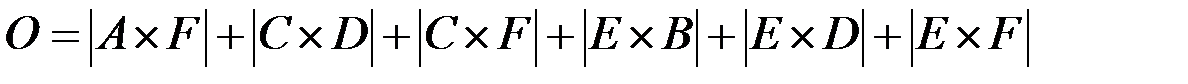. (2.26)

Поиск минимума (2.26) выполняется следующим образом. Интервал изменения 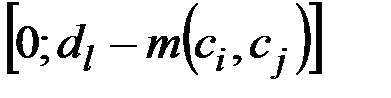параметров r_i, r_j разбивается на k частей: 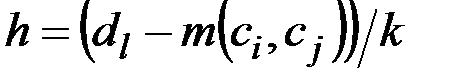. На первой итерации поиска величины параметров полагаются равными , . После этого вычисляется значение O из формулы (2.26). На каждой итерации l параметрам присваиваются значения 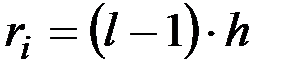, и вычисляется значение O. По окончании k+1 итерации поиска выбирается разбиение кластеров C_i, C_j с такими параметрами r_i, r_j, при которых было зафиксировано минимальное значение O. Ниже приводится описание данной ветви алгоритма, проверка пар вершин осуществляется схожим с приведенным для ветви 1 алгоритма образом.

Ветвь 2. Нахождение диаметра с сокращением числа пар

Вход: граф G = (V, X, U), множества V_p, S,

d_l, d_u

Выход: диаметр графа, пара периферийных вершин

1. Кластеризация вершин

Вычисляются опорные вершины кластеров по формулам (2.17–2.19)

Все остальные вершины V_p кластеризуются по C_i с использованием (2.20)

Вычисляются центры c_i всех кластеров C_i

2. Попарная проверка кластеров

Для каждой пары C_i, C_j: j > i

Вычисляются r_i, r_j, удовлетворяющие (2.24), с минимумом (2.26)

Производится разбиение каждого кластера по (2.21–2.23)

Выполняется проверка пар вершин произведений (2.25)

Пример

v Задача 1

Рассмотрим неориентированный нагруженный граф и найдем его метрические характеристики (рис. 2.46).

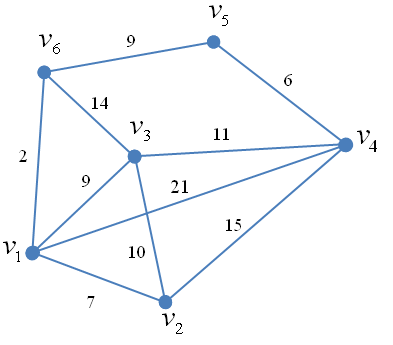
Рис. 2.46. Пример неориентированного нагруженного графа

Представим данный нагруженный граф в виде матрицы длин ребер. Необходимо найти радиус, центр и диаметр графа.

	v₁	v₂	v₃	v₄	v₅	v₆
v₁	0	7	9	21	∞	2
v₂	7	0	10	15	∞	∞
v₃	9	10	0	11	∞	14
v₄	21	15	11	0	6	∞
v₅	∞	∞	∞	6	0	9
v₆	2	∞	14	∞	9	0

Сначала найдем радиус и один из центров графа, используя алгоритм Р. Зададим начальные значения нижней и верхней границ радиуса: r_l = 0, r_u = ∞. Далее определяем две первые вершины опорного множества P. Предположим, что в качестве d₁ была выбрана вершина v₁. Так как нам не известны кратчайшие расстояния от v₁ до остальных вершин графа, решаем задачу SSSP(v₁).

В результате получим видоизмененную матрицу длин ребер, где 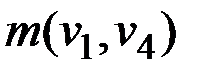= = 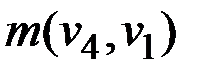21 заменяется на меньшее 17, = заменяется на 11.

Определяем d₂ по формуле (2.4), как самую удаленную вершину от d₁ = v₁. В данном случае самой удаленной оказывается вершина v₄ с кратчайшим расстоянием до v₁ равным 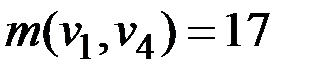, полагаем d₂ = v₄.

	v₁	v₂	v₃	v₄	v₅	v₆
v₁	0	7	9	17	11	2
v₂	7	0	10	15	∞	∞
v₃	9	10	0	11	∞	14
v₄	17	15	11	0	6	∞
v₅	11	∞	∞	6	0	9
v₆	2	∞	14	∞	9	0

Для v₄ кратчайшие расстояния не вычислены, поэтому решаем SSSP(v₄), получая следующие изменения в матрице длин ребер: = заменяется на меньшее 15.

Находим вершину d₃, определяемую как самую удаленную от d₂. Ей является вершина v₁ с кратчайшим расстоянием равным 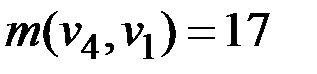, полагаем d₃ = v₁. Так как справедливо равенство 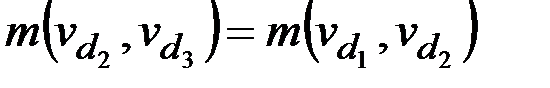– т. е. найдены две максимально удаленные друг от друга вершины – пополняем пустое до этого множество опорных вершин .

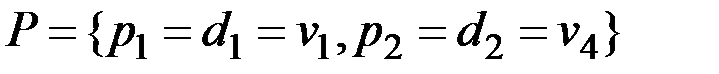	v₁	v₂	v₃	v₄	v₅	v₆
v₁	0	7	9	17	11	2
v₂	7	0	10	15	∞	∞
v₃	9	10	0	11	∞	14
v₄	17	15	11	0	6	15
v₅	11	∞	∞	6	0	9
v₆	2	∞	14	15	9	0

Далее выполняется проверка претендентов на центральную вершину с использованием информации о расстояниях от вершин опорного множества P. По формуле (2.2) находим первого претендента на центральную вершину c₁ – вершину, максимальное расстояние от которой до вершин множества P минимально среди всех остальных вершин. Таких вершин оказывается две:

1) v₃ с ;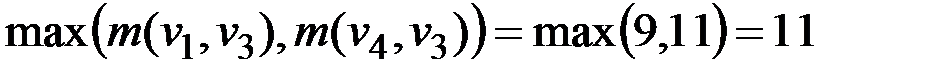

2) v₅ с .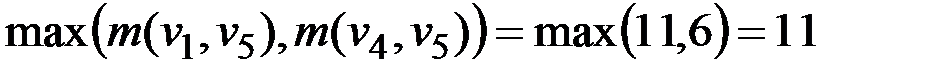

Выбираем любую из этих вершин, например, v₃, полагая c₁ = v₃. Соответствующим образом изменяем нижнюю границу радиуса r_l = 11.

Выполняем проверку претендента c₁. Для претендента кратчайшие расстояния не найдены, потому решаем SSSP(c₁ = v₃), матрица длин ребер после этого принимает следующий вид.

	v₁	v₂	v₃	v₄	v₅	v₆
v₁	0	7	9	17	11	2
v₂	7	0	10	15	∞	∞
v₃	9	10	0	11	17	11
v₄	17	15	11	0	6	15
v₅	11	∞	17	6	0	9
v₆	2	∞	11	15	9	0

Дата добавления: 2021-02-10; просмотров: 88; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!