Ветвь 1. Попарная проверка вершин и нахождение диаметра 3 страница

⇐ ПредыдущаяСтр 4 из 15Следующая ⇒

Наконец, рассматриваем вершину v₆. Значение нижней границы диаметра не изменяется: d_l = max(d_l, ε(v₆)) = (18, 15) = 18, верхняя граница уменьшается: d_u = min(d_u, 2∙ε(v₅)) = (34, 30) = 30. Уточняем нижнюю и верхнюю границы эксцентриситета вершины v₆:

ε_l(v₆) = max(ε_l(v₆), ε(v₆) – ,

) = max(15, 15 – 15, 15) = 15;

ε_u(v₆) = min(ε_u(v₆), ε(v₆) + 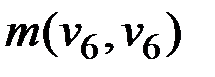) = min(19, 15 + 0) = 15.

Вершина v₆ исключается из рассмотрения, так как ε_l(v₆) = ε_u(v₆).

	v₁	v₂	v₃	v₄	v₅	v₆
ε_l	17	18	17	17	17	15
ε_u	17	24	17	34	28	15

Таким образом, из рассмотрения исключены все вершины и найден диаметр графа d = d_l = 18 и две периферийные вершины – v₂ и v₅(запомненные при нахождении эксцентриситета наибольшей величины ε(v₅)). В данном примере дальнейших ход алгоритма с попарной проверкой вершин оказался не нужным.

2.7.4 Уменьшение размерности графа транспортной сети

Рассматривается задача аппроксимации нагруженного графа большой размерности графом меньшей размерности с целевой функцией на минимум максимума разностей расстояний между вершинами исходного графа и соответствующими им вершинами полученного малого графа. Исследуются два варианта задачи, приводятся их формулировки в терминах задачи аппроксимации и задачи разбиения графа.

Рассматривается простой связный неориентированный нагруженный граф G = (V, X, U), где мощность множества вершин |V| = n.

Рассматриваемые задачи аппроксимации состоят в сопоставлении исходному графу G аппроксимирующего графа G_a = (V_a, X_a, U_a) меньшей размерности: |V_a| = n_a, где .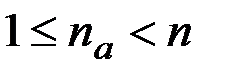

Будем называть вершины аппроксимирующего графа метавершинами и обозначать .

Метавершины могут быть подмножеством исходного множества вершин или не содержаться в V (как частично, так и полностью). Вес ребра между метавершинами и 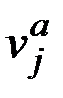графа G_a будем обозначать , расстояние между этими же метавершинами 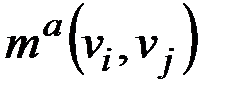. Будем обозначать 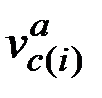метавершину графа G_a, аппроксимирующую вершину v_i графа G.

Погрешностью аппроксимации будем называть величину

. (2.27)

Рассмотрим две задачи аппроксимации:

1) уменьшение размерности G_a так, чтобы погрешность A_e не превосходила заданной величины;

2) уменьшение погрешности A_e при заданной размерности G_a.

Задача 1. Дан простой связный неориентированный нагруженный граф G = (V, X, U) с неотрицательной вещественной весовой функцией на ребрах и вещественное число e_max > 0. Найти граф G_a = (V_a, X_a, U_a) и функцию такие, что подграфы G_j(V_j): связны, и .

Задача 2. Дан простой связный неориентированный нагруженный граф G = (V, X, U): |V| = n с неотрицательной вещественной весовой функцией на ребрах U: X → [0, ∞) и целое число k: n > k > 0.

Найти граф G_a = (V_a, X_a, U_a): |V_a| = k и функцию соответствия

такие, что подграфы связны и A_e→ min.

Обе рассматриваемые задачи являются NP -трудными (см. Прил. 1). Эти задачи при некоторых допущениях могут быть сформулированы в терминах задачи разбиения графа. Введем обозначения, аналогичные рассмотренным выше: диаметр множества вершин , радиус множества вершин . Вершину, на которой достигается r(V_i), будем называть центром множества вершин V_i и обозначать c(V_i).

Будем аппроксимировать вершины подмножеств разбиения V_i центрами этих подмножеств 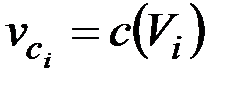. Веса ребер в графе G_a между этими центрами будем полагать равными расстояниям между центрами в исходном графе G: . Дополнительно будем требовать связность всех подграфов разбиения G_i(V_i).

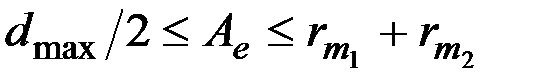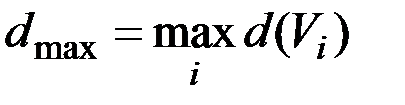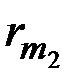При выполнении всех этих условий для погрешности аппроксимации справедливо . Здесь , – максимальный, а – второй по величине радиусы множеств разбиения V_i. Действительно, в этом случае погрешность аппроксимации внутри подграфов не превосходит
d_max/2 ≤ , а погрешность аппроксимации между вершинами v_i и v_j из разных подграфов не превосходит суммы расстояний от этих вершин до центров соответствующих подграфов, т. е. .

При такой оценке для A_e задачи разбиения графа, соответствующие поставленным задачам аппроксимации, выглядят следующим образом.

Задача 1*. Дан простой связный неориентированный нагруженный граф G = (V, X, U) с неотрицательной вещественной весовой функцией на ребрах и вещественное число e_max > 0. Найти разбиение множества вершин графа на попарно непересекающиеся подмножества {V₁,V₂,...,V_k}: , такое, что все подграфы G_i(V_i), порожденные этими множествами, связны, и k→ min.

Задача 2*. Дан простой связный неориентированный нагруженный граф G = (V, X, U):|V| = n с неотрицательной вещественной весовой функцией на ребрах и целое число k: n > k > 0. Найти разбиение множества вершин графа на k попарно непересекающихся подмножеств {V₁,V₂,...,V_k}: , такое, что все подграфы G_i(V_i), порожденные этими множествами, связны и .

Алгоритм для задачи 1 (A1)

Предлагаемый эвристический алгоритм состоит в последовательном «удалении» вершин графа. В процессе удаляемым вершинам в качестве метавершины в соответствие ставится одна из смежных вершин и выполняется пересчет весов ребер получившегося графа меньшей размерности.

Пусть на возможность удаления первой рассматривается вершина v_i степени m смежная с вершинами . Удаление v_i влечет необходимость изменения весов ребер только между смежными с ней вершинами . Пересчет весов данных ребер будем производить по формуле

После такого пересчета погрешность аппроксимации между всеми неудаленными вершинами останется равной нулю. Поэтому для минимизации общей погрешности аппроксимации необходимо поставить в соответствие удаленной вершине v_i такую метавершину v_c_(i), которая сделает как можно меньшим максимум абсолютной разности расстояний между v_i, v_c_(i) и вершинами исходного графа: . В исходном графе расстояния от v_i до любой вершины графа v_j определялись формулой . После удаления v_i расстояния между неудаленными вершинами 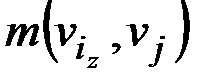не изменились.
В качестве v_c_(i) будем выбирать ближайшую смежную с v_i вершину 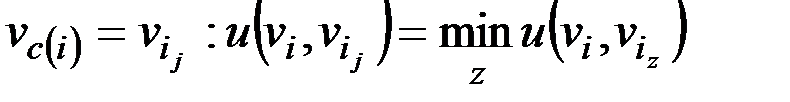, при этом погрешность аппроксимации увеличится не более чем на вес ребра .

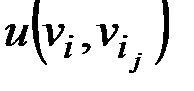В задаче 1 требуется, чтобы погрешность аппроксимации не превосходила некоторого заданного числа . Для достижения этого необходимо хранить информацию о погрешности , вносимой каждой из оставшихся вершин v_l. – максимально возможная погрешность аппроксимации между вершинами, аппроксимируемыми вершиной v_l (вначале все ). Удаление вершины v_i изменяет погрешность аппроксимирующей ее вершины v_c_(i) по правилу . В силу сохранения расстояний между оставшимися вершинами, для выполнения необходимо, чтобы для всех пар оставшихся вершин (v_l,v_j) выполнялось , а это справедливо, если . Согласно этому, вершину v_i можно удалять, когда для аппроксимирующей ее вершины v_c_(i) выполняется

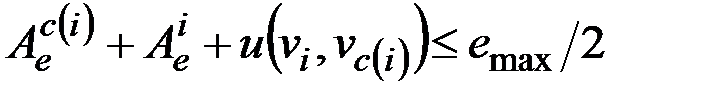(2.28)

Рассмотрение и удаление вершин может производиться различными способами. Одной из очевидных стратегий является удаление вершин в порядке роста добавляемой этими вершинами погрешности. Результаты тестирования алгоритма в [9] приводятся для случая, когда рассмотрение вершин происходит по мере роста их степеней. Такая стратегия показала наилучшие результаты на тестовых графах.

Полученная таким образом аппроксимация не гарантирует связности подграфов исходного графа, вершины которых аппроксимируются одной метавершиной. Используя следующее правило переопределения функции c, можно гарантировать связность таких подграфов, не увеличив при этом погрешность аппроксимации.

Пусть для всех множеств V_j найдены радиусы r(V_j) и центры c(V_j) (данные величины можно найти, используя алгоритмы быстрого поиска метрических характеристик из параграфа 2.7.3). Если для вершины 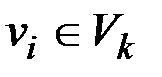отсутствует путь до центра c(V_k) в графе G_k(V_k), то в пути от v_i до c(V_k) в исходном графе G существует вершина .
В случае, если принадлежность вершины v_i множеству V_l не увеличивает r(V_l) и у вершины v_i принадлежность множеству не изменялась, полагаем c(i) = l. В противном случае все вершины v_s пути от v_i до v_j в исходном графе G делаем принадлежащими множеству V_k, полагая c(s) = k. После каждого изменения принадлежности множеству какой-либо из вершин центры и радиусы изменившихся множеств V_k, V_l пересчитывается и процесс повторяется снова, до тех пор, пока не останется несвязных подграфов. После полагаем w(c(V_j), c(V_j)) = r(V_j), c(i) = c(V_j), .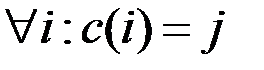

В худшем случае, когда для полного графа выполняется «удаление» n − 2 вершин, сложность алгоритма составляет O(n³).

Алгоритм для задачи 2 (A2)

Для решения задачи 2 предлагается итерационный алгоритм, в основе которого лежит алгоритм из предыдущего параграфа (A 1). Итеративно ищется такое значение величины e_max (и аппроксимация при этом значении), при котором решение задачи 1 алгоритмом A 1 позволит получить аппроксимирующий граф с числом вершин 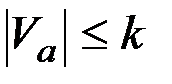, где k – ограничение из задачи 2.

Для поиска такого e_max используется предположение о зависимости 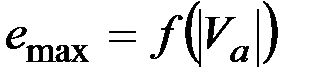и метод последовательных приближений, состоящий в следующем. Задаются нижняя e_l и верхняя e_u границы допуска e_max для задачи 1. Примем нижнюю границу e_l = 0, исходя из того, что граф с погрешностью аппроксимации A_e = 0 обладает тем же числом вершин, что и исходный граф. Верхняя граница e_u задается формулой , где q(v_i) – ребро максимального веса вершины v_i, так как при таком выборе допуска e_max аппроксимирующий граф будет состоять из одной вершины. Далее на каждой итерации ищется решение задачи 1 при допуске e_max = (e_l + e_u)/2. Если число вершин аппроксимирующего графа при данном допуске больше искомого |V_a| > k, изменяем верхнюю границу e_u = (e_l + e_u)/2, если же |V_a| < k, изменяем нижнюю границу e_l = (e_l + e_u)/2. На практике нахождение решения задачи с |V_a| = k, не всегда является возможным, поэтому поиск решения останавливается при |V_a| = k – D. В [9] использовалось значение D = 0,02×k.

Пример решения задачи аппроксимации

v Рассмотрим задачу 1 аппроксимации неориентированного нагруженного графа G (рис. 2.47). Требуется найти аппроксимирующий G граф G_a, минимизировав его порядок |V_a| → min, так чтобы погрешность аппроксимации A_e (2.27) не превосходила заданной величины A_e £ e_max. Зададим для данного примера e_max = 30.

Вершины будем рассматривать в порядке роста степеней. Если существует более одной вершин одинаковой степени, рассматриваем их по росту вносимой погрешности . Если среди них есть несколько с одинаковой вносимой погрешностью, рассматриваем вершины в порядке возрастания номера. На начальном этапе все значения .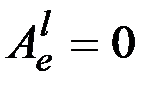

Рис. 2.47. Аппроксимируемый граф G

Первой рассматриваем вершину v₁(степень 3 является наименьшей). Это вершина может быть аппроксимирована v₃, так как (согласно (2.28)). Удаляем вершину v₁, пересчитываем веса ребер:

Дата добавления: 2021-02-10; просмотров: 75; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!