Определение плотности распределения

Выше непрерывная случайная величина задава­лась с помощью функции распределения. Этот способ задания не является единственным. Непрерывную слу­чайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют диф­ференциальной функцией).

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) — первую производную от функции распределения F(x):

f(x) = F'(x).

Из этого определения следует, что функция распре­деления является первообразной для плотности распре­деления.

Заметим, что для описания распределения вероятно­стей дискретной случайной величины плотность распре­деления неприменима.

Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме.

Теорема. Вероятность того, что непрерывная случай­ная величина X примет значение, принадлежащее интер­валу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

Геометрически полученный результат можно истолко­вать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограни­ченной осью Ох, кривой распределения f (х) и прямыми х = а и х = b.

 

Пример. Задана плотность вероятности случайной величины X

 

 

Найти вероятность того, что в результате испытания X примет зна­чение, принадлежащее интервалу (0,5; 1). Решение. Искомая вероятность

 

Нахождение функции распределения по известной плотности распределения

Зная плотность распределения f(x), можно найти функцию распределения F (х) по формуле

 

По известной функции распределения может быть найдена плотность распределения, а именно:

f(x) = F'(x).

Пример. Найти функцию распределения по данной плотности распределения:

Построить график найденной функции.

Решение. Воспользуемся формулой

Если х ≤ а, то f(x) = 0, следовательно, F (х) = 0. Если а < х ≤ b, то f(x) = 1/(b-a) следовательно,

Если х > b, то

Итак, искомая функция распределения

График этой функции изображен на рисунке

 

Свойства плотности распределения

Свойство 1.   Плотность распределения—не­отрицательная функция:

f(x)>0.

Геометрически это свойство означает, что точ­ки, принадлежащие графику плотности распреде­ления, расположены либо над осью Ох, либо на этой оси.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от —∞ до +∞ равен единице:

Геометрически это означает, что вся площадь криво­линейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (а, Ь), то

 

Числовые характеристики непрерывных случайных величин

Распространим определения числовых характе­ристик дискретных величин на величины непрерывные.

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл

Если возможные значения принадлежат всей оси Ох, то

По аналогии с дисперсией дискретной величины опре­деляется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [а, b], то

если возможные значения принадлежат всей оси х, то

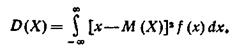
Среднее квадратическое отклонение непрерывной слу­чайной величины определяется, как и для величины диск­ретной, равенством

Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непре­рывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

Пример 1. Найти математическое ожидание и дисперсию случай­ной величины X, заданной функцией распределения

Решение. Найдем плотность распределения:

Найдем математическое ожидание

Найдем дисперсию

 

Контрольные вопросы.

1. Определение функции распределения. Пример
2. Свойства функции распределения.
3. График функции распределения. Пример
4. Что называют плотностью распределения вероятностей непрерывной случайной величины?
5. Как найти вероятность попадания непрерывной случайной величины в заданный интервал?
6. Свойства плотности распределения
7. Что называют математическим ожиданием непрерывной случайной величины?
8. Что называют дисперсией непрерывной случайной величины?
9. Как найти среднеквадратическое отклонение непрерывной случайной величины?
10. Может ли при каком-либо значении аргумента:

а) функция распределения быть больше 1?

б) плотность распределения вероятности быть больше 1?

в) функция распределения быть отрицательной?

г) плотность распределения вероятности быть отрицательной?

1. Почему f (x) носит название «плотность распределения вероятностей»?

 

 

Лекция № 7

Тема: «Нормальное распределение»

План лекции

1. Нормальное распределение. Нормальная кривая

2. Вероятность попадания в заданный интервал нормальной случайной величины

3. Вычисление вероятности заданного отклонения

4. Правило трех сигм

 

Нормальное распределение

Нормальным называют распределение вероятно­стей непрерывной случайной величины, которое описы­вается плотностью

Мы видим, что нормальное распределение определяется двумя параметрами: а и σ. Достаточно знать эти пара­метры, чтобы задать нормальное распределение.

Вероятностный смысл этих параметров таков: а есть математическое ожидание, σ — среднее квадратическое отклонение нормального распределения.

М (X) = а, т. е. математическое ожидание нор­мального распределения равно параметру а.

Среднее квадратическое отклонение нормального распределения равно параметру σ.

Нормальная кривая

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию методами дифференциального исчисления.

1. Очевидно, функция определена на всей оси х.

2. При всех значениях х функция принимает поло­жительные значения, т. е. нормальная кривая располо­жена над осью Ох.

3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: lim у = 0, т. е. ось Ох служит горизонтальной асимптотой графика.

На рисунке изображена нормальная кривая при а = 1 и σ = 2.

 

Вероятность попадания в заданный интервал нормальной случайной величины

Уже известно, что если случайная величина X задана плотностью распределения f(х), то вероятность того, что X примет значение, принадлежащее интервалу (α, β), такова:

Пусть случайная величина X распределена по нор­мальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу (α, β), равна

Преобразовывают эту формулу так, чтобы можно было пользоваться готовыми таблицами. Таким образом, имеем

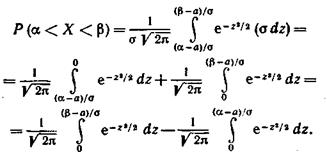 I

Пользуясь функцией Лапласа

окончательно получим

 

Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое откло­нение этой величины соответственно равны 30 и 10. Найти вероят­ность того, что X примет значение, принадлежащее интервалу (10, 50).

Решение. Воспользуемся полученной формулой

По условию, α =10, β = 50, а = 30, σ =10, следовательно

По таблице приложения 2 находим Ф (2) = 0,4772. Отсюда иско­мая вероятность

Р(10 < X < 50) = 2 - 0,4772 = 0,9544.

Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной вели­чины X по абсолютной величине меньше заданного по­ложительного числа δ, т. е. требуется найти вероятность осуществления неравенства

|Х—а|< δ.

Заменим это неравенство равносильным ему двойным неравенством

Пользуясь ранее полученной формулой, получим

Приняв во внимание равенство

 

Пример 1. Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение X соответственно равны 20 и 10. Найти вероятность того, что отклонение по абсолютной величине будет меньше трех.

Решение. Воспользуемся формулой

Р(|Х-а|< δ)=2Ф(δ / σ). По условию, δ = 3, а = 20, σ =10. Следовательно,

Р(|Х — 20 | < 3) = 2Ф (3/10) = 2Ф (0,3).

По таблице приложения 2 находим Ф (0,3) = 0,1179. Искомая вероятность

Р(|Х — 20| <3) = 0,2358.

 

Пример 2. Измерительный прибор (высотомер) имеет систематическую ошибку +20м и случайные ошибки Х, распределённые по нормальному закону с параметрами

M (X) = 0; σ = 10м. Определить: а) вероятность измерения высоты с ошибкой, не превышающей по абсолютной величине 50 м; б) какую точность измерения высоты можно гарантировать с вероятностью 0,98?

Решение. Пусть У – суммарная ошибка измерения высоты. Тогда У = 20+Х и М (У) = 20; D (У) = D (Х) = 100.

Таким образом,

Находим

а)

б)

 

Правило трех сигм

Преобразуем формулу

Р(|Х-а|< δ) = 2Ф(δ / σ) , положив δ = σ t. В итоге получим

Р(|Х— а|< σ t) = 2Ф(t).

Если t = 3 и, следовательно, σ t = Зσ, то

Р (| X — а |< Зσ) = 2Ф (3) = 2 ∙ 0,49865 = 0,9973,

т. е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

 

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципа невозмож­ности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математиче­ского ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выпол­няется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

 

Контрольные вопросы.

1. Что называют нормальным распределением?
2. Какими параметрами определяется нормальное распределение?
3. Чему равно математическое ожидание нормального распределения?
4. Чему равна дисперсия нормального распределения?
5. Почему f (x) носит название «плотность распределения вероятностей»?
6. Чему равно среднеквадратическое отклонение нормального распределения?
7. Какой график имеет нормальная кривая?
8. Как вычислить попадание в заданный интервал нормальной случайной величины?
9. Как вычислить вероятность заданного отклонения?
10. Как используется правило трех сигм?

 

Лекция № 8

Тема: «Статистическое распределение выборки. Эмпирическая функция распределения»

План лекции

1. Задачи математической статистики

2. Генеральная и выборочная совокупности

3. Статистическое распределение выборки

4. Эмпирическая функция распределения

5. Полигон и гистограмма

 

Задачи математической статистики

Первая задача математической статистики — указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики — разрабо­тать методы анализа статистических данных в зависи­мости от целей исследования. Сюда относятся:

а)   оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависи­мости случайной величины от одной или нескольких случайных величин и др.;

б)   проверка статистических гипотез о виде неизвест­ного распределения или о величине параметров распре­деления, вид которого известен.

Итак, задача математической статистики состоит в со­здании методов сбора и обработки статистических данных для получения научных и практических выводов.

 

Генеральная и выборочная совокупности

Пусть требуется изучить совокупность однород­ных объектов относительно некоторого качествен­ного или количественного признака, характе­ризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным — контролируе­мый размер детали.

Иногда проводят сплошное обследование, т. е. обсле­дуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование фи­зически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью или просто выборкой назы­вают совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n = 100.

Замечание. Часто генеральная совокупность содержит ко­нечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений, или для облегчения теоре­тических выводов, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправды­вается тем, что увеличение объема генеральной совокупности (доста­точно большого объема) практически не сказывается на результатах, обработки данных выборки.

При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бес­повторные.

Повторной называют выборку, при которой отобран­ный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того чтобы по данным выборки можно было до­статочно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции гене­ральной совокупности. Это требование коротко формули­руют так: выборка должна быть репрезентативной (пред­ставительной).

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют оди­наковую вероятность попасть в выборку.

Если объем генеральной совокупности достаточно ве­лик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бес­повторной выборками стирается; в предельном случае когда рассматривается бесконечная генеральная совокуп­ность, а выборка имеет конечный объем, это различие исчезает.

Способы отбора

На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:

1. Отбор, не требующий расчленения генеральной со­вокупности на части. Сюда относятся: а) простой слу­чайный бесповторный отбор; б) простой случайный по­вторный отбор.

2. Отбор, при котором генеральная совокупность раз­бивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.

Простым случайным называют такой отбор, при ко­тором объекты извлекают по одному из всей генераль­ной совокупности. Осуществить простой отбор можно различными способами. Например, для извлечения n объ­ектов из генеральной совокупности объема N поступают так: выписывают номера от 1 до N на карточках, которые тщательно перемешивают, и наугад вынимают одну кар­точку; объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют, т. е. карточки перемешивают, наугад вынимают одну из них и т. д. Так поступают n раз; в итоге получают простую случайную повторную выборку объема п.

Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.

При большом объеме генеральной совокупности опи­санный процесс оказывается очень трудоемким. В этом случае пользуются готовыми таблицами «случайных чисел», в которых числа расположены в случайном порядке. Для того чтобы отобрать, например, 50 объектов из пронуме­рованной генеральной совокупности, открывают любую страницу таблицы случайных чисел и выписывают под­ряд 50 чисел; в выборку попадают те объекты, номера которых совпадают с выписанными случайными числами. Если бы оказалось, что случайное число таблицы пре­вышает число N, то такое случайное число пропускают. При осуществлении бесповторной выборки случайные числа таблицы, уже встречавшиеся ранее, следует также пропустить.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части. Например, если детали изготовляют на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Типическим отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных типических частях генеральной совокупности. Например, если про­дукция изготовляется на нескольких машинах, среди которых есть более и менее изношенные, то здесь типи­ческий отбор целесообразен.

Механическим называют отбор, при котором генераль­ную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20% изготовленных станком деталей, то отби­рают каждую пятую деталь; если требуется отобрать 5% деталей, то отбирают каждую двадцатую деталь, и т. д. Следует указать, что иногда механический отбор может не обеспечить репрезентативности выборки. Например, если отбирают каждый двадцатый обтачиваемый валик, причем сразу же после отбора производят замену резца, то отобранными окажутся все валики, обточенные затуплен­ными резцами. В таком случае следует устранить совпа­дение ритма отбора с ритмом замены резца, для чего надо отбирать, скажем, каждый десятый валик из двад­цати обточенных.

Серийным называют отбор, при котором объекты от­бирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследова­нию. Например, если изделия изготовляются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков. Серийным отбором пользуются тогда, когда обследуемый признак колеблется в различных сериях незначитель­но.

Подчеркнем, что на практике часто применяется ком­бинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором выбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.

 

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ — n₂ раз, х_k — n_k раз и —объем выборки. Наблюдаемые значения x_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке,—вариа­ционным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки n_i/n = W_i — относи­тельными частотами.

Статистическим распределением выборки называют пе­речень вариант и соответствующих им частот или относи­тельных частот. Статистическое распределение можно за­дать также в виде последовательности интервалов и соответ­ствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Заметим, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математи­ческой статистике — соответствие между наблюдаемыми вариантами и их частотами, или относительными частотами.

Пример. Задано распределение частот выборки объема n = 20:

Написать распределение относительных частот.

Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:

 W₁ = 3/20 = 0,15, W₂= 10/20 = 0,50, W₃ = 7/20=0,35. Напишем распределение относительных частот:

Контроль: 0,15 + 0,50 + 0,35=1.

 

Эмпирическая функция распределения

Пусть известно статистическое распределение ча­стот количественного признака X. Введем обозначения: n_х—число наблюдений, при которых наблюдалось значение признака, меньшее х; n—общее число наблюдений (объем выборки). Ясно, что относительная частота события X < х равна n_х/n. Если х изменяется, то, вообще говоря, из­меняется и относительная частота, т. е. относительная частота n_х/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией рас­пределения выборки) называют функцию F*(х), опреде­ляющую для каждого значения х относительную частоту события X < х.

Итак, по определению.

где n_х—число вариант, меньших х; n — объем выборки.

Таким образом, для того чтобы найти, например, F*(x₂), надо число вариант, меньших х₂, разделить на объем выборки:

В отличие от эмпирической функции распределения выборки функцию распределения F(х) генеральной сово­купности называют теоретической функцией распределе­ния. Различие между эмпирической и теоретической функ­циями состоит в том, что теоретическая функция F (х) определяет вероятность события X < х, а эмпирическая функция F*(х) определяет относительную частоту этого же события.

Такое заключение подтверждается и тем, что F*(х) обладает всеми свойствами F(х). Действительно, из опре­деления функции F* (х) вытекают следующие ее свойства:

1) значения эмпирической функции принадлежат от­резку [0, 1];

2) F* (х) — неубывающая функция;

3) если х₁ — наименьшая варианта, то F*(x) = 0 при x≤ x₁; если x_k — наибольшая варианта, то F*(х) = 1 при x>x_k.

 

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

 

Пример. Построить эмпирическую функцию по данному распре­делению выборки:

варианты x_i  2   6  10

частоты  n_i 12 18 30

Решение. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая варианта равна 2, следовательно,

F*(x) = 0 при х ≤ 2.

Значение X < 6, а именно x₁ = 2, наблюдалось 12 раз, следовательно, F*(x)=12/60 =0,2 при 2 < x ≤ 6.

Значения X < 10, а именно х₁ = 2 и х₂ = 6, наблюдались 12 + 18 = 30 раз, следовательно, F* (х) = 30/60 = 0,5 при 6 < х ≤ 10. Так как x = 10 — наибольшая варианта, то F*(x)= 1 при х > 10.

Искомая эмпирическая функция

График этой функции изображен на рисунке

 

Полигон и гистограмма

Для наглядности строят различные графики ста­тистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х₁, n₁), (х₂; n₂), ..., (x_k; n_k). Для по­строения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат—соответствующие им частоты n_i. Точки (x_i; n_i) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х₁; W₁), (x₂; W₂), .... (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат—соответствующие им относительные ча­стоты W_i. Точки (х_i; W_i) соединяют отрезками прямых и получают полигон отно­сительных частот.

 

На рисунке изображен полигон относительных ча­стот следующего распре­деления:

X 1,5 3,5 5,5 7,5

W 0,1 0,2 0,4 0,3                 

В случае непрерывного признака целесо­образно строить гистограмму, для чего интервал, в ко­тором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала n_i — сумму частот вари­ант, попавших в i-й интервал.

Гистограммой ча­стот называют ступен­чатую фигуру, состоя­щую из прямоугольни­ков, основаниями кото­рых служат частичные интервалы длиною h, a высоты равны отношению n_i/h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/h.

Площадь i-ro частичного прямоугольника равна hn_i/h = n_i—сумме частот вариант i-ro интервала; следо­вательно, площадь гистограммы частот равна сумме всех частот, т. е. объему выборки.

На рисунке изображена гистограмма частот распреде­ления объема n =100, приведенного в таблице

 

Частичный интервал длиною h=5	Сумма частот вариант частичного интервала ni	Плотность частоты ni/h
5-10	4	0,8
10-15	6	1,2
15-20	16	3,2
20-25	36	7,2
25-30	24	4,8
35-40	10	2,0
45-50	4	0,8

 

Гистограммой относительных частот называют сту­пенчатую фигуру, состоящую из прямоугольников, осно­ваниями которых служат частичные интервалы длиною h, а высоты равны отношению W_i/h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i/h. Площадь i-ro частичного прямоугольника равна h W_i /h = W_i—относительной частоте вариант, попавших в i-й интервал. Следо­вательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице.

 

Контрольные вопросы.

1. Задачи математической статистики.

2. Что называется выборочной совокупностью?

3. Что называют генеральной совокупностью?

4. Что такое объем совокупности?

5. Что называют статистическим распределение выборки?

6. Что является эмпирической функцией распределения?

7. Свойства эмпирической функции распределения

8. Что называю полигоном частот?

9. Что называю полигоном относительных частот?

10. Что называю гистограммой частот?

11. Что называю гистограммой относительных частот?

12. Какая оценка называется несмещенной?

13. Какая оценка называется смещенной?

14. Какая оценка называется эффективной?

15. Какая оценка называется состоятельной?

16. Что называют генеральной средней?

17. Что называют выборочной средней?

18. Что называют генеральной дисперсией?

19. Что называют генеральным средним квадратическим отклонением?

20. Что называют выборочной дисперсией?

21. Написать формулу для вычисления выборочной дисперсии

22. Какую оценку называют интервальной?

23. Что такое надежность оценки?

24. Как находят доверительный интервал для оценки математического ожидания при известном σ?

25. Как находят доверительный интервал для оценки математического ожидания при неизвестном σ?

26. Как находят доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения?

27. Как пользоваться справочными таблицами?

 

Лекция № 9

Тема: «Статистические оценки параметров распределения»

План лекции

1. Статистические оценки параметров распределения

2. Несмещенные, состоятельные и эффективные оценки

3. Генеральная и выборочная средние

4. Генеральная и выборочная дисперсия

 

Статистические оценки параметров распределения

Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретичес­ких соображений удалось установить, какое именно рас­пределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распреде­ление. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормаль­но, то необходимо оценить (приближенно найти) матема­тическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормаль­ное распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки, например значения количественного при­знака х_1, х₂, .. ., х_n, полученные в результате n наблюде­ний (здесь и далее наблюдения предполагаются независимы­ми). Через эти данные и выражают оцениваемый параметр. Рассматривая х_1, х₂, .. ., х_n как независимые случайные величины Х₁, Х_{2, …,} Х_n, можно сказать, что найти статистическую оценку неизвестного параметра теоретиче­ского распределения — это значит найти функцию от наблюдаемых случайных величин, которая и дает при­ближенное значение оцениваемого параметра.

Итак, статистической оценкой неизвестного пара­метра теоретического распределения называют функцию от наблюдаемых случайных величин.

 

Несмещенные, эффективные и состоятельные оценки

Для того чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.

Несмещенной называют статистическую оценку Θ*, мате­матическое ожидание которой равно оцениваемому пара­метру Θ при любом объеме выборки, т. е.

М(Θ *) = Θ.

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако было бы ошибочным считать, что несмещенная оценка всегда дает хорошее приближение оцениваемого параметра. Действительно, возможные значения Θ* могут быть сильно рассеяны вокруг своего среднего значения, т. е. дисперсия D (Θ *) может быть значительной. В этом случае найденная по данным одной выборки оценка, на­пример Θ*₁, может оказаться весьма удаленной от среднего значения Θ *, а значит, и от самого оцениваемого пара­метра Θ; приняв  Θ*₁ в качестве приближенного значения Θ, мы допустили бы большую ошибку. Если же потребовать, чтобы дисперсия Θ* была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требование эффек­тивности.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую воз­можную дисперсию.

При рассмотрении выборок большого объема (n вели­ко!) к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, кото­рая при n→∞ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n→∞ стремится к нулю, то такая оценка оказы­вается и состоятельной.

 

Генеральная средняя

Пусть изучается дискретная генеральная совокуп­ность относительно количественного признака X.

Генеральной средней называют среднее арифметичес­кое значений признака генеральной совокупности.

Если все значения х_1, х₂, ..., x_n признака генераль­ной совокупности объема N различны, то  

Если же значения признака х_1, х₂, ..., x_n имеют соответственно частоты N_l, N₂, ..., N_k, причем N_l + N₂ + …+ N_k = N, то

т. е. генеральная средняя есть средняя взвешенная зна­чений признака с весами, равными соответствующим ча­стотам.

 

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена вы­борка объема n.

Выборочной средней называют среднее арифмети­ческое значение признака выборочной совокупности.

Если все значения х_1, х₂, ..., x_n признака выборки объема n различны, то  

Если же значения признака х_1, х₂, ..., x_n имеют соот­ветственно частоты n₁, n₂, ..., n_к, причем n₁+ n₂+ ...+ n_к = n, то

 или

т. е. выборочная средняя есть средняя взвешенная зна­чений признака с весами, равными соответствующим ча­стотам.

 

Генеральная дисперсия

Для того чтобы охарактеризовать рассеяние зна­чений количественного признака X генеральной совокуп­ности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифме­тическое квадратов отклонений значений признака гене­ральной совокупности от их среднего значения .

Если все значения х_1, х₂, ..., x_n признака генеральной совокупности объема N различны, то

Если же значения признака х_1, х₂, ..., x_n имеют соответственно частоты N_l, N₂, ..., N_k, причем N_l + N₂ + …+ N_k = N, то

т. е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствую­щим частотам.

Пример. Генеральная совокупность задана таблицей распреде­ления

х_i 2 4 5 6

N_i 8 9 10 3

Найти генеральную дисперсию.

Решение. Найдем генеральную среднюю

Найдем генеральную дисперсию

 

Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генераль­ной дисперсии:

Выборочная дисперсия

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения , вводят сводную характе­ристику— выборочную дисперсию.

Выборочной дисперсией D_в называют среднее арифме­тическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения х_1, х₂, ..., x_n признака генеральной совокупности объема n различны, то

Если же значения признака х_1, х₂, ..., x_n имеют соответственно частоты n_l, n₂, ..., n_k, причем n₁ + n₂ + …+ n_k = n, то

т. е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствую­щим частотам.

Пример. Выборочная совокупность задана таблицей распреде­ления

х_i   1 2 3 4

n_i 20 15 10 5

 

Найти выборочную дисперсию.

Решение. Найдем выборочную среднюю

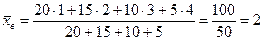
Найдем выборочную дисперсию

 

Кроме дисперсии для характеристики рассеяния зна­чений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии:

 

Оценка генеральной дисперсии по исправленной выборочной

Пусть из генеральной совокупности в результате n независимых наблюдений над количественным признаком Х извлечена повторная выборка объема n:

значения признака  х₁  х₂ ...  x_n

частоты                       n_l  n₂  ... n_k

При этом n₁ + n₂ + …+ n_k = n.

Требуется по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию D_г. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой D_г, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно

Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить D_в на дробь n/(n—1). Сделав это, получим исправленную дисперсию, которую обычно обозначают через s²:

Исправленная дисперсия является, конечно, несме­щенной оценкой генеральной дисперсии.

Итак, в качестве оценки генеральной дисперсии при­нимают исправленную дисперсию

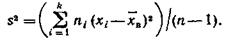
Для оценки же среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квад­ратному корню из исправленной дисперсии:

Подчеркнем, что s не является несмещенной оценкой; чтобы отразить этот факт, мы написали и будем писать далее так: «исправленное» среднее квадратическое откло­нение.

 

Контрольные вопросы.

1. Какие варианты называют равноотстоящими?

2. Какие варианты называют условными?

3. Что называют обычным эмпирическим моментом?

4. Что называют начальным эмпирическим моментом?

5. Что называют центральным эмпирическим моментом?

6. Что называют условным эмпирическим моментом?

7. Как выражаются обычные моменты через условные?

8. Как выражаются центральные моменты через условные?

9. Техника вычислений центральных моментов по условным с помощью метода произведений.

 

Лекция № 10

Тема: «Доверительные интервалы для оценки математического ожидания и среднего квадратического отклонения нормального распределения»

План лекции

1. Точность оценки, доверительная вероятность. Доверительный интервал

2. Доверительные интервалы для оценки математического ожидания

3. Доверительные интервалы для оценки среднего квадратического отклонения

 

Точность оценки, доверительная вероятность (надежность).

Доверительный интервал

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше,— точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интер­вальными оценками.

Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные оценки позволяют установить точность и надежность оценок

Пусть найденная по данным выборки статистическая характеристика Θ* служит оценкой неизвестного пара­метра Θ. Будем считать Θ постоянным числом (Θ может быть и случайной величиной). Ясно, что Θ * тем точнее определяет параметр Θ, чем меньше абсолютная величина разности | Θ — Θ*|. Другими словами, если δ >0 и | Θ — Θ*| < δ, то чем меньше δ, тем оценка точнее. Таким образом, положительное число δ характеризует точность оценки.

Однако статистические методы не позволяют катего­рически утверждать, что оценка Θ* удовлетворяет нера­венству | Θ — Θ* | < δ; можно лишь говорить о вероят­ности γ, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки в по Θ* называют вероятность γ, с которой осуществ­ляется неравенство | Θ — Θ *|< δ. Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надеж­ность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что | Θ — Θ*|< δ, равна γ

Р[|Θ - Θ*|< δ ] = γ.

Заменив неравенство | Θ — Θ *| < δ равносильным ему двой­ным неравенством —

-δ < Θ — Θ* < δ , или Θ *— δ < Θ < Θ* + δ, имеем

P[Θ*— δ < Θ < Θ* + δ ] = γ.

Это соотношение следует понимать так: вероятность того, что интервал

(Θ* —δ, Θ* + δ) заключает в себе (покры­вает) неизвестный параметр Θ, равна γ.

Доверительным называют интервал (Θ* —δ, Θ* + δ) который покрывает неизвестный параметр с заданной надежностью γ.

 

Доверительные интервалы для оценки математического ожидания нормального распределения при известном σ

Метод доверительных интервалов разработал амери­канский статистик Ю. Нейман, исходя из идей англий­ского статистика Р. Фишера.

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней . Поставим своей задачей найти доверительные интервалы, покрывающие параметр а с надежностью γ.

Параметры распределения таковы:

М( ) = а,  

Потребуем, чтобы выполнялось соотношение

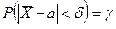
где γ — заданная надежность.

Пользуясь формулой )

заменив X на   и σ на , получим

, где , отсюда следует, что

Поэтому: ,

Приняв во внимание, что вероятность Р задана и равна γ, окончательно имеем

Смысл полученного соотношения таков: с надежностью γ можно утверждать, что доверительный интервал покрывает неизвестный параметр а; точность оценки

Итак, поставленная выше задача полностью решена. Укажем еще, что число t определяется из равенства Число t определяется из равенства 2∙Ф( t ) = γ, или Ф( t ) = γ/2; по таблице функции Лапласа находят аргумент t, которому соот­ветствует значение функции Лапласа, равное y/2.

Пример. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением σ = 3. Найти дове­рительные интервалы для оценки неизвестного математического ожи­дания а по выборочным средним , если объем выборки

n= 36 и задана надежность оценки γ = 0,95. 

Решение. Найдем t. Из соотношения 2∙Ф( t ) = 0,95 получим Ф( t ) = 0,475. По таблице значений функции Лапласа находим t = 1,96.

Найдем точность оценки:

Доверительный интервал таков: (  — 0,98;  +0,98). Например, если  = 4,1, то доверительный интервал имеет следующие доверительные границы:

— 0,98 = 4,1 — 0,98 = 3,12;  + 0,98 = 4,1+ 0,98 = 5,08.

Таким образом, значения неизвестного параметра а, согласую­щиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08.

 

Подчеркнем, что было бы ошибочным написать Р (3, 12 <а <5,08) = 0,95. Действительно, так как а — постоянная величина, то либо она заклю­чена в найденном интервале (тогда событие 3,12 < а < 5,08 досто­верно и его вероятность равна единице), либо в нем не заключена (в этом случае событие 3,12 < а < 5,08 невозможно и его вероят­ность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром; она связана лишь с границами доверительного интервала, которые, как уже было ука­зано, изменяются от выборки к выборке.

Поясним смысл, который имеет заданная надежность. Надеж­ность γ = 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интер­валы, в которых параметр действительно заключен; лишь в 5% слу­чаев он может выйти за границы доверительного интервала.

 

Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном σ

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ неизвестно. Требуется оце­нить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно вос­пользоваться результатами предыдущего параграфа, в ко­тором а предполагалось известным.

Оказывается, что по данным выборки можно построить случайную величину (ее возможные значения будем обозначать через t)

которая имеет распределение Стьюдента с k = n - 1 степенями свободы, здесь -выборочная средняя, S – «исправленное» среднее квадратическое отклонение, n – объем выборки.

Итак, пользуясь распределением Стьюдента, мы нашли доверительный интервал , по­крывающий неизвестный параметр а с надежностью γ.

Здесь случайные величины X и S заменены неслучайными величинами  и s, найденными по выборке.

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =16 найдены выбороч­ная средняя  = 20,2 и «исправленное» среднее квадратическое откло­нение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем t_γ. Пользуясь таблицей приложения 3, по γ = 0,95 и n=16 находим  t_γ=2,13.

Найдем доверительные границы:

20,2 — 2,13 ∙ 0,8/  =19,774

20,2 + 2,13 ∙ 0,8/  = 20,626.

Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626.

 

Замечание. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к оценке мате­матического ожидания (при неизвестном σ) при помощи доверитель­ного интервала

 

Доверительные интервалы для оценки среднего квадратического отклонения о нормального распределения

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое откло­нение σ по «исправленному» выборочному среднему квадратическому отклонению s. Поставим перед собой задачу найти доверительные интервалы, покрывающие параметр σ с заданной надежностью γ.

Потребуем, чтобы выполнялось соотношение

Доверительный интервал, покрывающий параметр σ с заданной надежностью γ имеет вид

Практически для отыскания q пользуются таблицей из приложения 4 по заданным n и γ

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено «исправ­ленное» среднее квадратическое отклонение s=0,8. Найти доверитель­ный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.

Решение. По таблице приложения 4 по данным γ = 0,95 и n = 25 найдем q = 0,32.

Искомый доверительный интервал таков:

0,8 (1—0,32) < а < 0,8 (1+0,32), или 0,544 < а < 1,056.

 

Контрольные вопросы.

1. Какие существуют виды зависимостей?

2. Что называют статистической зависимостью?

3. Что называют корреляционной зависимостью?

4. Что называют условным средним?

5. Какое уравнение называют выборочным уравнением регрессии?

6. Какую функцию называют выборочной регрессией?

7. Что является выборочной линией регрессии?

8. Что называют выборочным коэффициентом регрессии?

9. В чем заключается метод наименьших квадратов?

10. Как пользоваться справочными таблицами?

 

Лекция № 11

Тема: «Методы расчета сводных характеристик выборки»

План лекции

1. Условные варианты. Обычные, начальные и центральные эмпирические моменты

2. Условные эмпирические моменты.

3. Метод произведений для вычисления выборочных средней и дисперсии

 

Условные варианты

Предположим, что варианты выборки расположены в возрастающем порядке, т.е. в виде вариационного ряда.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h. Условными называют варианты, определяемые равенством

u_i = (x_i – C)/h

где С – ложный нуль (новое начало отсчета), h – шаг, т.е. разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба)

 

Обычные,  начальные и центральные эмпирические моменты

Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, опреде­ления которых аналогичны определениям соответствующих теоретических моментов. В от­личие от теоретических эмпирические моменты вычисляют по данным наблюдений.

Обычным эмпирическим моментом порядка k называют среднее значение k-x степеней разностей х_i—С:

где x_i—наблюдаемая варианта, n_i—частота варианты, - объем выборки, С—произвольное постоянное число (ложный нуль).

Начальным эмпирическим моментом порядка k назы­вают обычный момент порядка k при С — О

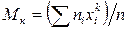
В частности,

т. е. начальный эмпирический момент первого порядка равен выборочной средней.

Центральным эмпирическим моментом порядка k на­зывают обычный момент порядка k при

В частности,

т. е. центральный эмпирический момент второго порядка равен выборочной дисперсии.

 

Условные эмпирические моменты. Отыскание центральных моментов по условным

Вычисление центральных моментов требует до­вольно громоздких вычислений. Чтобы упростить рас­четы, заменяют первоначальные варианты условными.

Условным эмпирическим моментом порядка k называ­ют начальный момент порядка ft, вычисленный для условных вариант:

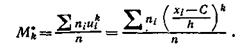 I

Отсюда

 

Таким образом, для того чтобы найти выборочную среднюю достаточно вычислить условный момент первого Iпорядка, умножить его на h и к результату прибавить ложный нуль С.

 Выразим обычные моменты через условные:

Отсюда

Таким образом, для того чтобы найти обычный момент порядка к, достаточно условный момент того же порядка умножить на h^k.

Формула для вычисления выборочной дисперсии по условным моментам первого и второго порядков

 

Техника вычислений центральных моментов по условным описана далее.

 

Метод произведений для вычисления выборочных средней и дисперсии

Метод произведений дает удобный способ вычис­ления условных моментов различных порядков вариаци­онного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти интересующие нас начальные и центральные эмпирические моменты. В част­ности, методом произведений удобно вычислять выбороч­ную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется так:

1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;

2) во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки n) помещают в нижнюю клетку столбца;

3) в третий столбец записывают условные варианты x_i= (x_i—C)/h, причем в качестве ложного нуля С выбирают варианту, которая расположена примерно в сере­дине вариационного ряда, и полагают h равным разности между любыми двумя соседними вариантами; практически же третий столбец заполняется так: в клетке строки, содержащей выбранный ложный нуль, пишут 0; в клет­ках над нулем пишут последовательно —1, —2, —3 и т.д., а под нулем—1, 2, 3 и т.д.;

4) умножают частоты на условные варианты и запи­сывают их произведения n_iu_i в четвертый столбец; сло­жив все полученные числа, их сумму  помещают в нижнюю клетку столбца;

5) умножают частоты на квадраты условных вариант и записывают их произведения n_iu_i ² в пятый столбец; сложив все полученные числа, их сумму поме­щают в нижнюю клетку столбца;

6) умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произве­дения  n_i ( u_i + 1)² в шестой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца.

После того как расчетная таблица заполнена и про­верена правильность вычислений, вычисляют условные моменты:

Наконец, вычисляют выборочные среднюю и диспер­сию по формулам:

Пример. Найти методом произведений выборочные среднюю и дисперсию следующего статистического распределения:

варианты 10,2   10,4 10,6 10,8 11,0 11,2 11,4 11,6 11,8 12,0

частоты  2    3  8  13 25  20 12 10  6    1

 

Решение. Составим расчетную таблицу, для чего:

1) запишем варианты в первый столбец;

2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца;

3) в качестве ложного нуля выберем варианту 11,0 (эта вариан­та расположена примерно в середине вариационного ряда); в клетке третьего столбца, которая принадлежит строке, содержащей выбран­ный ложный нуль, пишем 0; над нулем записываем последовательно —1, —2, —3, —4, а под нулем — 1, 2, 3, 4, 5;

4) произведения частот на условные варианты записываем в четвертый столбец; отдельно находим сумму (—46) отрицательных и от­ дельно сумму (103) положительных чисел; сложив эти числа, их сумму (57) помещаем в нижнюю клетку столбца;

5) произведения частот на квадраты условных вариант запишем в пятый столбец; сумму чисел столбца (383) помещаем в нижнюю клетку столбца;

6) произведения частот на квадраты условных вариант, увели­ченных на единицу, запишем в шестой контрольный столбец; сумму (597) чисел столбца помещаем в нижнюю клетку столбца.

В итоге получим расчетную таблицу.

Вычисления произведены правильно.

 

Вычислим условные моменты первого и второго порядков:

 

Найдем шаг: h= 10,4— 10,2 = 0,2.

Вычислим искомые выборочные среднюю и дисперсию:

 

 

Контрольные вопросы.

1. Какую зависимость называют статистической?

2. Какую зависимость называют корреляционной?

3. Что называют условным средним?

4. В качестве каких оценок принимают условные средние?

5. Какое уравнение называют выборочным уравнением регрессии?

6. Какую функцию называют выборочной регрессией?

7. Что называют выборочной линией регрессии?

8. Что называют выборочным коэффициентом регрессии?

9. Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?

10. Как пользоваться справочными таблицами?

Лекция № 12

Тема: «Виды зависимостей. Выборочный коэффициент корреляции и уравнение регрессии»

План лекции

1. Функциональная, статистическая и корреляционная зависимости

2. Выборочные уравнения регрессии

3. Отыскание параметров выборочного уравнения прямой линии среднеквадратичной регрессии по не сгруппированным данным

 

Функциональная, статистическая и корреляционная зависимости

Во многих задачах требуется установить и оце­нить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X.

Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Строгая функциональная зависимость реализуется ред­ко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин (под «общими» здесь подразумеваются такие факторы, которые воздействуют и на У и на X). В этом случае возникает статистическая зависимость.

Например, если Y зависит от случайных факторов Z₁, Z₂, V_l, V₂, a X зависит от случайных факторов Z_l, Z₂, U₁, то между Y и Х имеется статистическая зависимость, так как среди случайных факторов есть общие, а имен­но: Z₁ и Z₂.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распреде­ления другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае ста­тистическую зависимость называют корреляционной.

Приведем пример случайной величины Y, которая не связана с величиной X функционально, а связана кор­реляционно. Пусть Y—урожай зерна, X—количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, т. е. Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, как показы­вает опыт, средний урожай является функцией от количе­ства удобрений, т. е. Y связан с X корреляционной зависи­мостью.

 

Условные средние

В качестве оценок условных математических ожиданий принимают условные сред­ние, которые находят по данным наблюдений (по выборке).

Условным средним называют среднее арифметиче­ское наблюдавшихся значений Y, соответствующих X = х. Например, если при x₁ = 2 величина Y приняла значе­ния у₁ = 5, у₂= 6, у₃ =10, то условное среднее = (5 + 6+10)/3 = 7.

Аналогично определяется условное среднее .

Условным средним называют среднее арифметическое наблюдавшихся значений X, соответствующих Y = y.

 

Выборочные уравнения регрессии

Услов­ное среднее  функция от х; обозначив эту функ­цию через f*(x), получим уравнение

Это уравнение называют выборочным уравнением регрес­сии Y на X; функцию f* (х) называют выборочной регрес­сией Y на X, а ее график—выборочной линией регрес­сии Y на X. Аналогично уравнение

называют выборочным уравнением регрессии X на Y; функ­цию φ* (у) называют выборочной регрессией X на Y, а ее график—выборочной линией регрессии X на Y.

 

Как найти по данным наблюдений параметры функ­ций f*(x) и φ* (у), если вид их известен? Как оценить силу (тесноту) связи между величинами X и Y и устано­вить, коррелированны ли эти величины? Ответы на эти вопросы изложены ниже.

 

Отыскание параметров выборочного уравнения Прямой линии среднеквадратичной регрессии по несгруппированным данным

Пусть изучается система количественных приз­наков (X, Y). В результате n независимых опытов полу­чены n пар чисел (x_1, y₁), (x₂, у₂), ..., (х_n, у_n).

Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии. Для определенности будем искать уравнение

 = kx + b

регрессии Y на X.

Поскольку различные значения х признака X и соот­ветствующие им значения у признака Y наблюдались по одному разу, то группировать данные нет необходи­мости. Также нет надобности использовать понятие услов­ной средней, поэтому искомое уравнение можно записать так:

y = kx - b.

Угловой коэффициент прямой линии регрессии У на X называют выборочным коэффициентом регрессии У на X и обозначают через ρ_ух

Итак, будем искать выборочное уравнение прямой линии регрессии У на Х вида

             (*)

Подберем параметры ρ_ух и b так, чтобы точки (x_1, y₁), (x₂, у₂), ..., (х_n, у_n), построенные по данным наб­людений, на плоскости хОу лежали как можно ближе к прямой (*). Уточним смысл этого требования. Назовем отклонением разность

Y_i—у_i, (i=1, 2,…, n),

где Y_i — вычисленная по уравнению (*) ордината, соответ­ствующая наблюдаемому значению x_i; у_i — наблюдаемая ордината, соответствующая х_i.

Подберем параметры ρ_ух и b так, чтобы сумма квад­ратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каж­дое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция F этих параметров (временно вместо ρ_ух будем писать ρ):

или

Для отыскания минимума приравняем нулю соответству­ющие частные производные:

Выполнив элементарные преобразования, получим си­стему двух линейных уравнений относительно ρ и b. Решив эту систему, найдем искомые параметры:

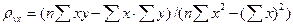
Аналогично можно найти выборочное уравнение пря­мой линии регрессии X на Y:

где ρ_хy — выборочный коэффициент регрессии X на У.

 

Пример. Найти выборочное уравнение прямой линии регрессии У на X по данным n = 5 наблюдений:

 

х 1,00 1,50 3,00 4,50 5,00

у 1,25 1,40 1,50 1,75 2,25

Решение. Составим расчетную таблицу

 

 

Найдем искомые параметры, для чего подставим вычисленные по таблице суммы в соотношения:

р_ху = (5 ∙ 26,975— 15 ∙ 8,15)/(5 ∙ 57,5—15²) = 0,202;

b = (57,5 ∙ 8,15—15 ∙ 26,975)/62,5= 1,024.

Напишем искомое уравнение регрессии:

Y = 0,202x - 1,024

Для того чтобы получить представление, насколько хорошо вы­численные по этому уравнению значения Y_i согласуются с наблюдае­мыми значениями у_i, найдем отклонения

У_i - y_i. Результаты вычис­лений приведены в таблице

 

Как видно из таблицы, не все отклонения достаточно малы. Это объясняется малым числом наблюдений.

 

Контрольные вопросы.

1. Какую зависимость называют статистической?

2. Какую зависимость называют корреляционной?

3. Что называют условным средним?

4. В качестве каких оценок принимают условные средние?

5. Какое уравнение называют выборочным уравнением регрессии?

6. Какую функцию называют выборочной регрессией?

7. Что называют выборочной линией регрессии?

8. Что называют выборочным коэффициентом регрессии?

9. Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?

10. Как пользоваться справочными таблицами?

11. Какие варианты называют равноотстоящими?

12. Какие варианты называют условными?

13. Как находятся параметры выборочного уравнения прямой линии среднеквадратичной регрессии по не сгруппированным данным?

 

Лекция № 13

Тема: «Методика расчетов выборочного коэффициента корреляции и уравнения прямой линии регрессии»

План лекции

1. Параметры выборочного уравнения прямой линии регрессии по сгруппированным данным

2. Выборочный коэффициент корреляции

3. Методика вычисления выборочного коэффициента корреляции

4. Нахождение выборочного уравнения прямой линии регрессии

 

Параметры выборочного уравнения прямой линии регрессии по сгруппированным данным

Допустим, что получено большое число данных (практически для удовлетворительной оценки искомых параметров должно быть хотя бы 50 наблюдений), среди них есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы.

Введя новую величину – выборочный коэффициент корреляции, напишем уравнение регрессии в другом виде

 

, или

Аналогично, выборочное уравнение прямой линии регрессии X на Y вида

Выборочный коэффициент корреляции

Выбо­рочный коэффициент корреляции определяется равенством

где х, у—варианты (наблюдавшиеся значения) признаков X и Y; n_ху — частота пары вариант (х, у); n — объем выборки (сумма всех частот); , —выборочные средние квадратические отклонения; , —выборочные средние.

Известно, что если величины Y и X независимы, то коэффициент корреляции r =0; если r = ± 1, то Y и X связаны линейной функциональной зависимостью. Отсюда следует, что коэффициент корреляции r измеряет силу (тесноту) линейной связи между У и X.

Выборочный коэффициент корреляции r _в является оценкой коэффициента корреляции r генеральной сово­купности и поэтому также служит для измерения линей­ной связи между величинами—количественными призна­ками Y и X. Допустим, что выборочный коэффициент корреляции, найденный по выборке, оказался отличным от нуля. Так как выборка отобрана случайно, то отсюда еще нельзя заключить, что коэффициент корреляции ге­неральной совокупности также отличен от нуля. Возни­кает необходимость проверить гипотезу о значимости (существенности) выборочного коэффициента корреляции (или, что то же, о равенстве нулю коэффициента корре­ляции генеральной совокупности). Если гипотеза о равен­стве нулю генерального коэффициента корреляции будет отвергнута, то выборочный коэффициент корреляции зна­чим, а величины X и Y коррелированны; если гипотеза принята, то выборочный коэффициент корреляции незна­чим, а величины X и Y не коррелированны.

 

Замечание. Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии. Действительно, перемножив левые и правые части равенств, получим

Отсюда

Знак при радикале совпадать со знаком коэффициентов регрессии.

 

 

Методика вычисления выборочного коэффициента корреляции

Пусть требуется по данным корреляционной таблицы вычислить выборочный коэффициент корреляции. Можно значительно упростить расчет, если перейти к условным вариантам (при этом величина r_в не изменится)

u_i =( x_i – C ₁ )/ h ₁ и v_i = ( y_j – C ₂ )/ h ₂

В этом случае выборочный коэффициент корреляции вы­числяют по формуле

Величины , , , 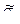можно найти методом произве­дений, а при малом числе данных — непосредственно исходя из определений этих величин. Остается указать способ вычисления , где n_uv — частота пары условных вариант (u , v).

Можно доказать, что справедливы формулы:

Для контроля целесообразно выполнить расчеты по обеим формулам и сравнить результаты; их совпадение свидетельствует о правильности вычислений.

Покажем на примере, как пользоваться приведенными формулами.

 

Пример 1. Вычислить по данным корреляционной таблицы 1

 

Таблица 1

 

 

 

Решение. Перейдем к условным вариантам: u_i =( x_i – C ₁ )/ h ₁ = (x_i - 40)/10 (в качестве ложного нуля С₁ взята варианта x =40, расположенная примерно в середине вариационного ряда; шаг h ₁ равен разности между двумя соседними вариантами: 20—10=10) и v_i = ( y_j – C ₂ )/ h ₂ = (y_j — 35)/10 (в качестве ложного нуля С₂ взята варианта y = 35, расположенная в середине вариационного ряда; шаг h₂ равен разности между двумя соседними вариантами: 25 — 15=10).

Составим корреляционную таблицу в условных вариантах. Прак­тически это делают так: в первом столбце вместо ложного нуля С₂ (варианты 35) пишут 0; над нулем последовательно записывают —1, - 2; под нулем пишут 1, 2. В первой строке вместо ложного нуля С₁ (варианты 40) пишут 0; слева от нуля последовательно записывают —1, —2, —3; справа от нуля пишут 1, 2. Все остальные данные переписывают из первоначальной корреляционной таблицы. В итоге получим корреляционную таблицу2 в условных вариантах.

 

 

Таблица 2

 

 

 

Теперь для вычисления искомой суммы составим рас­четную таблицу3. Пояснения к составлению таблицы 3:

 1. В каждой клетке, в которой частота n_uv ≠ 0, записывают в правом верхнем углу произведение частоты n_uv на варианту и. Например, в правых верхних углах клеток первой строки записаны произведения: 5 ∙ (—3) = —15; 7 ∙ (—2)=—14.

2. Складывают все числа, помещенные в правых верхних углах клеток одной строки, и их сумму записывают в клетку этой же строки столбца U. Например, для первой строки U =—15 + (—14) =—29.

3. Умножают варианту v на U и полученное произведение записывают в последнюю клетку той же строки, т. е. в клетку столбца vU. Например, в первой строке таблицы v = —2, U =—29; следовательно,  vU = (—2) ∙ (—29) = 58.

4. Наконец, сложив все числа столбца vU, получают сумму , которая равна искомой сумме . Например, для таблицы 3 имеем   = 169; следовательно, искомая сумма = 169.

Таблица 3

 

Для контроля аналогичные вычисления производят по столбцам: произведения n_uvv записывают в левый нижний угол клетки, содер­жащей частоту n_uv ≠ 0; все числа, помещенные в левых нижних углах клеток одного столбца, складывают и их сумму записывают в строку V; далее умножают каждую варианту и на V и результат записывают в клетках последней строки.

Наконец, сложив все числа последней строки, получают сумму , которая также равна искомой сумме . Например, для таблицы 3 имеем = 169; следовательно, = 169.

Пример 2. Вычислить выборочные коэффициент корреляции по данным корреляционной таблицы 1.

Решение. Перейдя к условным вариантам, получим корреля­ционную таблицу 2. Величины , , , можно вычислить методом произведений; однако, поскольку числа и _i, v_i малы, вычислим , , исходя из определения средней, а , —используя формулы 

Найдем , :

                    [5∙(-3) + 27∙(-2) + 63∙(-1)+29∙1 + +9∙2]/200 = — 0,425;

[12∙(—2) + 43∙(— 1)+ 47∙1 +19∙2]/200=0,09.

Вычислим вспомогательную величину и², а затем σ _u

(5∙9 + 27∙4 + 63∙1+29∙1 +9∙4)/200= 1,405

Аналогично получим  = 1,209.

Найдем искомый выборочный коэффициент корреляции, учитывая, что ранее уже вычислена сумма = 169:

 [169—200∙(—0,425) ∙ 0,09]/(200 ∙ 1,106 ∙ 1,209) = 0,603.

Итак, r_в = 0,603.

 

Отыскание выборочного уравнения прямой линии регрессии

Поскольку при нахождении r_в уже вычислены , , , , то целесообразно пользоваться формулами:

; ; ;

Пример 3. Найти выборочное уравнение прямой линии регрессии Y на X по данным корреляционной таблицы 1.

Решение. Напишем искомое уравнение в общем виде:

 

Коэффициент корреляции уже вычислен. Остается найти , , , :

 = -0,425 ∙ 10+40 = 35,75

= 0,09 ∙ 10 + 35 = 35,9;

= 1,106 ∙ 10 = 11,06;

= 1,209 ∙ 10= 12,09.

Подставив найденные величины, получим искомое уравнение

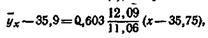
или окончательно

Сравним условные средние, вычисленные: а) по этому уравнению; б) по данным корреляционной таблицы 1. Например, при х = 30:

а)   ₃₀= О,659 ∙ 30+12,34 = 32,11;

б)   ₃₀ = (23 ∙ 25 + ЗО ∙ 35+1О ∙ 45)/63 = 32,94.

Как видим, согласование расчетного и наблюдаемого условных средних — удовлетворительное.

 

Контрольные вопросы.

1. Какую зависимость называют статистической?

2. Какую зависимость называют корреляционной?

3. Что называют условным средним?

4. В качестве каких оценок принимают условные средние?

5. Какое уравнение называют выборочным уравнением регрессии?

6. Какую функцию называют выборочной регрессией?

7. Что называют выборочной линией регрессии?

8. Что называют выборочным коэффициентом регрессии?

9. Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?

10. Как пользоваться справочными таблицами?

11. Какие варианты называют равноотстоящими?

12. Какие варианты называют условными?

13. Как находятся параметры выборочного уравнения прямой линии регрессии по сгруппированным данным?

14. Методика вычисления выборочного коэффициента корреляции

15. Методика расчета выборочного уравнения прямой линии регрессии

 

 

---

Дата добавления: 2019-09-13; просмотров: 876; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!